
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Центр ваги твердого тіла. На кожну k-ту частину тіла, яке знаходиться біля земної поверхні, діє направлена вертикально вниз сила
На кожну k -ту частину тіла, яке знаходиться біля земної поверхні, діє направлена вертикально вниз сила 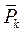 , яка названа силою ваги.
, яка названа силою ваги.
У дійсності сила ваги складається з окремих складових, які прикладені до окремих частин тіла, та є системою збіжних сил, бо лінії дії цих сил перетинаються в одній точці – у центрі Землі. Для тіл, розміри яких малі порівняно з радіусом Землі, сили ваги 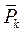 усіх частинок можна вважати паралельними між собою й такими, що зберігають постійну величину при будь-яких поворотах тіла. Поле сили ваги, у якому виконуються ці дві умови, називається однорідним полем сили ваги.
усіх частинок можна вважати паралельними між собою й такими, що зберігають постійну величину при будь-яких поворотах тіла. Поле сили ваги, у якому виконуються ці дві умови, називається однорідним полем сили ваги.
Позначимо через 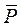 рівнодіючу паралельних сил ваги
рівнодіючу паралельних сил ваги 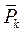 (k =1,2,3,..., n). Модуль рівнодіючої дорівнює силі ваги тіла і визначається за формулою:
(k =1,2,3,..., n). Модуль рівнодіючої дорівнює силі ваги тіла і визначається за формулою:
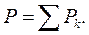
Рівнодіюча 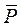 паралельних сил ваги
паралельних сил ваги 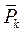 при будь-яких положеннях тіла проходить через одну й ту ж незмінно пов’язану з тілом точку С, що є центром паралельних сил ваги (k =1,2,3,..., n). Ця точка називається центром ваги тіла.
при будь-яких положеннях тіла проходить через одну й ту ж незмінно пов’язану з тілом точку С, що є центром паралельних сил ваги (k =1,2,3,..., n). Ця точка називається центром ваги тіла.
Центр ваги твердого тіла має таку властивість, що через нього проходить лінія дії рівнодіючої паралельних сил ваги окремих його частинок незалежно від розташування тіла в просторі. Ця властивість дозволяє експериментально визначити центр ваги неоднорідного тіла складної конфігурації згідно з правилом: достатньо підвісити тіло на нитці в деякій точці та побудувати продовження нитки в тіло. Потім підвісити тіло на нитці в іншій точці й також побудувати продовження нитки в тілі. Тоді перетин побудованих ліній визначить центр ваги цього тіла.
Для визначення координат центру ваги тіла використовують такі формули:
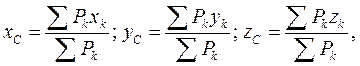
де 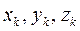 - координати точок прикладання сил ваги
- координати точок прикладання сил ваги 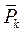 частинок тіла.
частинок тіла.
Якщо позначити масу тіла через 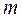 , а маси окремих частинок – через
, а маси окремих частинок – через 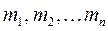 , то:
, то:
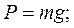
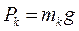 (k =1,2,3,..., n),
(k =1,2,3,..., n),
де g – прискорення сили ваги.
Підставимо ці значення у попередні формули і одержимо:
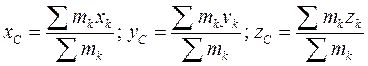 .
.
Точка, координати якої визначаються цими формулами, називається центром мас або центром інерції тіла. Центр мас характеризує розподіл маси в тілі.
Якщо тіло однорідне, то координати його центру ваги визначаються так:
 (1)
(1)
де 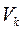 - об’єм k -тої частинки тіла.
- об’єм k -тої частинки тіла.
Якщо тіло є однорідною тонкою пластинкою постійної товщини, то
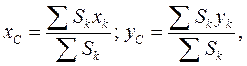 (2)
(2)
де 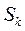 - площі окремих частин пластинки.
- площі окремих частин пластинки.
Точку С, координати якої визначаються такими формулами, називають центром ваги площі.
Для координат центру ваги лінії формули такі:
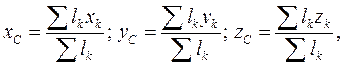 (3)
(3)
де 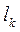 - довжини окремих частин лінії.
- довжини окремих частин лінії.
Розглянемо методи визначення координат центрів ваги тіл.
1. Метод симетрії. Якщо однорідне тіло має площину, вісь або центр симетрії, то центр ваги цього тіла лежить відповідно або в площині, або на осі, або в центрі симетрії.
Наслідки:
а) центр ваги відрізка матеріальної прямої лінії лежить у його середині;
б) центр ваги круглого кільця, круглої або прямокутної пластинки, площі правильного многокутника чи еліпса, об’єму прямокутного паралелепіпеда, кулі та інших тіл, які мають центр симетрії, лежить у їх геометричних центрах (у центрах симетрії).
2. Метод розбивання. Цей метод застосовують для визначення положення центру ваги тіл складної форми. Загальний метод визначення положення центру ваги полягає в тому, що тіло розбивають на скінчене число частин більш простої геометричної форми, для яких центр ваги легко знайти. Тоді координати центру ваги всього тіла визначають за відповідними формулами (1), (2) або (3), приймаючи: 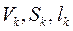 - відповідно об’єми, площі та довжини окремих частин, на які розбивають дане тіло, плоску фігуру або лінію;
- відповідно об’єми, площі та довжини окремих частин, на які розбивають дане тіло, плоску фігуру або лінію; 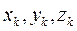 - координати центрів ваги цих частин.
- координати центрів ваги цих частин.
3. Метод доповнення. Цей метод є окремим випадком методу розбивання. Він застосовується до тіл, які мають вирізи, якщо центри ваги тіла без вирізів та вирізаних частин відомі.
Позначимо площу плоского тіла без вирізів через 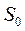 , площі вирізаних частин - через
, площі вирізаних частин - через 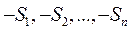 , а координати їх центрів ваги - через
, а координати їх центрів ваги - через 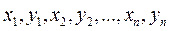 . Тоді координати центру ваги плоского тіла з вирізами обчислюються за такими формулами:
. Тоді координати центру ваги плоского тіла з вирізами обчислюються за такими формулами:
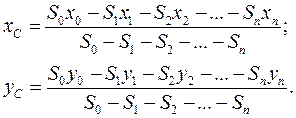

Аналогічно визначаються координати центру ваги об’ємного тіла з вирізами.
4. Метод інтегрування. Якщо тіло не можна розбити на частини, положення центрів ваги яких відоме, то тіло розбивають на елементарні об’єми. У такому випадку координати центру ваги визначають за формулами:
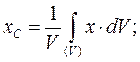
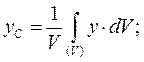
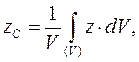
де 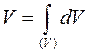 - об’єм тіла, що розглядається; інтеграли поширені на об’єм всього тіла.
- об’єм тіла, що розглядається; інтеграли поширені на об’єм всього тіла.
Для плоскої фігури положення центру ваги визначається за формулами:
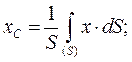
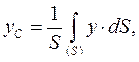
де 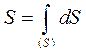 - площа фігури, що розглядається; інтеграли поширюються на площу всієї фігури.
- площа фігури, що розглядається; інтеграли поширюються на площу всієї фігури.
Координати центру ваги матеріальної лінії визначають так:
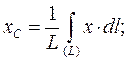
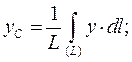
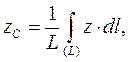
де 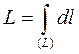 - довжина лінії, що розглядається.
- довжина лінії, що розглядається.
Визначимо положення центрів ваги деяких ліній, площ і об’ємів.
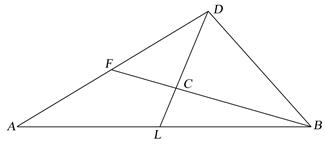 Центр ваги площі трикутника. Центр ваги площі трикутника лежить у точці перетину його медіан. При цьому, як відомо з геометрії,
Центр ваги площі трикутника. Центр ваги площі трикутника лежить у точці перетину його медіан. При цьому, як відомо з геометрії,
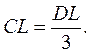
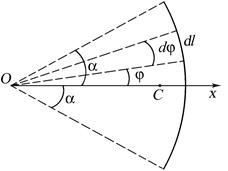 Центр ваги дуги кола. Центр ваги дуги кола лежить на осі її симетрії на відстані ОС від центру кола:
Центр ваги дуги кола. Центр ваги дуги кола лежить на осі її симетрії на відстані ОС від центру кола:
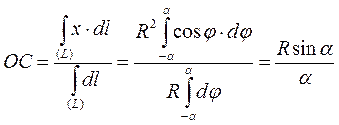 ,
,
де кут 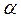 вимірюється в радіанах.
вимірюється в радіанах.
Для дуги півкола 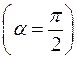 :
: 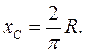
Центр ваги площі кругового сектора. Центр ваги площі кругового сектора лежить на його осі симетрії на відстані хС від центру, яка дорівнює
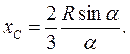
Для сектора у вигляді півкола 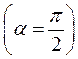 :
: 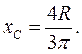
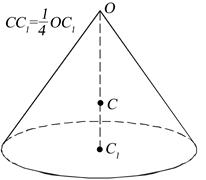
Центр ваги об’єму конуса та піраміди. Центр ваги об’єму однорідного круглого конуса лежить на відрізку, що з’єднує вершину конуса з центром ваги його основи, на відстані однієї чверті довжини цього відрізка від центру ваги основи конуса. Це справедливо також для однорідної піраміди.
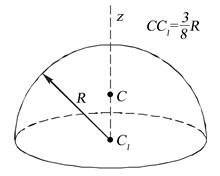 Центр ваги об’єму півкулі. Центр ваги об’єму півкулі лежить на осі симетрії та знаходиться на відстані
Центр ваги об’єму півкулі. Центр ваги об’єму півкулі лежить на осі симетрії та знаходиться на відстані
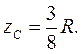
Date: 2015-07-27; view: 1096; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |