Математическая модель

Прелесть прикладной математики заключается в том, что она в первую очередь работает с моделями физических объектов и процессов, а не с реальным железом. Математическая модель — всегда некоторое приближение реальности. Вопрос об определении степени точности обычно первоочередной при решении задач, здесь важно не кидаться в границы возможного. Использовать полные уравнения баллистики с целью приблизительной оценки, допустим, дальности — одна крайность. Недосмотреть за склонностью небольшого узла к автоколебательным процессам — пример второй крайности. И, на самом деле, не всегда можно понять, что хуже. В первом случае легко потратить огромное количество машинного времени и получить в итоге неверный результат по причине того, что тонкие параметры брали примерно. Во втором — можно просто потерять управляемость ракеты в случайный момент времени.

Если же грамотно выбрать степень сложности и точности математической модели, то, учитывая нынешнее развитие компьютерной техники, мы получаем в руки замечательное оружие, убойная сила которого заключается в безболезненном для реальных объектов прогнозировании результата наших действий. Так, например, душе и кошельку куда проще увидеть на экране зашкаливание каких-то параметров во время моделирования, чем, сидя на наблюдательном посту, глядеть за аварией реальной машины, которая стоит больших денег и упорного труда. Кроме того, это дает замечательное пространство экспериментам, ведь ничего не стоит (кроме электричества и времени) поменять пару параметров с целью удовлетворить любопытный порыв «а будет ли лучше?».

Однако, как уже говорилось, какова бы не была по сложности модель, это обязательно будет именно упрощением реальности, по двум основным причинам: не все процессы в принципе детерминированно описательны (прибегаем к вероятностным оценкам); некоторые точные модели приводят к решительной невозможности с этой моделью работать по причине безумного размера формул и годовых трат по моделированию. К разговору о точности мы еще вернемся, а пока начнем построение математической модели ракеты в общем виде.

Общая идея — ракету представляем движением центра масс и вращения вокруг нее. В основном мы будем обращать внимание именно на центр масс, рассматривая вращательные моменты лишь косвенно.

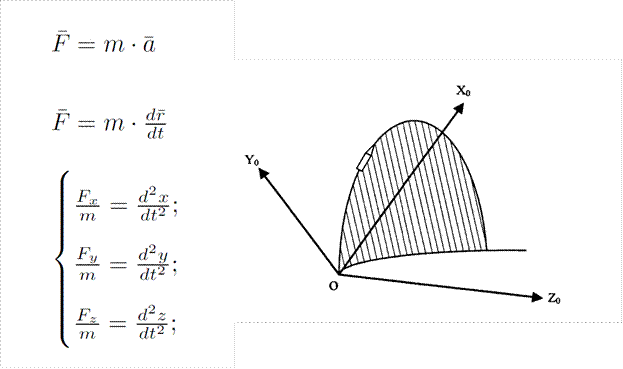
Математическая модель центра масс ракеты, как и большинства динамических систем, базируется на известном еще со школы втором законе Ньютона — сила есть масса на ускорение. Умные дяди в университетах говорят иначе — вторая производная по времени закона движения есть сила делить на массу. Производная какой-то величины — это скорость (закон) ее изменения. Вторая производная — это производная производной, т.е. это скорость скорости изменения величины. А скорость скорости — это ускорение. Выясняем, что дяди оказались правы и идем дальше.

Теперь можно сказать солидней — мы получили дифференциальное уравнение второго порядка. Однако, так уж сложилось, это «общее» движение проще рассмотреть, разделив его на три, т.е. разложить его на сумму движений в трех независимых направлениях. Так будет легче и визуально, и математически. Что имеем? Систему из трех дифференциальных уравнений второго порядка. На самом деле, все еще не очень вкусно. Всякому математику-управленцу известно, что самая вкусная система диффуров — это система первого порядка, ибо все основные методы теории оптимального управления базируются именно на них. Поэтому сделаем простую замену переменных — вторую производную закона движения заменим на первую производную закона скорости, а первую производную закона движения прировняем к просто закону скорости. Итого — уравнений аж 6, однако в самом прелестном виде.

Решить эти уравнения — значит узнать, какую скорость и положение будет иметь наш объект в любое интересующее нас время. А решить их можно. А значит, мы знаем все о поведении ракеты и поэтому можем понять, как будет оно изменяться при нашем вмешательстве. И какой вид вмешательства вообще выбрать.

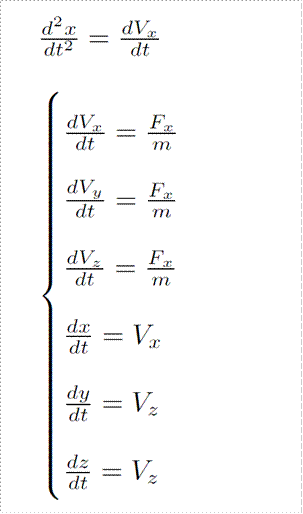
Однако, в текущем виде это еще не модель ракеты. Мы не описали правую часть — силы, на нее действующие. Давайте сделаем это.

1) Тяга двигателя

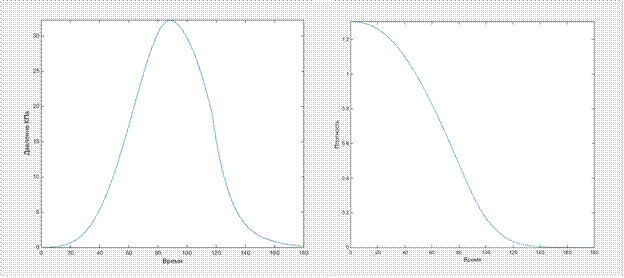
Одна из немногих добрых сил, толкающих нашу ракету к победе. Номинально она направлена по продольной оси ракеты, однако, в процессе полета отклоняется от нее, чтобы создать нужные моменты для поворота. Математически, в простейшем случае задается как произведение секундного расхода топлива на скорость истечения продуктов горения. Однако, это верно только если мы рассматриваем движение в безвоздушном пространстве, при наличии атмосферы тяга уже есть функция плотности воздуха, и определяется незамысловатым образом: чем ниже плотность, тем выше тяга, но, разумеется, изменение происходит в пределах от минимально возможной до максимальной. Эти минимаксы называются удельными импульсами у поверхности и в вакууме, этих двух цифр нам, в принципе, достаточно.

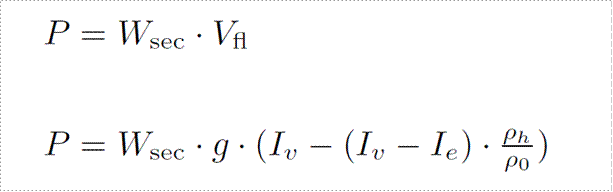
И добавили еще одно, седьмое — производную (скорость изменения) массы, чтобы учесть, что двигатель кушает топливо и ракета становится легче.

2) Аэродинамические силы

Чтобы рассмотреть их, введем несколько терминов:
Скорость ракеты не всегда совпадает с направлением продольной оси, поэтому эти направления надо смотреть раздельно. Пространственный угол атаки — это угол между продольной осью ракеты и вектором скорости. Этот угол можно разложить на две составляющие:
Угол атаки — угол между продольной осью и вектором горизонтальной скорости
Угол скольжения — угол между продольной осью и вектором боковой скорости

Получается, что при наличии (при их ненулевых значениях) этих углов ракета как бы «долбится» о воздух, а не «пронзает» его.
Основной закон аэродинамического сопротивления, используемый для описания движения ракет, выглядит так: аэродинамическое сопротивление есть половина текущей плотности воздуха на квадрат скорости на характерную площадь на аэродинамический коэффициент. Ее тоже раскладывают: лобовое сопротивление, боковая сила, подъемная сила. В основном всю аэродинамику сводят лишь к площади миделя (наибольшего поперечного сечения), но встречаются варианты с применением боковых площадей.

Аэродинамический коэффициент C — основная головная боль аэродинамиков. Именно от него зависит точность и корректность результата.

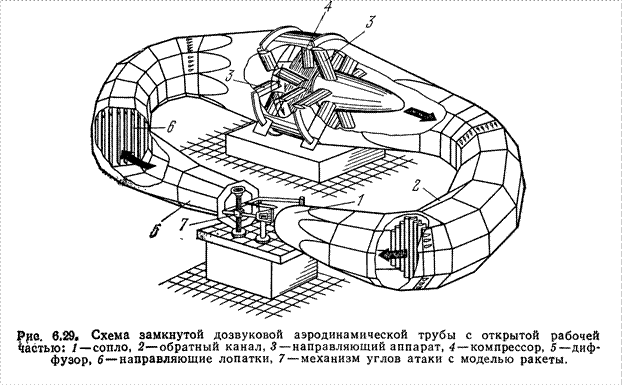
Его можно задавать константой, можно вычислять по специальным типовым таблицам, разбив корпус ракеты на примитивы; применять компьютерное моделирование; продувать в аэродинамических трубах. По факту наиболее годный и правильный результат дает совмещение двух последних методов, причем с развитием вычислительных мощностей наблюдается увеличение роли моделирования и сокращения экспериментальных работ. Однако о полном отказе речь пока не идет. После натурных испытаний в аэродинамическую модель вносятся последние штрихи.

Например, на небезызвестном buran.ru можно найти данные по поводу аэродинамики орбитального корабля. Понятно, что аэродинамика ракеты отличается немного меньшей сложностью, но цифры приведу:

«Создано 85 различных по сложности и масштабам аэродинамических моделей, 122 комплекта тензовесов к ним, 12 уникальных автоматизированных стендов для испытания моделей в трубах, специальные комплексы автоматизации измерений и их обработки. Общий объем продувок составил 36630 пусков в 25 трубах. Полный комплект аэродинамических характеристик корабля был оформлен отдельной книгой и претерпел три этапа уточнений.».

Запишем и эти силы в уравнения, учитывая их проекции.

3) Сила тяжести

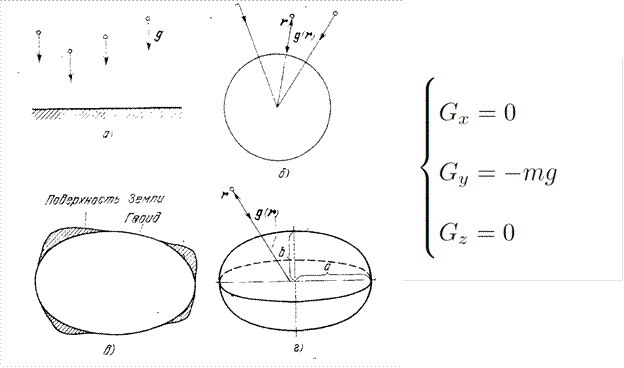
Представление силы тяжести в математической модели также варьируется от необходимой точности расчетных работ. Самый простой случай — плоскопараллельное гравитационное поле, где ускорение свободного падения постоянно на одной высоте и линейно с ней убывает. Небольшим усложнением является рассмотрение центрального гравитационного поля. Для повышенной точности используются представления Земли как эллипсоида. Еще одним шагом к уточнению модели будет учет наиболее характерных изменений толщины коры на участке, где проходит выведение ракеты. Однако, такие уточнения, мне думается, будут иметь смысл только для длительных прогнозов орбит спутников.

В статьях, посвященных управленческим задачам значения ускорения свободного падения часто заменяются просто прогнозируемым значением в конечной точке выведения.

Запишем ускорение свободного падения только по оси Y.

Добавим еще программу изменения угла тангажа.

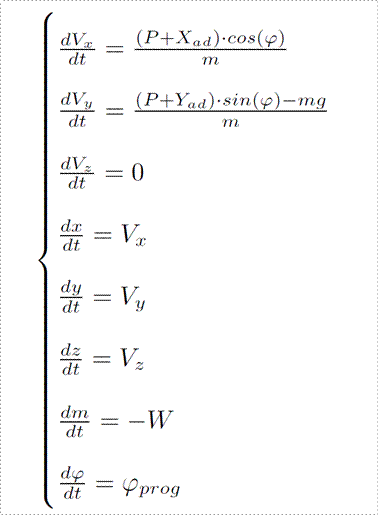
В итоге мы получили рабочую версию уравнений движения ракеты (вернее, ее центра масс). В каких-то случаях она будет слишком сложной, в каких-то — недостаточно точной. Например, баллистики работают с уравнениями большей точности, т.к. они не в целом не ограниченны по времени для расчетов. Математикам-управленцам обычно приходится прибегать к их измененному виду для возможности аналитического анализа и возможности полученные алгоритмы управления использовать в бортовом комплексе в режиме реального времени, который, конечно, не допустит хотя бы секундной задержки на «подумать».