
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 2. Практическое применение регрессионного анализа в эконометрике
Задача 1
По территории региона приводятся данные за 2007 (табл. 2.1).
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Решение: для расчета параметров уравнения линейной регрессии строим расчетную таблицу (табл. 2.2)
| х | у | Ху | х2 | у2 | |
| 1 | 78 | 133 | 10374 | 6084 | 17689 |
| 2 | 82 | 148 | 12136 | 6724 | 21904 |
| 3 | 87 | 134 | 11658 | 7569 | 17956 |
| 4 | 79 | 154 | 12166 | 6241 | 23716 |
| 5 | 89 | 162 | 14418 | 7921 | 26244 |
| 6 | 106 | 195 | 20670 | 11236 | 38025 |
| 7 | 67 | 139 | 9313 | 4489 | 19321 |
| 8 | 88 | 158 | 13904 | 7744 | 24964 |
| 9 | 73 | 152 | 11096 | 5329 | 23104 |
| 10 | 87 | 162 | 14094 | 7569 | 26244 |
| 11 | 76 | 159 | 12084 | 5776 | 25281 |
| 12 | 115 | 173 | 19895 | 13225 | 29929 |
| Итого | 1027 | 1869 | 161808 | 89907 | 294377 |
| Среднее значение | 85,6 | 155,8 | 13484,0 | 7492,3 | 24531,4 |
| σ | 12,95 | 16,53 | - | - | - |
| σ2 | 167,7 | 273,4 | - | - | - |
b=xy-y*x/∑x2-(x)2=(13484-85,6*155,8)/(7492,3-85,62)=151,8/164,94=0,92
a=y-b*x=155,8-0,92*85,6=77,0
Получено уравнение регрессии: у=77,0+0,92*х.
С увеличением среднедушевого прожиточного минимума на 1 рубль среднедневная заработная плата возрастает в среднем на 0,92 рубля.
Задача 2
По семи территориям Уральского района за 2008 г. Известны значения двух признаков (табл. 2.3).
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская республика | 68,8 | 45,1 |
| Свердловская область | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская область | 56,7 | 61,8 |
| Пермская область | 55,0 | 58,8 |
| Курганская область | 54,3 | 47,2 |
| Оренбургская область | 49,3 | 55,2 |
Определить:
1.
Для характеристики зависимости у от х рассчитать параметры следующих функций:
А. линейной, ценить ее через F-критерий Фишера.
Б. степенной
Решение:
1.А. Для расчета параметров а и b линейной регрессии ŷx=а+b*x решаем систему нормальных уравнений относительно а и b:
n*a+b∑x=∑y,
a∑x+b∑x2=∑y*x.
По исходным данным рассчитываем: ∑x, ∑y, ∑x2, ∑y*x, ∑y2. (Табл. 2.4)
b= yx-y*x/ σx2=(3166,05-57,89*54,9)/(5,86)2=-0,35;
a=y-b*x=57,89+0,35*54,9=76,88.
Уравнение регрессии: ŷ=76,8-0,35*х
| 1 | 68,8 | 45,1 | 3102,88 | 2034,01 | 4733,44 |
| 2 | 61,2 | 59,0 | 3610,80 | 3481,00 | 3745,44 |
| 3 | 59,9 | 57,2 | 3426,28 | 3271,84 | 3588,01 |
| 4 | 56,7 | 61,8 | 3504,06 | 3819,24 | 3214,89 |
| 5 | 55,0 | 58,8 | 3234,00 | 3457,44 | 3025,00 |
| 6 | 54,3 | 47,2 | 2562,96 | 2227,84 | 2948,49 |
| 7 | 49,3 | 55,2 | 2721,36 | 3047,04 | 2430,49 |
| Итого | 405,2 | 384,3 | 22162,34 | 21338,41 | 23685,76 |
| Среднее значение | 57,89 | 54,90 | 3166,05 | 3048,34 | 3383,68 |
| σ | 5,74 | 5,89 | - | - | - |
| σ2 | 32,92 | 34,34 | - | - | - |
С увеличением среднедневной заработной платы на 1 рубль доля расходов на покупку продовольственных товаров снижается в среднем на 0,35%-ных пункта.
Рассчитаем линейный коэффициент парной корреляции:
rxy=b*σx /σy=-0,35*5,86/5,74=-0,357.
Связь умеренная, обратная.
Определим коэффициент детерминации:
r2xy=(-0,35)2=0,127.
Вариация результата на 12,7% объясняется вариацией фактора х.
Рассчитаем F-критерий:
Fфакт= r2xy*(n-2)/(1- r2xy)=0,127*5/0,873=0,7.
Поскольку 1≤F≤∞, следует рассмотреть F-1.
Полученное значение указывает на необходимость принять гипотезу Н0 о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
1.Б. построению степенной модели ŷx=а*xb предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
lg y=lg a + b*lg x;
Y = C + b*X, где
Y = lg y, X = lg x, С = lg a.
Для расчетов построим таблицу (табл. 2.5)
| х | у | Х | У | Х*У | Х2 | У2 | |
| 1 | 68,8 | 45,1 | 1,6542 | 1,8376 | 3,0398 | 2,7364 | 3,3768 |
| 2 | 61,2 | 59,0 | 1,7709 | 1,7868 | 3,1642 | 3,1361 | 3,1927 |
| 3 | 59,9 | 57,2 | 1,7574 | 1,7774 | 3,1236 | 3,0885 | 3,1592 |
| 4 | 56,7 | 61,8 | 1,7910 | 1,7536 | 3,1407 | 3,2077 | 3,0751 |
| 5 | 55,0 | 58,8 | 1,7694 | 1,7404 | 3,0795 | 3,1308 | 3,0290 |
| 6 | 54,3 | 47,2 | 1,6739 | 1,7348 | 2,9039 | 2,8019 | 3,0095 |
| 7 | 49,3 | 55,2 | 1,7419 | 1,6928 | 2,9487 | 3,0342 | 2,8656 |
| Итого | 405,2 | 384,3 | 12,1587 | 12,3234 | 21,4003 | 21,1355 | 21,7078 |
| Среднее значение | 57,89 | 54,90 | 1,7370 | 1,7605 | 3,0572 | 3,0194 | 3,1011 |
| σ2 | 32,92 | 34,34 | 0,0023 | 0,0018 | - | - | - |
Рассчитаем С и b:
b=(YX-Y*X)/ σ2X=3,0572-1,7605*1,7370/0,04842=-0,298;
C=Y-b*X=1,7605+0,298*1,7370=2,278.
Получим линейное уравнение: Ŷ=2,278-0,298*Х.
Выполнив его потенцирование, получим:
ŷ=102,278*х-0,298=189,7* х-0,298.
Задача 3
Руководство предприятия заметило, что годовой товарооборот зависит не только от торговой площади магазина (см. пример 2.1), но и от среднего числа посетителей. Соответствующая информация представлена в табл. 2.3.
Таблица 2.3
| Номер магазина | Среднее число посетителей в день, тыс. чел. |
| 8,25 | |
| 10,24 | |
| 9,31 | |
| 11,01 | |
| 8,54 | |
| 7,51 | |
| 12,36 | |
| 10,81 | |
| 9,89 | |
| 13,72 | |
| 12,27 | |
| 13,92 |
Решение. Обозначим 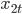 — среднее число посетителей
— среднее число посетителей  -го магазина в день, тыс. чел.
-го магазина в день, тыс. чел.
Для определения формы функциональной зависимости между переменными 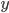 и
и 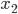 построим диаграмму рассеяния (рис. 2.2).
построим диаграмму рассеяния (рис. 2.2).
На основании диаграммы рассеяния можно сделать вывод о позитивной зависимости годового товарооборота от среднего числа посетителей в день (т.е. у будет расти с ростом 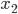 ). Форма функциональной зависимости — линейная.
). Форма функциональной зависимости — линейная.
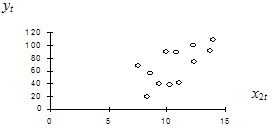
Рис. 2.2. Диаграмма рассеяния для примера 2.2
Таблица 2.4
| t | x2t | x2t 2 | yt x2t | x1t x2t |
| 8,25 | 68,0625 | 163,02 | 1,98 | |
| 10,24 | 104,8575 | 390,0416 | 3,1744 | |
| 9,31 | 86,6761 | 381,2445 | 5,1205 | |
| 11,01 | 121,2201 | 452,2908 | 5,2848 | |
| 8,54 | 72,9316 | 480,7166 | 6,6612 | |
| 7,51 | 56,4001 | 514,5101 | 7,3598 | |
| 12,36 | 152,7696 | 927,1236 | 11,6184 | |
| 10,81 | 116,8561 | 962,6305 | 13,0801 | |
| 9,89 | 97,8121 | 901,2757 | 12,7581 | |
| 13,72 | 188,2384 | 1252,0872 | 15,3664 | |
| 12,27 | 150,5529 | 1225,0368 | 15,8283 | |
| 13,92 | 193,7664 | 1511,016 | 20,7408 | |
| S | 127,83 | 1410,44 | 9160,9934 | 118,9728 |
| Cреднее | 10,65 |
В целом необходимо определить параметры двухфакторной эконометрической модели
уt= a0+ a1х1t+ a2х2t+ εt
Информация, требующаяся для дальнейших расчетов, представлена в табл. 2.4.
Оценим параметры линейной двухфакторной эконометрической модели с помощью метода наименьших квадратов.

Таким образом,
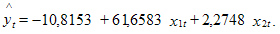
Оценка коэффициента 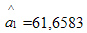 =61,6583 показывает, что при прочих равных условиях с увеличением торговой площади на 1 тыс. м2 годовой товарооборот увеличится в среднем на 61,6583 млн руб.
=61,6583 показывает, что при прочих равных условиях с увеличением торговой площади на 1 тыс. м2 годовой товарооборот увеличится в среднем на 61,6583 млн руб.
Оценка коэффициента 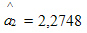 = 2,2748 показывает, что при прочих равных условиях с увеличением среднего числа посетителей на 1 тыс. чел. в день годовой товарооборот увеличится в среднем на 2,2748 млн руб.
= 2,2748 показывает, что при прочих равных условиях с увеличением среднего числа посетителей на 1 тыс. чел. в день годовой товарооборот увеличится в среднем на 2,2748 млн руб.
Выводы:
В практических исследованиях возникает необходимость аппроксимировать (описать приблизительно) зависимость между переменными величинами у и х. Ее можно выразить аналитически с помощью формул и уравнений и графически в виде геометрического места точек в системе прямоугольных координат. Для выражения регрессии служат эмпирические и теоретические ряды, их графики — линии регрессии, а также корреляционные уравнения (уравнения регрессии) и коэффициент линейной регрессии.
Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение средней величины  признака у при изменении значений xi признака х, и, наоборот, показывают изменение средней величины
признака у при изменении значений xi признака х, и, наоборот, показывают изменение средней величины  признака х по измененным значениям yi признака у.
признака х по измененным значениям yi признака у.
Форма связи между показателями может быть разнообразной. И поэтому задача состоит в том, чтобы любую форму корреляционной связи выразить уравнением определенной функции (линейной, параболической и т.д.), что позволяет получать нужную информацию о корреляции между переменными величинами у и х, предвидеть возможные изменения признака у на основе известных изменений х, связанного с у корреляционно.
Заключение:
В настоящее время регрессионный анализ используется как в естественнонаучных исследованиях, так и в обществоведении.
В практических исследованиях возникает необходимость аппроксимировать (описать приблизительно) зависимость между переменными величинами у и х. Ее можно выразить аналитически с помощью формул и уравнений и графически в виде геометрического места точек в системе прямоугольных координат. Для выражения регрессии служат эмпирические и теоретические ряды, их графики — линии регрессии, а также корреляционные уравнения (уравнения регрессии) и коэффициент линейной регрессии.
Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение средней величины  признака у при изменении значений xi признака х, и, наоборот, показывают изменение средней величины
признака у при изменении значений xi признака х, и, наоборот, показывают изменение средней величины  признака х по измененным значениям yi признака у.
признака х по измененным значениям yi признака у.
Форма связи между показателями может быть разнообразной. И поэтому задача состоит в том, чтобы любую форму корреляционной связи выразить уравнением определенной функции (линейной, параболической и т.д.), что позволяет получать нужную информацию о корреляции между переменными величинами у и х, предвидеть возможные изменения признака у на основе известных изменений х, связанного с у корреляционно.
Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна.
Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.
Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.
Решение задач основывается на анализе соответствующих параметров (статистических данных) в которых всегда неизбежно присутствуют отклонения, вызванные случайными ошибками. Поэтому существуют специальные методы оценки как уравнения регрессии в целом, так и отдельных ее параметров.
Построение линейной регрессии сводится к оценке ее параметров – a и b. Оценки параметров линейной регрессии могут быть найдены разными методами. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов
В прогнозных расчетах по уравнению регрессии путем подстановки в него соответствующего значения х определяется предсказываемое значение. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки ŷx, то есть mŷx, и соответственно интервальной оценкой прогнозного значения (у*).
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера.
Date: 2015-07-25; view: 577; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |