
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Получение логических следствий из данных формул и посылок для данных логических следствий
Логические следствия находят следующим образом:
1) все посылки соединяются конъюнкцией и находятся СКНФ полученной формулы.
2) при выборе любых элементарных дизъюнкций и конъюнкций любых нескольких элементарных дизъюнкций, взятых по два, три и т.д.
получаются все возможные заключения из данных посылок.
Задача 1. Даны посылки: A и A 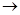 B
B
Решение:
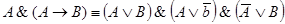
Логические следствия:
1.  ;
;
2. 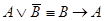 ;
;
3. 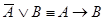 ;
;
4. 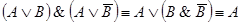 ;
;
5.  ;
;
6. 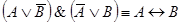 ;
;
7. 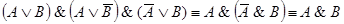 .
.
Задача 2. Даны посылки: 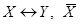
Решение:
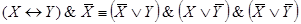
Логические следствия:
1. 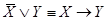 ;
;
2. 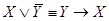 ;
;
3. 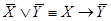 ;
;
4. 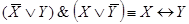 ;
;
5. 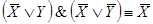 ;
;
6. 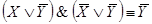 ;
;
7. 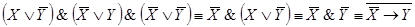 .
.
Задача 3. Даны посылки: 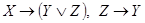
Решение:
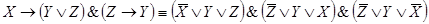
Логические следствия:
1. 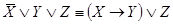 ;
; 
2. 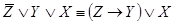 ;
;
3. 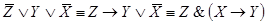 ;
;
4. 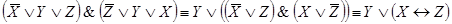 ;
;
5. 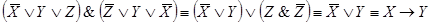 ;
;
6. 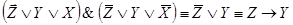 ;
;
7. 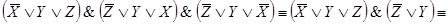
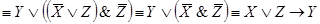 ;
;
Задача 4. Найти формулу F(X, Y), зависящую только от переменных X и Y и являющуюся логическим следствием указанных формул (посылок):
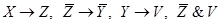
Решение:
Составим таблицу истинности для формул, являющихся посылками:
| X | Y | Z | V | 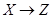
| 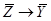
| 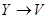
| 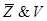
| |
| * |
В правом столбце звездочками отметим те строки, в которых все четыре посылки принимают значение 1. Этому требованию удовлетворяет лишь 15-я строка, в которой λ (X) = 0 и λ (Y) = 0. Следовательно, надо найти такую формулу F (X, Y), для которой F (0, 0) = 1, то такая формула будет логическим следствием четырех данных посылок. Ищем такую формулу, используя СДНФ и считаем, что на всех других наборах значений переменных искомая формула обращается в 0:
F (0, 1) = F (1, 0) = F (1, 1) = 0.
Получаем F (X, Y) 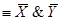 .
.
Задача 5. Найти формулу F(X, Y), зависящую только от переменных X и Y и являющуюся логическим следствием указанных формул (посылок):
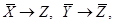
Решение:
Составим таблицу истинности для формул, являющихся посылками:

| X | Y | Z | 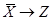
| 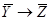
| |
| * * * * |
Найдем такую формулу F (X, Y), для которой F (1, 1) = F (0, 1) = F (1, 0) = 1, которая будет логическим следствием двух данных посылок.
F (0, 0) = 0.
Получаем F (X, Y) 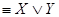 .
.
Задача 6. Найти формулу F(X, Y), зависящую только от переменных X и Y и являющуюся логическим следствием указанных формул (посылок):
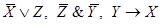
Решение:
Составим таблицу истинности для формул, являющихся посылками: 
| X | Y | Z | 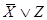
| 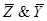
| 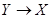
| |
| * * |
Найдем такую формулу F (X, Y), для которой F (0, 0) = 1, которая будет логическим следствием трех данных посылок.
F (1, 0) = F (0, 1) = F (1, 1) = 0.
Получаем F (X, Y) 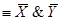 .
.
Чтобы определить логическим следствием каких посылок является формула А (X1,X2,…,Xn), необходимо:
1) привести ее к СКНФ.
2) составить конъюнкции формулы А с недостающими в ее СКНФ элементарными дизъюнкциями, взятыми по одной, две, три и т.д. (всевозможные варианты). Полученные формулы и будут посылками, из которых следует данная формула А.
Найти все не тождественно ложные формулы алгебры высказываний, для которых следующая формула является логическим следствием:
Задача 1. 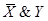
Решение:
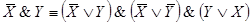
Недостающие дизъюнкции: 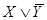
Посылка:


Данная формула может логически следовать либо из самой себя, либо из тождественно ложной формулы.
Задача 2. 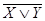
Решение:
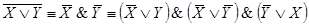
Недостающие дизъюнкции: 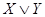
Посылка:
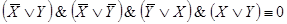
Данная формула может логически следовать либо из самой себя, либо из тождественно ложной формулы.
Задача 3. 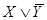
Решение:
Недостающие дизъюнкции: 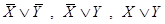
Посылки:
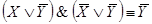 ;
;
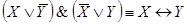 ;
;
 ;
;
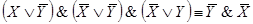 ;
;
 ;
;
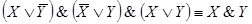 ;
;
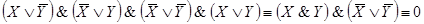 .
.
Данная формула может логически следовать либо из самой себя, либо из тождественно ложной формулы.
Задача 4. Найти недостающую посылку (формулу) F, зависящую лишь от указанных высказываний, чтобы была верна следующая выводимость:
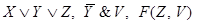 ╞
╞ 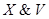
Решение:
Составим таблицу истинности для формул, являющихся посылками и заключением:
| X | Y | Z | V | 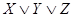
| 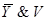
| 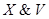
| |
| * |
В правом столбце звездочками отметим те строки, в которых обе данные посылки принимают значение 1, а следствие принимает значение 0. Этому требованию удовлетворяет лишь 12-я строка, в которой λ (Z) = 1 и λ (V) = 1. Ясно, что при этих значениях Z и V искомая посылка F (Z, V) должна принимать значение 0, так как в противном случае формула 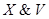 не будет логическим следствием формул
не будет логическим следствием формул 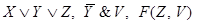 . Будем считать, что на других наборах значений высказываний Z и V формула F (Z, V) принимает значение 1. Итак, для искомой посылки F (Z, V) получаем следующую таблицу истинности:
. Будем считать, что на других наборах значений высказываний Z и V формула F (Z, V) принимает значение 1. Итак, для искомой посылки F (Z, V) получаем следующую таблицу истинности:
| Z | V | F(Z, V) |
Находим СКНФ для искомой формулы. Получаем F (Z, V)  .
.
Задача 5. Найти недостающую посылку (формулу) F, зависящую лишь от указанных высказываний, чтобы была верна следующая выводимость:
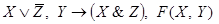 ╞
╞ 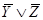
Решение:
Составим таблицу истинности для формул, являющихся посылками и заключением:
| X | Y | Z | 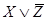
| 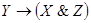
| 
| |
| * |
В правом столбце звездочками отметим те строки, в которых обе данные посылки принимают значение 1, а следствие принимает значение 0. Этому требованию удовлетворяет лишь 1-я строка, в которой λ (X) = 1 и λ (Y) = 1. Будем считать, что на других наборах значений высказываний X и Y формула F (X, Y) принимает значение 1. Итак, для искомой посылки F (X, Y) получаем следующую таблицу истинности:
| X | Y | F(X, Y) |
Находим СКНФ для искомой формулы. Получаем F (X, Y) 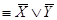 .
.
Задача 5. Найти недостающую посылку (формулу) F, зависящую лишь от указанных высказываний, чтобы была верна следующая выводимость:
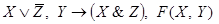 ╞
╞ 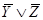
Решение:
Составим таблицу истинности для формул, являющихся посылками и заключением:
| X | Y | Z | 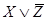
| 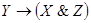
| 
| |
| * |
В правом столбце звездочками отметим те строки, в которых обе данные посылки принимают значение 1, а следствие принимает значение 0. Этому требованию удовлетворяет лишь 1-я строка, в которой λ (X) = 1 и λ (Y) = 1. Будем считать, что на других наборах значений высказываний X и Y формула F (X, Y) принимает значение 1. Итак, для искомой посылки F (X, Y) получаем следующую таблицу истинности:
| X | Y | F (X, Y) |
Находим СКНФ для искомой формулы. Получаем F (X, Y) 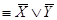 .
.
Задача 5. Найти недостающую посылку (формулу) F, зависящую лишь от указанных высказываний, чтобы была верна следующая выводимость:
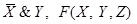 ╞
╞ 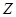
Решение:
Составим таблицу истинности для формул, являющихся посылками и заключением:
| X | Y | Z | 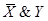
| Z | |
| * |
В правом столбце отметим строку, в которой данная посылка принимает значение 1, а следствие принимает значение 0. Этому требованию удовлетворяет лишь 6-я строка, в которой λ (X) = 0, λ (Y) = 1 и λ (Z) = 0. Будем считать, что на других наборах значений высказываний X, Y, Z формула F (X, Y, Z) принимает значение 1. Итак, для искомой посылки F(X, Y, Z) получаем следующую таблицу истинности:
| X | Y | Z | F (X,Y, Z) |
Находим СКНФ для искомой формулы. Получаем
F (X, Y, Z) 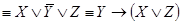 .
.
Date: 2015-07-25; view: 11677; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |