
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Способы вычисления эластичности спроса
Рассчитывая коэффициент эластичности, следует решить одну проблему: какие показатели цены и количества продукции использовать в вычислениях?
Существуют 2 способа вычисления коэффициента эластичности. Первый позволяет определить точечную эластичность (эластичность в точке). Она характеризует относительное изменение спроса при бесконечно малом изменении цены. Это в реальности встречается либо на монополизированном рынке, либо в определенной точке сбыта товара в краткосрочном периоде.
Точечная эластичность - это предельная концепция в том смысле, что она определяет эластичность в специфической точке на кривой спроса. Мы можем определить точечную эластичность по формуле [3, с. 114]:
| ∆Q P Ed = —— × ——, ∆ P Q | (2.1) |
где Рx, – цена продукции;
Qx - количество продукции.
Если кривая спроса задается линейной функцией Q = a – bP, то ее наклон совпадает с наклоном касательной во всех точках на кривой спроса и равен ∆Q / ∆P = - b. Точечная эластичность линейной функции может выражаться тогда так [8, с. 254]:
| P Ed = - b ——, Q | (2.2) |
где b – наклон кривой спроса.
Точечная эластичность может быть определена, если провести касательную к кривой спроса. Наклон кривой спроса в любой своей точке, как известно, определяется значением тангенса угла касательной с осью Х (рис. 2.1).
 |
Рис. 2.1. Точечная эластичность [8, с. 253]
Значение точечной эластичности обратно пропорционально тангенсу угла наклона.
Рассмотрим функцию спроса Qx= 30 - 2Рx, где Qx представляет требуемое количество, а Рx— цену продукта X. Какова ценовая эластичность в точке на кривой спроса, где Рx= 6?
По формуле (2.2) мы получаем:
| 6 6 Ed = (- 2) × ————— = (- 2) × —— = - 0,67. 30 – (2 × 6) 18 |
Это может означать, что если цена составляет 6 долл., то изменение на 1% в цене может вызвать изменение на 0,67% в требуемом количестве. Знак «минус» означает, что переменные движутся в противоположном направлении.
Если кривая спроса линейная, то ее наклон постоянен. Отношение P/Q, однако, разное в каждой точке вдоль линии. Следовательно, эластичность различна в каждой точке на линии, независимо от того, является ли кривая линейной или не является.
Если имеется множество независимых переменных в функции спроса, то точка эластичности каждой переменной X, может быть найдена с помощью частных производных. Если функция спроса линейная, то частные производные оказываются коэффициентами соответствующих переменных.
Во избежание неопределенности в расчетах обычно используют средние для анализируемого периода значения цены и количества продукции. Такой способ расчета позволяет вычислить коэффициент дуговой эластичности.
Как уже говорилось ранее, формула точечной эластичности (2.1) отражает предельную концепцию и она действительна лишь для небольших передвижений от точки к точке вдоль кривой спроса. Более того, из формулы (2.1) следует, что необходимо знать точное изменение в Qx, вызванное очень малым изменением в Px, т.е. требуется, чтобы функция спроса была известна. Однако имеется много случаев, когда нам нужно измерить эластичность, а функция спроса неизвестна. Бывает, что нас интересует более крупный сегмент кривой спроса. Для этого нам необходима формула дуговой эластичности, которая вычисляла бы среднюю эластичность между двумя точками на кривой спроса.
Чтобы объяснить сущность формулы дуговой эластичности, предположим, что цена папуа (тропического фрукта) в супермаркете «Safeway» в Гонолулу снизилась с 0,50 долл. за фунт до 0,38 долл. за фунт, вследствие чего средние продажи папуа увеличились с 300 до 450 фунтов в день [6, с. 372].
Эти данные определяют две точки вдоль кривой спроса. Какова средняя эластичность между этими двумя точками? Если мы возьмем верхнюю точку (50; 300) за нашу базовую точку, то получим:
| процентное изменение Qx (450 – 300) / 300 Эластичность цены = ——————————— = ———————— = процентное изменение Px (38 – 50) / 50 |
| 450 - 300 50 150 50 = ———— × ———— = ——— × ——— = - 2,08. 300 38 - 50 300 - 12 |
Если мы используем нижнюю точку (38; 450) в качестве нашей базовой точки и будем перемещаться по кривой, то:
| (300 – 450) / 450 300 - 450 38 Ценовая эластичность = ———————— = ————— × ——— = (50 – 38) / 38 450 50 - 38 |
| - 150 38 = ——— × —— = - 1,06. 450 12 |
Теперь мы видим, что ценовая эластичность папуа совершенно различна в верхнем и нижнем концах этого сегмента кривой спроса.
Что делать? Решение заключается в том, чтобы найти среднюю эластичность для данного приращения меняющегося спроса. Для того чтобы сделать это, нам необходимо изменить базу для вычисления эластичности на среднее между двумя базами (P1, Q1,) и (Р2, Q2) на концах дуги. Средняя цена составляет (Р2 + Р1)/2, а среднее требуемое количество равно (Q2 + Q1)/2. Эти средние координаты определяют точки на полпути между ними вдоль прямой линии. Затем мы модифицируем базисное определение эластичности, чтобы получить формулу дуговой эластичности с использованием средних координат Р и Q. Изменения в Р и Q — это изменения между конечными точками, т.е. ∆Р = Р2 — Р1 и ∆Q = Q2 — Q1. Мы обозначаем дуговую эластичность как ed, а не Ed, для того, чтобы отличить дуговую эластичность от точечной эластичности.
Таким образом, формула расчета дуговой эластичности имеет вид [6, с. 371]:
| ∆Q (P0 + P1) / 2 ∆Q P ed = —— × —————— = —— × ——. ∆P (Q0 + Q1) / 2 ∆P Q | (2.3) |
Применив формулу дуговой эластичности (2.3) к нашему примеру, получим:
| (450 – 300) (38 + 50) 150 × 88 13 200 ed = ————— × —————— = ————— = ———— ≈ - 1,47. (38 – 50) (450 + 300) - 12 × 750 - 9 000 |
Это означает, что в среднем в пределах изменения цен от 50 до 38 центов за фунт при изменении цен на папуа на 1% требуемое количество будет меняться на 1,47%.
В том случае, когда функция спроса носит непрерывный характер, дуговая эластичность заменяется точечной, понимаемой как предел дуговой эластичности по мере того, как длина дуги стремится к нулю, то есть при бесконечно малом изменении цены.
В этом случае [6, с. 374]:
∆Q 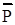 ∂Q P
ed = ∂Q P
ed = 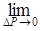 —— × —— = —— × ——.
∆P Q ∂P Q —— × —— = —— × ——.
∆P Q ∂P Q
| (2.4) |
Точечная эластичность — это предельная концепция, потому что она измеряет эластичность в конкретной точке кривой спроса Она может быть использована для анализа воздействий очень небольших изменений в цене. Более широкая концепция дуговой эластичности позволяет проводить измерения средней эластичности по более широкому диапазону изменений в цене. Дуговая эластичность, таким образом, более адекватный инструмент анализа эмпирических данных, касающихся цен и требуемых количеств.
Date: 2015-07-25; view: 671; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |