Проблема некорректности задачи идентификации

При решении уравнения Винера-Хопфа численными методами вместо гладкой кривой g(t) в ряде случаев можно получить кривую. Имеющую скачкообразный характер и даже отдельно не напоминающую импульсную переходную функцию исследуемого объекта (рисунок 15)

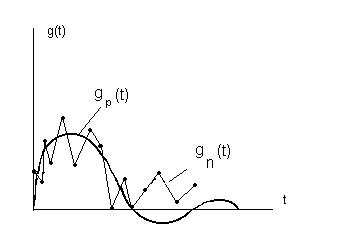
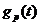-ИПФ реального объекта;

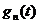-ИПФ, найденная при решении задачи идентификации.

Если попытаться увеличить количество точек, в которых рассчитывается g(t), то получим еще более неутешительную картину.

Эти факты объясняются некорректностью математической подстановки рассматриваемой задачи. Существует широкий класс так называемых обратных задач в физике и технике, которые являются некорректно поставленными [15].

Классическое определение корректности задачи дал французский математик Ж.Адамар. Задача считается корректно поставленной, если выполняются следующие три условия:

1. Решение задачи Ах=u существует, т.е. существует х, удовлетворяющий уравнению Ах=u при данных A, u.

2. Решение единственно, т.е. искомая функция единственна для конкретных A,u.

3. Решение устойчиво, т.е. при непрерывном изменении исходных данных решение изменяется непрерывно. Бесконечно малым вариациям исходных данных соответствуют бесконечно малые вариации решения.

Задача определения импульсной переходной функции из уравнения Винера-Хопфа некорректна из-за невыполнения третьего условия: малые ошибки в исходных данных – в 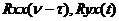приводят к ошибкам в решении. Степень неустойчивости в высшей мере зависит от гладкости ядра 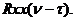Чем более гладкой является эта функция, тем выше получается коэффициент усиления ошибки. Гладкость функции зависти от коррелированности входного сигнала.

Покажем, что даже малые ошибки в 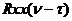могут приводить к значительным ошибкам в решении уравнения Винера-Хопфа. Итак, дано уравнение

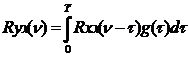(119)

т.к. входные и выходные сигналы объекта измерялись с ошибками, считаем, что решением уравнения является 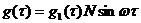, где 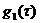-истинная импульсная переходная функция.

Тогда

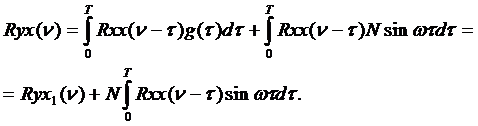(120)

Здесь R _yx1(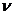)-истинная взаимнокорреляционная функция, а второй член уравнения – добавка за счет погрешностей измерения.

Оценим уклонение R _yx(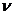) от R _yx1(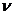) в пространстве L₂:

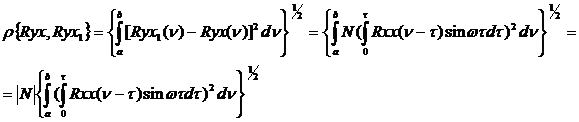(121)

Это уклонение для любого N при достаточно большом 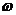можно сделать как угодно малым. Вспомним, что 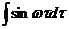есть 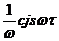, таким образом,

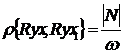. (122)

А теперь рассмотрим уклонение решения g (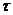) от истинного значения g ₁(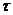). Расстояние определим по равномерной метрике

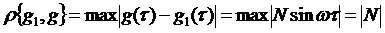(123)

Поскольку N может быть любым числом, то расстояния между истинным значением g ₁(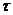) и решением уравнения g (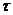) может быть сколько угодно большим. И это несмотря на малое отличие между R _yx1(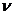) и R _yx().

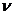Алгебраическая некорректность (неустойчивость) задачи идентификации проявляется в том, что определитель обращаемой матрицы близок к нулю. Если увеличивается размер той матрицы, то строки ее становятся более близки друг к другу. Кроме того увеличивается число операций при определении определителя, а следовательно, и погрешность его вычисления. При определении коэффициентов модели объекта управления в статике необходимо выполнять обращение матрицы X^TX. Определитель этой матрицы близок к нулю, если входные сигналы объекта управления коррелированны между собой. Таким образом, при решении задачи идентификации и в статике, и в динамике приходится сталкиваться с неустойчивостью решения.

Для решения некорректных задач разработаны специальные методы, называемые методами регуляризации. Регуляризация – преодоление некорректности. Эффект от регуляризации обусловлен тем, что при решении некорректной задачи используется дополнительная информация.

Одним из наиболее известных и широко распространенных является метод регуляризации А.Н.Тихонова [15]. Рассмотрим применение метода на примере дискретного уравнения Винера-Хопфа. Вспомним, что решение этого уравнения ищется из условия минимума функционала

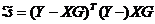. (124)

А в методе Тихонова решение G отыскивается среди множеств возможных решений, удовлетворяющих требованию минимума стабилизирующего функционала

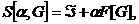(125)

где 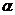- параметр регуляции,

F[G] - регулирующий функционал.

Рассмотрим в качестве регулирующего функционала функционал вида 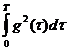, или в дискретном виде G^T G.

Запишем функционал S:

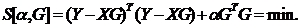(126)

Из условия 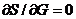определим G:

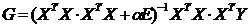(127)

Если известна среднеквадратичная ошибка измерения сигналов на входе объекта 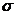, то

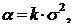(128)

где k - коэффициент пропорциональности [20]

Параметр 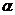можно подобрать так же экспериментальным путем, проделав несколько результатов вычислений G.

Другой метод регуляризации заключается в замене исходного уравнения идентификации

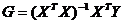(129)

близким ему уравнением, для которого задача нахождения решения устойчива к малым изменениям исходных данных

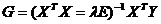(130)

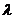- параметр регуляризации.

Идея этого метода принадлежит академику Лаврентьеву. Отметим, что к такому же алгоритму приводят и некоторые другие методы регуляризации. Добавление к главной диагонали обращаемой матрицы элемента 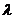приводит к тому, что определитель матрицы становится отличным от нуля и решение получается гладкое.

Метод регуляризации Л.П.Грабарь основан на разложении сигналов x(t) и y(t) по системе ортогональных полиномов. Несколько первых коэффициентов разложения несут в себе основную часть информации об изменении функций времени x(t) и y(t). Матрица, которую необходимо обращать при решении задачи идентификации, так же имеет небольшую размерность и определитель ее не равен нулю.

Разработанные советскими математиками методы регуляризации успешно позволяют решать некорректно поставленные задачи, в том числе задачу идентификации.