Измерение степени тесноты корреляционной связи

Показатели степени тесноты связи дают возможность охарактеризовать зависимость вариации результативного признака от вариации признака-фактора. В известной мере они дополняют и развивают уже отмеченные приёмы обнаружения связи.

Зная показатели тесноты корреляционной связи, можно решать следующие группы вопросов:

1. ответить на вопрос о необходимости изучения данной связи между признаками и целесообразности её практического применения;

2. сопоставляя показатели тесноты связи для различных ситуаций, можно судить о степени различий в её проявлении для конкретных условий;

3. и, наконец, сопоставляя показатели тесноты связи результативного признака с различными факторами, которые в данных конкретных условиях являются решающими и, главным образом, воздействуют на формирование величины результативного признака.

К простейшим показателям степени тесноты связи относят коэффициент корреляции знаков, который был предложен немецким учёным Г. Фехнером (1801 – 1887). Этот показатель основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Для его расчёта вычисляют средние значения результативного и факторного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязанных пар признаков.

Если ввести обозначения: na – число совпадений знаков отклонений индивидуальных величин от средней, nb – число несовпадений знаков отклонений, то коэффициент Фехнера можно записать таким образом:

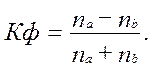(1.18)

Коэффициент Фехнера может принимать различные значения в пределах от –1 до +1. Если знаки всех отклонений совпадут, то nb = 0 и тогда показатель будет равен 1, что свидетельствует о возможном наличии прямой связи. Если же знаки всех отклонений будут разными, тогда na = 0b и коэффициент Фехнера будет равен –1, что даёт основание предположить наличие обратной связи.

Более совершенным показателем степени тесноты связи является линейный показатель корреляции (r)*.

При расчёте этого показателя учитываются не только знаки отклонений индивидуальных значений признака от средней, но и сама величина таких отклонений, т.е. соответственно для факторного и результативного признаков величины.

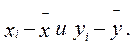(1.19)

Однако непосредственно сопоставлять между собой полученные абсолютные величины нельзя, так как сами признаки могут быть выражены в разных единицах (как это имеет место в представленном примере), а при наличии одних и тех же единиц измерения средние могут быть различны по величине. В этой связи сравнению могут подлежать отклонения, выраженные в относительных величинах, т.е. в долях среднего квадратического отклонения (их называют нормированными отклонениями). Так, для факторного признака будем иметь совокупность величин:

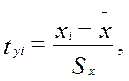(1.20)

а для результативного

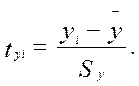(1.21)

Выполнив несложные преобразования, можно получить следующую формулу для расчёта линейного коэффициента корреляции:

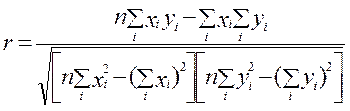. (1.22)

При пользовании этой формулой отпадает необходимость вычислять отклонения индивидуальных значений признаков от средней величины, что исключает ошибку в расчётах при округлении средних величин.

Линейный коэффициент корреляции может принимать любые значения в пределах от –1 до +1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи: прямой зависимости соответствует знак плюс, а обратной зависимости – знак минус.

Если с увеличением факторного признака x результативный признак y имеет тенденцию к увеличению, то величина коэффициента корреляции будет находиться между 0 и 1. Если же с увеличением значений x результативный признак y имеет тенденцию к снижению - коэффициент корреляции может принимать значения в интервале от 0 до –1.

Вторым этапом изучения статистической связи вслед за определением степени тесноты связи с помощью коэффициента корреляции идет этап установления формы связи или вида функции φ (х), объясняющей основную закономерность влияния факторного признака х на результативный признак у.

Под формой статистической связи понимают ту тенденцию, которая проявляется в изменении изучаемого результативного признака в связи с изменением факторного признака. Форму связи можно попытаться установить, построив в прямоугольной системе координат все множество пар значений признаков (х_i, у_i), 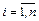. По оси абсцисс откладываются значения факторного признака х, по оси ординат – значения признака у. Такое графическое построение называется полем корреляции или диаграммой рассеяния, пример построения представлен на рис. 3.3. По характеру расположения точек на координатной плоскости можно судить о характере статистической связи. Если наблюдается тенденция равномерного возрастания или убывания значений признака, то связь называется прямолинейной. При тенденции неравномерного изменения значений зависимость носит название криволинейной.

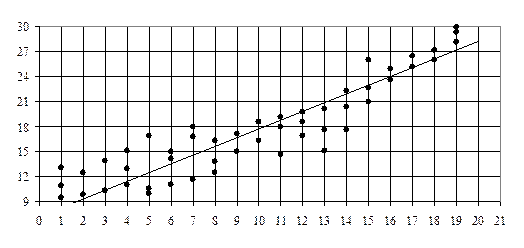
Рис. 1.3. Диаграмма рассеяния и линия регрессии

Линия на графике (см. рис. 1.3), изображающая тенденцию в изменении результативного признака при возрастании факторного, называется линией регрессии. В случае прямолинейной связи линия регрессии ищется в виде уравнения прямой линии:

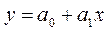, (1.23)

где у – теоретические значения результативного признака, образующие прямую линию; а₀, а₁ – параметры уравнения; х – значения факторного признака.

Во всех случаях расчет параметров уравнения производится методом наименьших квадратов. В основу метода положено требование минимальности отклонения теоретических значений у’_i от эмпирических (полученных в результате наблюдения) значений признака у_i при одном и том же значении х_i. Это требование в математических обозначениях записывается следующим образом:

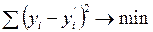. (1.24)

Подставляя вместо теоретических значений 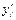их запись через параметры а₀ и а₁, получаем

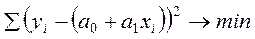. (1.25)

В этом выражении известны все х_i и у_i, полученные в результате наблюдения, неизвестны лишь а₀ и а₁. Полученная функция двух переменных а₀ и а₁ имеет минимум, когда частные производные 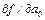и 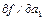одновременно равны 0. Произведя дифференцирование по а₀ и а₁, получаем систему двух уравнений с двумя неизвестными, решив которую, получим выражение для нахождения коэффициентов а₀ и а₁:

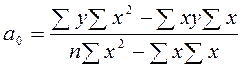, (1.26)

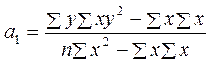, (1.27)

где n – общее число наблюдений; х, у – значения признаков, полученные в результате наблюдения.

2. Задание на контрольную работу

Date: 2015-07-24; view: 641; Нарушение авторских прав