
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Критерий устойчивости Михайлова
Из выражения (6) следует, что если все корни характеристического уравнения лежат в левой полуплоскости, т.е. m=0, то
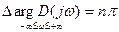 .
.
Отсюда следует первая формулировка критерия Михайлова.
Система автоматического управления устойчива, если при возрастании частоты от -¥ до +¥ изменение аргумента вектора D(jw) будет равно np, где n - порядок характеристического уравнения.
Вектор D(jw) можно представить в виде
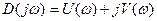 .
.
Вещественная составляющая этого выражения является четной функцией, а мнимая - нечетной функцией частоты, т.е. U(-w)=U(w);V(-w)= -V(w) и D(- jw)=U(w) - jV(w).
Отсюда следует, что кривая Михайлова симметрична относительно вещественной оси, и при ее построении можно ограничиться диапазоном частот от 0 до + ¥. Изменение аргумента вектора D(jw) при этом уменьшится в два раза и формулировка критерия Михайлова будет следующей.
Система автоматического управления устойчива, если при возрастании частоты от 0 до +¥ вектор D(jw) повернется на угол np/2 или, что то же самое, если кривая Михайлова при том же изменении частоты, начиная с положительной вещественной полуоси, обходит последовательно в положительном направлении n квадрантов и заканчивается в n-м квадранте (рис.6).
Если хотя бы один квадрант пропущен (рис.7), то система неустойчива.
Наблюдая за поведением кривой Михайлова для устойчивой САУ, можно заметить, что при ее прохождении через n квадрантов корни уравнений U(w)=0 и V(w)=0 чередуются между собой, т.е. между двумя корнями уравнения V(w)=0 лежит один корень уравнения U(w)=0.
Система автоматического управления устойчива, если корни уравнений V(w)=0 и U(w)=0 вещественные и перемежаются между собой.
Система может находиться на границе устойчивости и этому соответствуют два случая:
1) характеристическое уравнение системы имеет один нулевой корень, что будет при аn = 0;кривая Михайлова при этом выходит из начала координат;
2) характеристическое уравнение имеет пару чисто мнимых корней 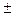 jwk и D(jwk)=U(wk)+jV(wk)=0, что может быть только, если одновременно U(wk)=0 и V(wk)=0; это означает, что кривая Михайлова проходит через начало координат.
jwk и D(jwk)=U(wk)+jV(wk)=0, что может быть только, если одновременно U(wk)=0 и V(wk)=0; это означает, что кривая Михайлова проходит через начало координат.
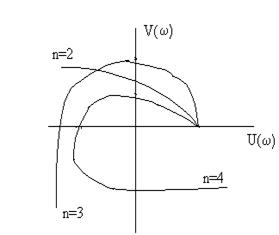
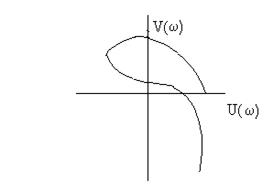
Рис. 6. Кривые Михайлова для Рис. 7. Кривая Михайлова для
устойчивых САУ неустойчивой САУ
Пример. Используя критерий Михайлова, оценить устойчивость системы
Пусть характеристическое уравнение замкнутой системы имеет вид
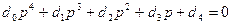 .
.
Сделаем замену p=jw и выделим вещественную и мнимую части
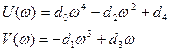 .
.
Построенная при заданных ранее параметрах системы кривая Михайлова имеет вид, показанный на рис.8.
Кривая начинается на вещественной положительной полуоси, проходит последовательно 4 квадранта и заканчивается в 4-м квадранте. Следовательно, при данных параметрах исследуемая система устойчива.
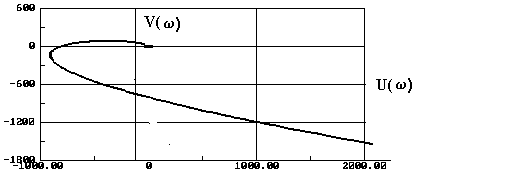
Рис. 8. Годограф Михайлова
Критерий устойчивости Найквиста
Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по виду АФЧХ разомкнутой системы.
Пусть передаточные функции разомкнутой и замкнутой системы имеют вид: 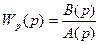 ;
; 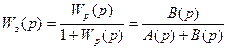 .
.
Введем функцию
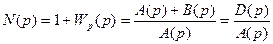 ,
,
где D(p) - характеристический полином замкнутой системы. Перейдя к частотным представлениям, получим
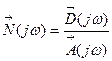 .
.
Вектор N(jw) называется вектором Найквиста. Очевидно, что числитель и знаменатель этого вектора имеют один и тот же порядок n. При использовании критерия Найквиста следует различать два случая.
1) Разомкнутая система устойчива и ее характеристическое уравнение A(p)=0 имеет все корни в левой полуплоскости. Тогда при изменении частоты от 0 до ¥
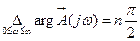 .
.
Изменение аргумента вектора D(jw) в общем случае равно
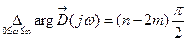 ,
,
где m - число корней уравнения D(p)=0, лежащих в правой полуплоскости.
Изменение аргумента вектора Найквиста будет
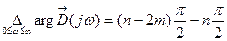 .
.
Если замкнутая система устойчива, то m=0 и
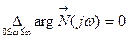 .
.
Так как при w®¥,W(jw)®0, то N(jw)®1. Рассмотрим рисунок 9,а, где изображена кривая Найквиста, которая описывается вектором Найквиста при изменении частоты от 0 до ¥. Нетрудно убедиться, что вектор Найквиста опишет угол, равный нулю только в случае, если его годограф не охватывает начало координат. Перенесем начало координат в точку с координатами (1,j0) (рис.9,б). Можно убедиться, что изменение аргумента вектора Найквиста будет равно нулю если АФЧХ Wр(jw) разомкнутой системы не охватывает критическую точку с координатами (-1,j0).






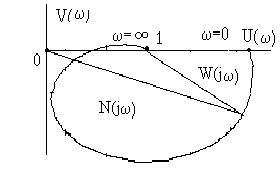
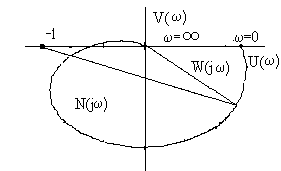
а) б)
Рис. 9. К определению критерия Найквиста
Критерий Найквиста для рассматриваемого случая формулируется следующим образом.
Система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчивой и в замкнутом состоянии, если АФЧХ Wр(jw) разомкнутой системы при изменении частоты от 0 до ¥ не охватывает критическую точку с координатами (-1, j0).
Особенности возникают, если разомкнутая система нейтрально-устойчива, т.е.
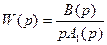 ,
,
где полином A1(s) имеет все корни в левой полуплоскости. При w=0 АФЧХ разомкнутой системы W(jw)=¥ и проследить поведение кривой АФЧХ в окрестности этой точки невозможно. При изменении частоты от -¥ до +¥ наблюдается движение корней вдоль мнимой оси снизу вверх и при w=0 происходит бесконечный разрыв. При этом движении обойдем нулевой корень (рис.10) по полуокружности бесконечно малого радиуса r так, чтобы этот корень остался слева, т.е. искусственно отнесем его к левой полуплоскости.



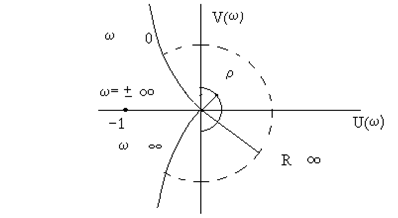
Рис. 10. Годограф Найквиста для нейтрально- устойчивой САУ
При движении по этой полуокружности в положительном направлении независимая переменная изменяется по закону
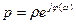 ,
,
где фаза j(w) изменяется от - p/2 до + p/2. Подставив это выражение в передаточную функцию вместо множителя p в знаменателе, получим
 ,
,
где R®¥ при r®0, а фаза j(w) изменяется от +p/2 до - p/2. Следовательно, в окрестности нулевого корня годограф W(jw) представляет собой часть окружности бесконечно большого радиуса, движение по которой происходит при увеличении частоты в отрицательном направлении.
Для оценки устойчивости замкнутой системы, если разомкнутая система нейтрально устойчива, необходимо АФЧХ W(jw) разомкнутой системы дополнить дугой бесконечно большого радиуса, начиная с меньших частот, в отрицательном направлении и для полученной замкнутой кривой воспользоваться критерием Найквиста для систем, устойчивых в разомкнутом состоянии.
2) Разомкнутая система неустойчива. В этом случае
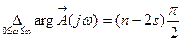 ,
,
где s - число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости. Если замкнутая система устойчива, т.е. m=0, то
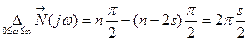 ,
,
т.е. АФЧХ разомкнутой системы охватывает критическую точку (-1,j0) в положительном направлении ровно s / 2 раз.
Система, неустойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если АФЧХ W(j сw) разомкнутой системы при изменении частоты от 0 до ¥ охватывает критическую точку (-1,j0) в положительном направлении ровно s/2 раз, где s - число правых полюсов разомкнутой системы.
Определение числа охватов критической точки - непростая задача, особенно в случае систем высокого порядка. Поэтому в практических приложениях нашла применение другая формулировка критерия Найквиста для рассматриваемого случая.
Переход годографа W(jw) через отрезок вещественной полуоси (-¥,-1), т.е. левее критической точки при увеличении частоты сверху вниз считается положительным, а снизу вверх - отрицательным.
Система, неустойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если разность между числом положительных и отрицательных переходов АФЧХ разомкнутой системы равна s/2. т.е.
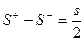 ,
,
где 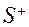 - число положительных переходов,
- число положительных переходов, 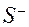 - число отрицательных переходов.
- число отрицательных переходов.
Определение запасов устойчивости по годографу Найквиста
Допустим, что АФЧХ некоторой разомкнутой системы имеет вид, показанный на рис. 11.
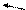

Рис. 11. АФЧХ разомкнутой системы
Угол g, образуемый прямой, проходящей через точку пересечения АФЧХ с окружностью единичного радиуса, что соответствует частоте среза системы, и отрицательной вещественной полуосью называется запасом устойчивости системы по фазе и равен
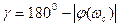 .
.
Date: 2015-07-24; view: 726; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |