Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Эпюры продольных усилий
|
|
Брус, работающий преимущественно на растяжение-сжатие называется стержнем.
Правило знаков. Продольная сила N считается положительной, если
вызывает растяжение, и отрицательной, если вызывает сжатие.
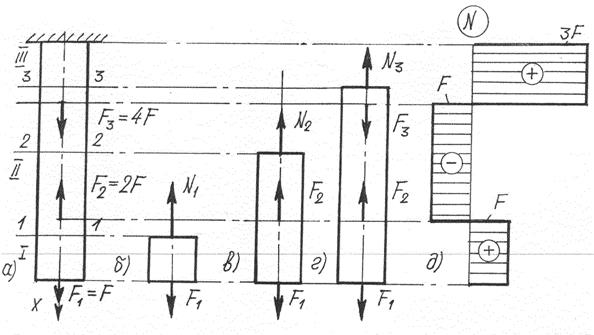Особенности построения эпюр рассмотрим на конкретном примере. Построим эпюру продольных усилий для стержня, расчетная схема которого изображена на рис. 3, а.
Рис. 3
Разбиваем стержень на участки, используя правила:
1) движемся со свободного конца;
2) границами участков являются сечения, в которых приложены внешние силы.
Рациональнее отбрасывать верхнюю часть, тогда нет необходимости определять реакцию опоры.
Проводим произвольное сечение 1-1 на 1-м участке (рис.3, б) и
рассматриваем равновесие нижней отсеченной части;
Σ X =0: F 1 - N 1= 0, отсюда следует N 1 = F 1 = F.
Искомые продольные усилия Ni всегда направляем на растяжение, т. е. в положительную сторону. Для определения продольных усилий нет необходимости каждый раз изображать отсеченную часть и записывать уравнение равновесия. Можно сразу записывать выражение для продольного усилия, как алгебраическую сумму проекций на ось бруса внешних сил, приложенных по одну сторону от рассматриваемого сечения.
2-й участок (рис. 3, в): N 2 = F 1- F 2 = F - F 2 = - F.
Знак минус указывает, что фактическое направление силы N 2 противоположно первоначально выбранному, т.е. 2-й участок испытывает сжатие.
3-й участок (рис. 3, г): N 3 = F 1 - F 2 + F 3 = F- 2 F + 4 F = З F, По полученным значениям строим эпюру, показанную на рис. 3, д. Положительные значения откладываем вправо, а отрицательные – влево от оси.
Правило: В местах приложения сосредоточенных сил на эпюре получаются "скачки". Размер "скачка" равен приложенной в этом сечении силе. Направление "скачка" связано с направлением действия силы.
Замечание. Скачкообразные изменения координат N носят условный характер, так как условно и само понятие "сосредоточенная сила". Фактическая внешняя сила распределена по некоторой небольшой части длины бруса; в пределах этой части значения N изменяется по некоторому закону, установить который не предоставляется возможным. Не известный криволинейный переходный участок эпюры заменяют условным "скачком". На вопрос: чему равна продольная сила в точке приложения F 2, ответить прямо нельзя. Можно лишь сказать, что бесконечно близко к точке справа N = + F, а бесконечно близко к точке сверху N = - F.
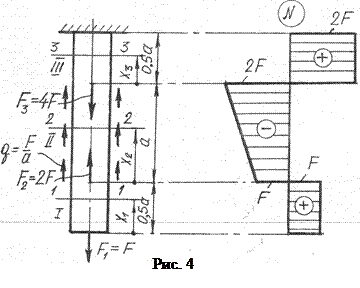Рассмотрим следующий пример. Построим эпюру продольных усилий бруса, изображенного на рис. 4. Отличие от предыдущего примера - наличие равномерно распределенной нагрузки интенсивностью q = F/а.
Участки остаются те же, но должна быть задана, длинна участков. 1 участок: 0 ≤ x 1 ≤ 0,5 а:
N 1= F.
2 участок 0 ≤ x 2 ≤ а:
N 2 = F - 2 F - qx 2.
Это уравнение прямой линии, поэтому для построения эпюры достаточно определить значение N в начале и в конце участка:
При х 2 = 0 получим N 2 = - F; при х 2 = а получим N 2 = F -2 F –F = -2 F.
Правило: На участке, где действует распределенная нагрузка, на эпюре – наклонная прямая.
3 участок: 0 ≤ x 2 ≤ 0,5 а: N 3 = F - 2 F + 4 F – qa = 2 F
4. Эпюры крутящих моменто в
Брус, работающий преимущественно на кручение, называется валом.
Правило знаков. Знак крутящего момента не имеет физического смысла, но для определенности при построении эпюр условимся о следующем правиле знаков.
Будем считать крутящий момент положительным, если при взгляде со стороны сечения, он представляется направленным по часовой стрелке (рис. 5).
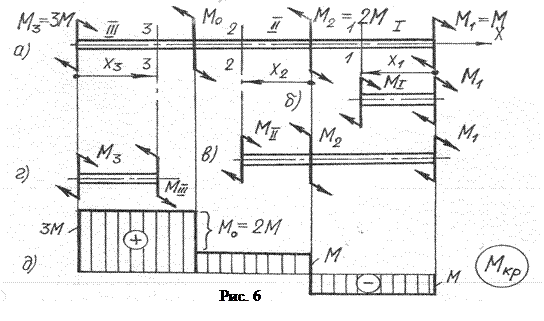В соответствии с международными рекомендациями крутящие моменты обозначаются: Те - внешний крутящий момент ( от torsion external); Тi -внутренний крутящий момент (от torsion inside). Построим эпюру крутящих моментов для вала, расчетная схема которой изображена на рис. 6, а.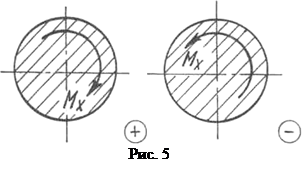 
Момент Мо не задан, его можно определить из уравнения равновесия Σ Мх = 0, но рациональнее вести построение эпюры, двигаясь со свободных концов слева, а затем справа. Величину Мо можно будет определить по построенной эпюре без вычислений. Разбиваем вал на 3 участка. Используем метод сечений, рассматривая равновесие оставленной части (рис. 6, б, в, г), приходим к выводу, что внутренние силы, возникающие в поперечном сечении вала, должны дать крутящий момент, уравновешивающий внешние моменты, приложенные к оставленной части.
Проводим произвольные сечения на каждом из 3-х участков и рассматривая равновесие отсеченных частей, получим:
1 участок: М I = - М 1 = - М;
2 участок: М II= - М 1 + М 2 = - М + 2 М = М;
3 участок: М III = М 3 = З М.
По полученным значениям строим эпюру, представленную на рис. 6, д.
5. Дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом. Особенности эпюр поперечных сил и изгибающих моментов
Построение эпюр Q и Мизг существенно упрощается при использовании дифференциальных зависимостей между q, Q, Мизг. Для вывода этих зависимостей выделим из балки двумя поперечными сечениями, расстояние между которыми равно dх, бесконечно малый элемент (рис. 7).
Распределенную нагрузку q направляем вверх, так как это направление считаем положительным.
В общем случае q может быть не равномерной, но из-за малости dх неравномерность не учитывается.
Спроецируем действующие на элемент силы на ось Оу:
Σ Y = 0: Qу + qdх - (Qу + dQу) = 0; получим:
dQy/dx = q.
Производная от поперечной силы по длине балки ровна интенсивности распределенной нагрузки.
Определим сумму моментов относительно точки К;
Σ Мк = 0: Мz + Qуdх + qdx dx/2 - (Мz + dМz) = 0, пренебрегая малыми второго порядка, получим:
dMz/dx = Qy.
Производная от изгибающего момента по длине балки равна поперечной силе.
Из этих зависимостей следует:
d2Mz/dx2 = q.
Интенсивность распределенной нагрузки равна второй производной от изгибающего момента по длине балки.
В сложных случаях нагружения балок эпюры Q и Мизг целесообразнее строить без записи аналитических выражений Q (х), Мизг (х) по участкам, вычисляя значения Q, Мизг только в характерных точках - это границы участков и лишь в отдельных случаях - промежуточные сечения. При таком построении используется ряд правил, которые являются следствием из полученных дифференциальных зависимостей:
1. На участках, где нет распределенной нагрузки q:
- эпюра Q - прямая, параллельная базе, т.е. Q = сonst,
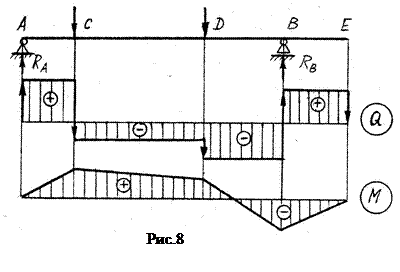
- эпюра Мизг - наклонная прямая (рис. 8).
2. На участках, где приложена равномерно распределенная нагрузка q:
- эпюра Q - наклонная прямая,
- эпюра Мизг - парабола (кривая второго порядка) с выпуклостью, направленной против направления q (рис. 9).
3. Если на участке:
а) Q > 0, то Мизг возрастает (рис. 8, участки АС и ВЕ);
б) Q < 0, то Мизг убывает (рис. 8, участки СD и DC);
в) Q = 0, то Мизг = сonst (чистый изгиб).
4. Если на эпюре Q наклонная прямая проходит через нулевое значение, то Мизг - в этом сечении имеет экстремальное значение (min или maх) (рис. 9, сечение С).
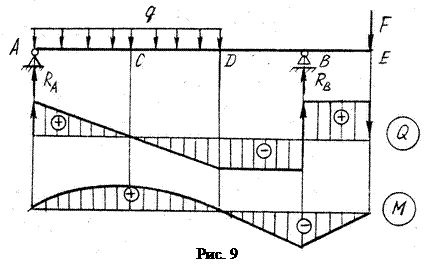
dM/dx = 0 - признак экстремума - касательная к эпюре параллельна оси.
5. Под сосредоточенной силой:
- на эпюре Q - скачок в направлении действия силы, равный по величине этой силе (на рис. 8, 9 эти скачки отмечены толстыми линиями со стрелками);
- на эпюре Мизг - излом, острие излома направленно против направления силы (на рис. 8 – сечения C, D и В; на рис. 9 – сечение В).
6. В точках, соответствующих началу и концу участка действия распределенной нагрузки, парабола и прямая линия эпюры Мизг сопрягаются плавно, если в указанных точках не приложено сосредоточенных сил (рис. 9 – сечение D).
7. В сечениях, где приложены сосредоточенные моменты, на эпюре Мизг будут скачки на величину этих моментов и в направлении, соответствующем знаку момента. На эпюре Q - никаких изменений.
8. На свободном или шарнирно-опертом конце балки Мизг = 0, если там не приложен сосредоточенный момент, а Q равна внешней сосредоточенной силе (активной или реактивной).
9. В заделках Q и Мизг численно равны опорной реакции и реактивному моменту.
10. Q равна тангенсу угла наклона касательной к оси на эпюре Мизг в данном сечении.
11. Изменение величины Мизг на каком-либо участке балки равно площади эпюры Q на этом участке плюс сосредоточенные моменты, действующие на этом участке.
12. Изменение величины Q на каком-либо участке балки равно площади эпюры q на этом участке.
Проиллюстрируем использование этих правил на примерах, представленных ниже.
Date: 2015-07-24; view: 1962; Нарушение авторских прав