
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод Гаусса. Рассмотрим на простейшем примере известный со школы способ исключения неизвестных при решении систем уравнений
Рассмотрим на простейшем примере известный со школы способ исключения неизвестных при решении систем уравнений. Пусть дана система:
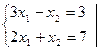
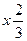
Умножим первое уравнение на такой коэффициент 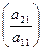 , чтобы в обоих уравнениях коэффициент при х 1 стал бы одинаковым
, чтобы в обоих уравнениях коэффициент при х 1 стал бы одинаковым
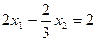
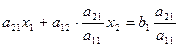
Теперь вычтем его из второго уравнения, т.е.
-2 х 1+ х 2=7
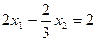
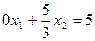
Мы выполнили операцию исключения неизвестной х 1 из второго уравнения. Запишем систему уравнения после этого исключения в следующем виде. Первое уравнение записываем в исходном виде.
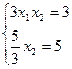
Второе уравнение содержит лишь одно неизвестное, которое легко вычисляется х 2=3. Подставив полученное значение х 2 в первое уравнение, можем вычислить и первое неизвестное х 1.
Проведенные действия и составляют сущность метода Гаусса. Рассмотрим преобразования по методу Гаусса для системы уравнений n -го порядка.
| а 11 х 1+ а 12 х 2+ … + а 1 nхn = b 1 |
| 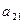
| 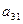
| 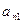
| |||
| а 21 х 1+ а 22 х 2+ … + а 2 nхn = b 2 | 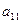
| 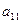
| 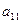
| ||||
| а 31 х 1+ а 32 х 2+ … + а 3 nхn = b 3 | |||||||
| … … … … | |||||||
| аn 1 х 1+ аn 2 х 2+ … + аnnхn = bn |
Вычтем из второго уравнения первое, умноженное на 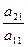 .
.
При этом во втором уравнении будет уничтожен коэффициент при х 1.
Затем из третьего уравнения также вычтем первое, умноженное на 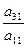 .
.
Проделав аналогичные преобразования с остальными уравнениями системы, превратим в нуль все коэффициенты первого столбца, кроме элемента а 11. Получим следующую систему:
| а 11 х 1+ а 12 х 2+ а13 х 3+… + а 1 nхn = b 1 | 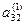
| … | 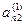
|
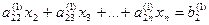
| 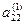
| 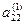
| |
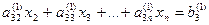
| |||
| … … … … | |||
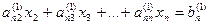
|
Затем при помощи второго уравнения преображенной системы исключим из третьего, четвертого и т.д. уравнений коэффициенты второго столбца лежащие ниже 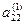
а 11 х 1+ а 12 х 2+ а13 х 3+… + а 1 nхn = b 1
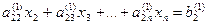
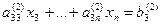
… … …
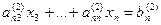
Последовательно продолжая этот процесс, исключим из системы все коэффициенты, лежащие ниже главной диагонали. В результате получим треугольную систему уравнений.
а 11 х 1+ а 12 х 2+ а 13 х 3+… + а 1 nхn = b 1
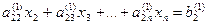
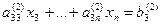
… … …
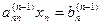
Процесс получения треугольной системы называется “прямым ходом” по методу Гаусса. Треугольная система легко решается “обратным ходом”. Из последнего уравнения определяется последнее неизвестное 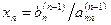 . Затем из предпоследнего уравнения постановкой найденного значения хn определяется хn -1. После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных х i (i = 1, …, n).
. Затем из предпоследнего уравнения постановкой найденного значения хn определяется хn -1. После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных х i (i = 1, …, n).
При решении системы линейных уравнений методом Гаусса все вычисления можно поместить в следующую таблицу. Рассмотрим таблицу на примере решения системы уравнений третьего порядка.
| № шага преобразований | х х 1 | х х 2 | х х 3 | ||
| 1) |  а 11 а 11
| а 12 | а 13 | b 1 |  : а 11 : а 11
|
| а 21 | а 22 | а 23 | b 2 | ||
| а 31 | а 32 | а 33 | b 3 | ||
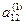
| 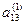
| 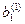
| |||
| 1 2) |  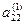
| 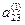
| 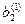
| 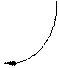 : : 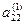
| |
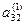
| 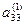
| 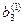
| |||
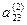
| 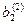
| ||||
| 2 3) | 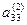
| 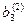
|  : : 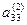
| ||
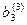
|
Уравнения 1), 2) и 3) составляют искомую треугольную матрицу после “прямого хода”. Число шагов преобразований в “прямом ходе” методом Гаусса равно n -1.
Коэффициенты а 11, 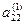 ,
, 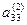 - называются “ведущими” элементами.
- называются “ведущими” элементами.
При “обратном ходе” можно использовать строки таблицы, содержащие единицы, т.е. вспомогательные уравнения. Имеем 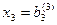 далее
далее
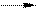
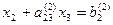
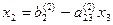
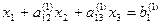
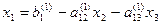
ПРИМЕР:
| № шага | х 1 | х 2 | х 3 | B | ||
| : 4 | ||||||
| 0,25 | 0,5 | х 2 | х 1 | |||
| 7,5 | ||||||
| 1,75 | 3,5 | |||||
| 0,4 | 3,2 | х 1,75 | ||||
| 2,8 | 8,4 | |||||
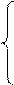 Треугольная система
Треугольная система
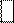 4 х 1+ х 2+2 х 3=12
4 х 1+ х 2+2 х 3=12
 7,5 х 2+3 х 3=24
7,5 х 2+3 х 3=24
 2,8 х 3=8,4
2,8 х 3=8,4
или
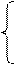 х 1+0,25 х 2+0,5 х 3=3
х 1+0,25 х 2+0,5 х 3=3
х 2+0,4 х 3=3,2
х 3=3
Обратный ход
х 2=3,2-0,4∙3=2
х 1=3-0,25∙2-0,5∙3=1
Вычисление определителя методом Гаусса
(третий способ, без вывода)
Определитель матицы А равен произведению всех “ведущих” элементов при преобразовании ее по методу Гаусса.
Для вычисления определителя матрицы А выполняется только “прямой” ход методом Гаусса, причем столбец свободных членов В становится излишним.
ПРИМЕР: дана матрица
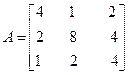 det А =4∙7,5∙2,8=84
det А =4∙7,5∙2,8=84
 Вычисление обратной матрицы методом Гаусса
Вычисление обратной матрицы методом Гаусса
А ∙ А -1 = Е
Матрицы А и Е известны, требуется определить А -1. Обозначим столбцы матрицы А -1 через х 1, х 2, …, хn т.е.
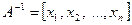
Столбцы для матрицы Е обозначим через Е 1, Е 2, …, Еn
Тогда можем записать n систем уравнений
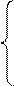 Ах 1= Е 1
Ах 1= Е 1
Ах 2= Е 2
Ахn = Еn
Развернем первое матричное уравнение Ах 1= Е 1
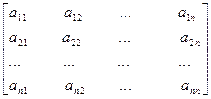 х
х 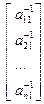 =
= 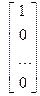
Другие матричные уравнения аналогичны.
Следовательно, для получения обратной матрицы А -1 достаточно выполнить n решений методом Гаусса систем линейных уравнений с разными правыми частями - y столбцами матрицы Е.
Полученные решения х 1, х 2, …, хn будут столбцами искомой обратной матрицы А -1.
Трангуляции матрицы
Квадратную матрицу А можно представить как произведение двух треугольных матриц А=LW, где
L – нижняя треугольная матрица,
W – верхняя треугольная матрица.
Матрица W вычисляется при прямом ходе Гаусса
а 11 а 12 а 13 … а 1 n
0 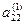
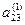 …
… 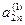
0 0 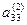 …
… 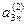
… … … … …
0 0 0 … 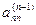
У матрицы L наоборот все элементы выше главной диагонали нулевые. Остальные элементы матрицы L вычисляются в результате деления элементов по столбцам, полученных при том же прямом ходе Гаусса, на ведущие элементы. Сначала вычисляются элементы первого столбца матрицы L делением на ведущий элемент а 11, затем после первого шага “прямым ходом” метода Гаусса вычисляются элементы второго столбца, начиная с диагонального, делением на ведущий элемент а 11 и т.д.
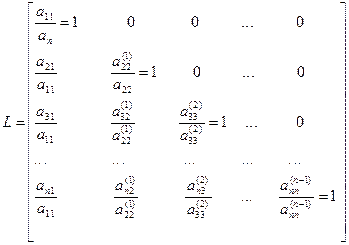
Требуется решить системы уравнений
Ах = В
Так как А = LW то LWх = В
Обозначим Wх = Z
Тогда вместо системы Ах = В можем записать ей эквивалентную
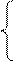 LZ = В
LZ = В
Wx = Z (5)
Решение эквивалентной системы с треугольными матрицами L и W занимает гораздо меньше времени, чем решение исходной системы Ах = В. Это обстоятельство очень важно при необходимости решать систему уравнений многократно при одной и той же матрице А и разных векторах свободных членов В, что обычно имеет место при расчетах режимов работы электрических систем. Триангуляция же матрицы А проводится только один раз.
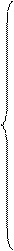 То есть элементы матрицы А – это, как правило, параметры схемы замещения эл. системы, В – вектор узловых токов или мощностей. Часто ставится задача определения параметров большего числа режимов при изменении токов или мощностей потребителей в узлах при неизменной схеме замещения. Если триангуляция матрицы А осуществлена, то можно быстро пользуясь системой (5) посчитать необходимые режимы, меняя в этой системе вектор В. Для каждого режима сначала решается треугольная подсистема LZ = В относительно Z последовательной подстановкой в уравнения подсистемы найденных значений неизвестных из предыдущих уравнений, начиная с Z 1
То есть элементы матрицы А – это, как правило, параметры схемы замещения эл. системы, В – вектор узловых токов или мощностей. Часто ставится задача определения параметров большего числа режимов при изменении токов или мощностей потребителей в узлах при неизменной схеме замещения. Если триангуляция матрицы А осуществлена, то можно быстро пользуясь системой (5) посчитать необходимые режимы, меняя в этой системе вектор В. Для каждого режима сначала решается треугольная подсистема LZ = В относительно Z последовательной подстановкой в уравнения подсистемы найденных значений неизвестных из предыдущих уравнений, начиная с Z 1
Z 1 = b 1
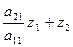 = b 2
= b 2
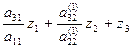 = b 3
= b 3
… … … … …
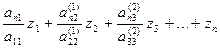 = bn
= bn
Значение Z 1 уже известно из первого уравнения, Z 2 определяется из второго уравнения подстановкой в него значения Z 1 и т.д. Определяются все Z. Затем аналогично решается вторая треугольная подсистема Wx = Z путем обратной подстановки, начиная с хn (аналогично обратному ходу методом Гаусса).
Метод Жордана-Гаусса
Метод Жордана-Гаусса называют еще методом Гаусса без обратного хода. Сущность его состоит в том, что на втором шаге переменная исключается из всех уравнений, кроме второго, на третьем шаге исключается также из всех уравнений, кроме третьего и т.д. После шагов в каждом уравнении остается одна неизвестная, т.е. получим решение системы таким образом, исключение переменных по методу Жордана-Гаусса эквивалентно преобразованию матрицы коэффициентов в единичную. Рассмотрим таблицу вычислений по методу Жордана-Гауса.
| № шага преобразований | A | C | B | ||
| а 11 | a 12 | … | a 1 n | b 1 | |
| а 21 | a 22 | … | a 2 n | b 2 | |
| а 31 | a 32 | … | a 3 n | b 3 | |
| … | … | … | … | … | |
| аn 1 | an 2 | … | ann | bn | |
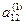
| … | 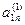
| 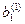
| ||
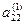
| … | 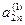
| 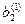
| ||
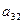
| … | 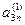
| 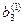
| ||
| … | … | … | … | … | |
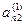
| … | 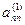
| 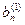
| ||
| … | … | … | … | … | … |
| n | … | 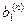
| |||
| … | 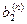
| ||||
| .. | .. | … | … | ||
| … | 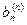
|
Нахождение обратной матрицы методом Жордана-Гаусса
 Рассмотрим вычислительную процедуру определителя А-1 на конкретном примере.
Рассмотрим вычислительную процедуру определителя А-1 на конкретном примере.
А∙А -1= Е
Пусть
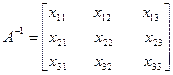
А х 1 х 2 х 3 Е 1 Е 2 Е 3
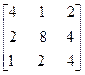 х
х 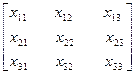 =
= 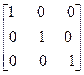
| № шага преобразования | х х 1 | х х 2 | х х 3 | Е 1 | Е 2 | Е 3 |
| 0,25 | 0,5 | 0,25 | ||||
| 7,5 | -0,5 | |||||
| 1,75 | 3,5 | -0,25 | ||||
| 0,4 | 0,2667 | -0,0333 | ||||
| 0,4 | -0,0667 | 0,1333 | ||||
| 2,8 | -0,1333 | -0,2333 | ||||
| 0,2857 | -0,1428 | |||||
| -0,0477 | 0,1666 | -0,1428 | ||||
| -0,0476 | -0,0833 | 0,357 |
Проверка:
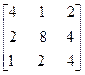 х
х 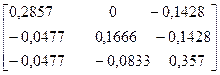 =
= 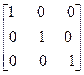
По такой же вычислительной схеме можно вычислять значения переменных х 1, х 2, х 3, …, х при одной матрице коэффициента А и разных столбцах свободных членов В 1, В 2, В 3, …, Вn.
Недостатки метода Гаусса (его недостатки и способы их устранения)
1. Если определитель матрицы А мал, то из-за ошибок округлений сильно снижается точность получения искомых корней.
2. Метод Гаусса требует, чтобы диагональные элементы в процессе исключения переменных не были равны нулю (т.к. строки делятся на них). Поэтому часть применяют метод Гаусса с выбором главного элемента, который заключается в следующем. При обращении в нуль элементов первого столбца из всей матрицы выбирается наибольший элемент и затем в нуль элементы второго столбца, рассматривается сокращенная матрица (путем вычеркивания в уже полученной системе первого уравнения) и в ней наибольший элемент переставляется на ее первое место и т.д.
3. Метод Гаусса требует большего объема памяти ЭВМ по сравнению с итерационными методами. Существуют различные приемы по сокращению занимаемой памяти ЭВМ при решении методом Гаусса электроэнергетических задач.
Например, необходимо решить систему
Yy ∙ Uy = Iy
при использовании метода узловых напряжений.

Перенумерация
- Экономичность памяти
- Сокращение времени счета
| Y= | → | |||||||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | ||||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | |||||||||||||||||||||
| + | + | + | + | + | + | + | + | |||||||||||||||||
| + | + | + | + | + | + | + | ||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | + | + | + | |||||||||||||||||
| + | + | + | + | + |
(30 х 70)
Я=10 х 10=100 Я=52 (26)
В ряде случаев для нахождения корней системы линейных уравнений удобнее пользоваться приближенными итерационными методами (или методами последовательных приближений).
Date: 2015-07-24; view: 472; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |