
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула Гаусса
Пусть необходимо вычислить определённый интеграл вида:
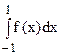
где f(x) – имеет высокую степень гладкости на интервале [-1; 1].
Данную задачу можно решить с помощью квадратурной формулы
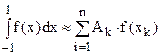 .
.
Гауссом было доказано, что для достижения наивысшей точности результата интегрирования необходимо в качестве узлов квадратурной формулы взять корни многочлена Лежандра
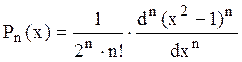 .
.
Коэффициенты Ак при этом вычисляются по формулам
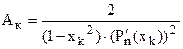 .
.
Рассмотрим применение этих формул.
При n=1 имеем одну узловую точку внутри отрезка [-1; 1], которая определяется из уравнения

Т.к. 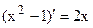 , то узловую точку находим из уравнения
, то узловую точку находим из уравнения 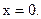 Отсюда
Отсюда 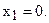
Т.к. 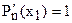 , то
, то 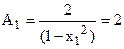 .
.
При n=2 получаем две узловые точки внутри отрезка [-1; 1], которые определяется из уравнения
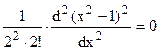
Преобразовав его получаем
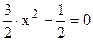 .
.
Его решение 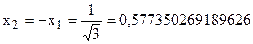 . Т.к.
. Т.к. 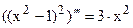 ,
,
то общая формула для вычисления квадратурных коэффициентов приобретёт вид 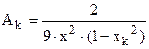 . Подставляя узловые точки, получаем:
. Подставляя узловые точки, получаем:
при 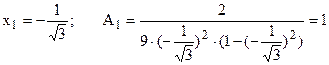 ;
;
при 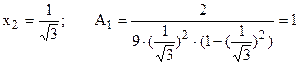 .
.
Для различного числа разбиения отрезка [-1; 1] можно получить таблицу узлов xk и коэффициентов Ak. (Как это сделать будет показано на практическом занятии)
| К-во точек разбиения | Узлы квадратурной формы | Коэффициенты квадратурной формы |
| n=1 | x1=0 | A1=2 |
| n=2 | 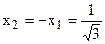
| 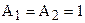
|
| n=3 | 
| 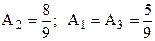
|
| n=4 | 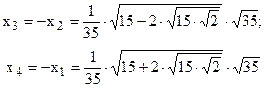
|
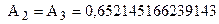
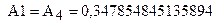
|
| n=5 | 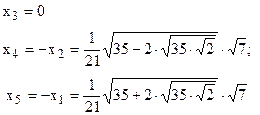
| 
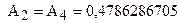
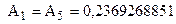
|
В случае произвольного интервала интегрирования [a; b] (когда он не совпадает с отрезком [-1; 1]) предварительно делают замену переменной
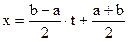
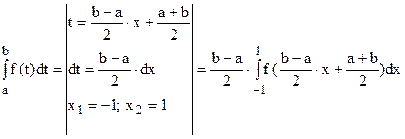 .
.
А уже к преобразованному интегралу можно применить формулу Гаусса. Получим
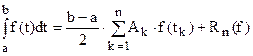 ,
,
где 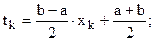
 – узлы квадратурной формулы Гаусса;
– узлы квадратурной формулы Гаусса;
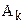 – соответствующие коэффициенты;
– соответствующие коэффициенты;
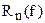 – остаток квадратуры.
– остаток квадратуры.
Остаток квадратурной формулы Гаусса определяется по формуле
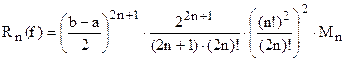
где 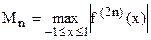
Пример. По формуле Гаусса вычислить интеграл I= 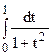 (при n=5).
(при n=5).
Решение.
Т.к. интервал интегрирования не совпадает с отрезком [-1; 1], применим
замену
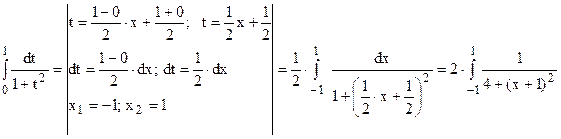 .
.
| <== предыдущая | | | следующая ==> |
| | | Борское, 2013 |
Date: 2015-07-24; view: 459; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |