Доказательство

Дополнение

К курсу «Дискретная математика для программистов»

Блоки

Изложение построено в форме дополнений к учебнику «Дискретная математика для программистов 3-е издание». Места дополнений указаны с помощью номеров параграфов учебника.

8.1.1.

ЛЕММА В любом нетривиальном связном графе G (V, E)

" U, W Ì V (U ¹Æ& W ¹Æ & U ÇW=Æ& U È W = V ® $ (u, w)Î E (u Î U & w Î W)).

8.1.2.

...

СЛЕДСТВИЕ 2 [к теореме 1]. Если граф G (V, E) связен, а вершина v не является точкой сочленения, то для любых двух других вершин u и w существует простая á u, w ñ -цепь, не содержащая вершину v.

Доказательство. Данное утверждение является отрицанием пункта 2 теоремы 1. 

...

Графы K ₁ и K ₂ формально можно считать блоками, поскольку у них нет точек сочленения. Эти блоки уместно назвать тривиальными, поскольку они удовлетворяют определению, но не обладают замечательными свойствами, присущими нетривиальным блокам. В частности, нетрудно видеть, что в нетривиальном блоке не только нет точек сочленения, но также нет мостов и нет висячих вершин. Более того, все вершины блока связана неединственным образом, что устанавливает следующая теорема.

ТЕОРЕМА 3. Если граф G (V, E) связен и p (G)>2, то следующие утверждения эквиваленты.

1. G – нетривиальный блок;
2. любые две вершины принадлежат одному простому циклу;
3. любая вершина и любое ребро принадлежат одному простому циклу;
4. любые два ребра принадлежат одному простому циклу;
5. для любых двух вершин и любого ребра существует простая цепь, соединяющая эти вершины и содержащая это ребро;
6. для любых трех вершин существует простая цепь, соединяющая две вершины и содержащая третью.

Доказательство

[1Þ2] Пусть u и w – любые две вершины. Рассмотрим U – множество всех вершин, входящих во все простые циклы, содержащие вершину u. Ясно, что U ¹Æ, поскольку вершина u не является висячей, поэтому для любых двух вершин u ₁ и u ₂, смежных с u, по следствию 2 существует соединяющая их цепь, не содержащая вершины u, и, значит, существует некоторый простой цикл, содержащий вершину u. Положим W:= V \ U. Далее от противного. Пусть W ¹Æ и w Î W. Граф связен, и значит в нем есть ребро (s, t), такое что s Î U, t Î W. Поскольку u Î U и s Î U, обе эти вершины принадлежат некоторому простому циклу Z. По следствию 2 существует простая á u, t ñ - цепь P, не содержащая вершину s. Обозначим через v первую вершину, считая от вершины t, на цепи P, которая также принадлежит циклу Z. Тогда рассмотрим следующую последовательность простых цепей: отрезок цепи P от вершины t до вершины v, отрезок цикла Z от вершины v до вершины u, отрезок цикла Z от вершины u до вершины s, ребро (s, t). Это цикл, причём простой, и вершины u и t обе принадлежат этому циклу и входят в множество U, что противоречит выбору вершины t и предположению w Î W.

Рис. К доказательству пункта [1Þ2] теоремы о блоках

[2Þ3] Пусть u – любая вершина и (v, w) – любое ребро. Вершины u и v принадлежат некоторому простому циклу Z. Если w Î Z, то требуемый цикл строится из ребра (v, w) и из того отрезка цикла Z от v до w, который содержит вершину u. Если же w Ï Z, то по следствию 2 существует простая á u, w ñ - цепь P, не содержащая вершину v. Обозначим через s первую вершину, считая от вершины w, на цепи P, которая также принадлежит циклу Z. Тогда рассмотрим следующую последовательность простых цепей: отрезок цепи P от вершины w до вершины s, отрезок цикла Z от вершины s до вершины v, содержащий вершину u, и ребро (v, w).

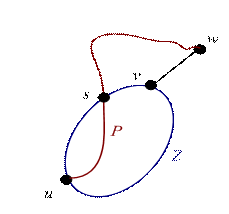
Рис. К доказательству пункта [2Þ3] теоремы о блоках

[3Þ4] Пусть (u, w) и (s, t)– два любых ребра. По условию, ребро (u, w) и вершина s принадлежат некоторому циклу Z ₁ и в то же время ребро (u, w) и вершина t принадлежат некоторому циклу Z ₂. Тогда рассмотрим следующую последовательность простых цепей: ребро (u, w), отрезок цикла Z ₁ от вершины u до вершины s, ребро (s, t), отрезок цикла Z ₂ от вершины t до вершины w.

Рис. К доказательству пункта [3Þ4] теоремы о блоках

[4Þ5] Пусть u и w – любые две вершины и (s, t) – любое ребро. Граф связен, значит, существует простая á u, w ñ - цепь P. Пусть á u, w ñ = (u, x, …, w). По условию, ребра (u, x) и (s, t) принадлежат некоторому простому циклу Z. Обозначим через v первую вершину, считая от вершины w, на цепи P, которая также принадлежит циклу Z. Тогда рассмотрим следующую последовательность простых цепей: отрезок цикла Z от вершины u до вершины v, проходящий через ребро (s, t), отрезок цепи P от вершины v до вершины w.

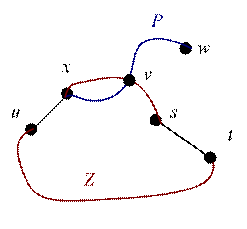
Рис. К доказательству пункта [4Þ5] теоремы о блоках

[5Þ6] Пусть u, v, w – любые три вершины и (w, x) – некоторое ребро, инцидентное w. По условию, существует простая á u, v ñ - цепь P, содержащая ребро (w, x) и, значит, вершину w.

[6Þ1] Пусть v – любая вершина. Покажем, что вершина v не является точкой сочленения, то есть что граф G – v связен. Рассмотрим u и w – любые две вершины. По условию существует простая á v, w ñ - цепь P, проходящая через вершину u. Отрезок цепи P от u до w обеспечивает связанность вершин u и w в графе G – v. 

8.1.3.

...

Особое значение имеют двусвязные графы по двум причинам. Во-первых, они особенно часто встречаются в приложениях, во-вторых, двусвязные графы являются частным случаем блоков, которые обладают многими полезными свойствами, часть из которых приведена в предыдущем параграфе.

Замечание. Легко видеть, что любой двусвязный граф является блоком, поскольку не содержит точек сочленения. В то же время, всякий нетривиальный блок является, по меньшей мере, двусвязным, но может быть и трехсвязным, и вообще иметь произвольную величину вершинной связности, поскольку, например, всякий полный граф является блоком.