Вращение в пространстве

Распространим математическое описание вращения, понятие момента количества движения, момента силы и т.д. на трехмерное пространство.

xF_y - yF_x так и остается моментом силы относительно оси z (плоскость вращения ху) и он равен скорости изменения момента импульса (xp_y - yp_x) относительно оси z:

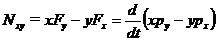ось z

Аналогично можно получить для оси х (плоскость вращения yz):

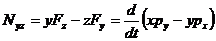ось х

Для оси у (плоскость вращения zx):

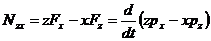ось у

Таким образом, имеются законы о том, что внешний момент сил в некоторой плоскости равен скорости изменения углового момента в этой плоскости.

А если повернуть оси, например, в плоскости х, у. Новые координаты назовем х ^/, у ^/. Новый момент сил в этой плоскости 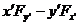. Найдем связь между новыми и старыми моментами. Это похоже на манипуляции с векторами. - Да. А не вектор ли момент сил? - Да. Докажем это.

Пусть ось z останется той же. Поворачиваем х и у на угол q. Законы преобразования координат мы рассматривали раньше:

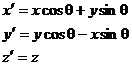
Поскольку сила является вектором, закон преобразования ее компонент такой же:

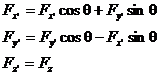
Подставляем уравнения преобразования координат и силы в выражения для моментов силы (промежуточные преобразования опускаем):

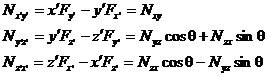
Можно увидеть связь между законами преобразования моментов силы и законами преобразования координат. Если назвать N_xy z -компонентой N_z вектора N, аналогично, если связать плоскость yz с х -компонентой новоиспеченного вектора N, а плоскость zx с у -компонентой, то закон преобразования будет выглядеть так:

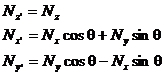
что в точности соответствует закону преобразования векторов.

Следовательно, доказано, что комбинацию xF_y - yF_x можно отождествить с тем, что обычно называется z -компонентой некоторого искусственно введенного вектора. Хотя момент сил является своего рода «кручением» в плоскости и, казалось бы, не имеет векторного характера, математически он все-таки ведет себя как вектор. Этот вектор направлен под прямым углом к плоскости кручения, а его длина пропорциональна силе кручения. Три компоненты такой величины будут преобразовываться при вращении системы координат как самый настоящий вектор.

Итак, мы представляем момент силы в виде вектора. Согласно правилу, с каждой плоскостью, в которой он действует, мы связываем прямую, перпендикулярную к этой плоскости. Однако перпендикулярность к плоскости оставляет неопределенный знак вектора. Чтобы определить его, необходимо еще одно дополнительное правило, которое говорило бы нам, что если момент силы действует определенным образом в плоскости ху, то соответствующий ему вектор направлен «вверх» по оси z. Предположим, что система координат хуz правосторонняя (если вращать ось х по направлению к оси у, то направление, связанного с таким вращением, поступательного движения винта с правовинтовой резьбой, укажет положительное направление оси z). Тогда правило должно быть таким: если представить себе кручение, как ввертывание болта с правовинтовой резьбой, то направление вектора, связанного с этим кручением, определяется поступательным движением болта.

Векторное произведение

В предыдущих рассуждениях совершенно несущественно, что х - координата, F -сила, а существенным является закон преобразования векторов. Значит, например, (a_xb_y - a_yb_x) можно связать с z -компонентой какого-то вектора с и т.д. Можно придумать для такой связи название и обозначение:

векторное произведение с = а ´ b = [ a, b ],

что расшифровывается:

c_x = a_yb_z - a_zb_y

c_y = a_zb_x - a_xb_z

c_z = a_xb_y - a_yb_x

Свойства векторного произведения

а ´ b = -b ´ a

Отсюда:

а ´ а = 0

Результатом векторного произведения есть вектор, который перпендикулярен обоим перемножаемым векторам: с ^ а, с ^ b. Доказательством является равенство нулю скалярных произведений с × а и с × b (скалярные произведения можно расписать как сумму произведений одноименных проекций векторов).

Модуль векторного произведения равен произведению модулей векторов на синус угла между ними: ÷ а ´ b ê= а b sina. Это правило легко доказывается путем вычисления результата векторного произведения через проекции векторов для простейшего частного случая: вектор а смотрит из начала координат в направлении оси х (а_y и a_z = 0; a_x = a), вектор b - расположен в плоскости ху (b_z = 0). Поскольку результат векторного произведения не зависит от выбора системы координат (это свойство любого вектора, для этого они и придуманы), правило можно распространить на произвольную систему координат.

Способ определения направления вектора, являющегося результатом векторного произведения: если вращать вектор а (первый из перемножаемых векторов) по направлению к вектору b (второй из перемножаемых векторов), то вектор c = а ´ b будет направлен в сторону поступательного движения, связанного с этим вращением, винта с правой резьбой. Это простая договоренность. Получается, что результатом векторного произведения является не совсем «честный» вектор. Такие вектора называются аксиальными, или псевдовекторами, в отличие от обычных полярных векторов. Аксиальные вектора хорошо передают свойства вращения.

Приводим без доказательства сводку правил векторной алгебры:

A×B =Скаляр=A_xB_x+A_yB_y+A_zB_z,

A´B =Вектор,

(A´B)_z=A_xB_y-A_yB_x,

(A´B)_x=A_yB_z-A_zB_y,

(A´B)_y=A_zB_x-A_xB_z,

A´A =0,

A× (A´B)=0,

A× (B´C)=(A´B) ×C,

A´ (B´C)= B (A×C)- C (A×B)