Задание 7

1. Все значения равномерно распределенной случайной величины принадлежат отрезку [2, 8]. Найти вероятность попадания случайной величины в отрезок [3, 5].

2. Найти среднее время безотказной работы устройства, если известно, что для данного устройства вероятность работы без сбоев в течение 100 часов равна 0,2. (Предполагается, что время безотказной работы распределено по экспоненциальному закону).

3. Время безотказной работы механизма подчинено показательному закону с плотностью распределения вероятностей 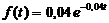при t > 0 (t – время в часах). Найти вероятность того, что механизм проработает безотказно не менее 100 часов.

4. Время простоя оборудования в ожидании ремонта распределено по показательному (экспоненциальному) закону с математическим ожиданием, равным 2 часа. Найти вероятность простоя более трех часов.

5. Предполагая, что время, необходимое для ремонта поступившего вагона, распределено по показательному (экспоненциальному) закону с параметром l =0,125 [час^-1], найти вероятность того, что для ремонта одного вагона понадобится не более шести часов.

6. В результате проверки точности работы прибора установлено, что 60% ошибок не вышло за пределы ±20 мм, а остальные ошибки вышли за эти пределы. Определите среднее квадратическое отклонение ошибок прибора, если известно, что систематических ошибок прибор не дает, а случайные ошибки распределены по нормальному закону.

7. Случайная величина распределена нормально с математическим ожиданием М[ ] =25 и дисперсией D[ ] =100. Напишите выражение для плотности вероятности f(x) и функции распределения F(x). Чему равна вероятность события 15£ £35?

8. Взвешивание на весах производится без систематических ошибок. Случайные ошибки имеют с дисперсию, равную 100 г². Полагая, что ошибки распределены по нормальному закону, определить вероятность того, что ошибка при взвешивании предмета по абсолютной величине не превысит 50 г.

9. Производится измерение вала без систематических ошибок. Случайные ошибки измерения подчинены нормальному закону распределения со средним квадратическим отклонением, равным 1 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 1,5 мм.

10. Автоматический станок производит однотипные изделия, номинальный размер которых равен 3 см. Фактический размер изделий имеет разброс, подчиненный нормальному закону с s[ ] =0,05 см. Систематические отклонения размера отсутствуют. При контроле отбраковываются все изделия, размер которых отличается от номинального больше, чем на 0,12 см. Определить, какой процент изделий в среднем будет отбраковываться.

11. Случайная величина распределена нормально с математическим ожиданием М[ ] =25 и дисперсией D[ ] =100. Напишите выражение для плотности вероятности f(x) и функции распределения F(x). Чему равна вероятность события 15£ £35?

12. Производится измерение вала без систематических ошибок. Случайные ошибки измерения подчинены нормальному закону распределения со средним квадратическим отклонением, равным 1 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 1 мм.

13. Случайная величина , сосредоточенная на интервале [2;6], задана функцией распределения F(x)=1/16(x²–4x+4). Найти вероятность того, что случайная величина примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.

14. Все значения равномерно распределенной случайной величины принадлежат отрезку [3; 9]. Найти вероятность попадания значения случайной величины : а) в отрезок [1; 5]; б) в отрезок [4; 10 ].

15. Автоматический станок производит однотипные изделия, номинальный размер которых равен 3 см. Фактический размер изделий имеет разброс, подчиненный нормальному закону с s[ ] =0,05 см. Систематические отклонения размера отсутствуют. При контроле отбраковываются все изделия, размер которых отличается от номинального больше, чем на 0,12 см. Определить, какой процент изделий в среднем будет отбраковываться.

16. Завод изготовляет шарики для подшипников, номинальный диаметр которых равен 10 мм, а фактический диаметр случаен и распределен по нормальному закону с математическим ожиданием, равным 10 мм и средним квадратическим отклонением 0,4 мм. При контроле бракуются все шарики, не проходящие через круглое отверстие диаметром 10,7 мм, и все, проходящие через круглое отверстие диаметром 9,3 мм. Какой процент шариков в среднем будет отбраковываться?

17. Случайная величина – ошибка измерительного прибора распределена по нормальному закону с дисперсией, равной 16 мкм и математическим ожиданием, равным нулю. Найти вероятность того, что величина ошибки при одном измерении не превзойдет по абсолютной величине 6 мкм.

18. Измерительный прибор имеет систематическую ошибку, равную 5 м и среднее квадратическое отклонение случайной ошибки – 75 м. (Предполагается, что возникающие ошибки распределены по нормальному закону.) Какова вероятность того, что ошибка измерения не превзойдет по абсолютной величине 5 м?

19. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением, равным 100 м. Найти вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м.

20. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением, равным 100 м. Найти вероятность того, что измеренная дальность не превзойдет истинной.

21. Коробки с шоколадом упаковываются автоматически: их средняя масса равна 1,06 кг. Найти среднее квадратическое отклонение, если известно, что 5% коробок имеют массу, меньшую 1 кг. Предполагается, что масса коробок распределена по нормальному закону.

22. Размер деталей подчинен закону нормального распределения с математическим ожиданием 15 мм и дисперсией 0,25 мм². Определить ожидаемый процент брака, если допустимые размеры деталей находятся в пределах от 14 до17 мм.

23. Найти среднее время безотказной работы устройства, если известно, что для данного устройства вероятность работы без сбоев в течение 100 часов равна 0,2. (Предполагается, что время безотказной работы распределено по экспоненциальному закону.)

24. Считается, что изделие – высшего качества, если отклонение его размеров от номинальных не превосходит по абсолютной величине 3,6 мм. Случайные отклонения размера изделия от номинального подчиняются нормальному закону со средним квадратичным отклонением, равным 3 мм. Систематические отклонения отсутствуют. Определить среднее число изделий высшего качества среди 100 изготовленных.

25. Время безотказной работы механизма подчинено показательному закону с плотностью распределения вероятностей 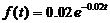при t >0 (t – время в часах). Найти вероятность того, что механизм проработает безотказно 100 часов.

26. Считается, что отклонение длины изготавливаемых деталей от стандартной является случайной величиной, распределенной по нормальному закону. Систематические отклонения размера детали от номинала отсутствуют. Зная, что длина стандартной детали 40 см, а среднее квадратичное отклонение равно 0,4 см, определить, какую точность длины изделия можно гарантировать с вероятностью 0,8.

27. Случайная ошибка измерения дальности импульсным радиодальнометром имеет нормальное распределение со средним квадратическим отклонением, равным 50 м. Найти вероятность того, что измеренное значение дальности будет отличаться по абсолютной величине от истинного не более чем на 30 м, если систематическая ошибка дальнометра равна +20 м.

28. Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,04А.

29. Валик, изготовленный автоматом, считается стандартным, если отклонение его диаметра от проектного размера не превышает 2 мм. Случайные отклонения диаметра валиков подчиняются нормальному закону со средним квадратичным отклонением 1,6 мм и математическим ожиданием, равным 0. Сколько стандартных валиков (в %) изготовляет автомат?

30. Предполагая, что время, необходимое для ремонта поступившего вагона, распределено по экспоненциальному закону с параметром l =0,25[час^-1], найти вероятность того, что для ремонта одного вагона понадобится не более шести часов.

Date: 2015-07-23; view: 2812; Нарушение авторских прав