
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача 3. Завод в среднем дает 27% продукции высшего качества и 70% первого сорта. Найти вероятность того, что наудачу взятое изделие будет или высшего качества или первого сорта
Решение: Обозначим интересующее нас событие буквой С – наудачу взятое изделие будет высшего качества или первого сорта. Рассмотрим вспомогательные события, вероятности которых заданы в условии задачи. Пусть событие А – взятое изделие высшего качества, тогда Р(А)= 0,27; событие В – взятое изделие первого сорта, тогда Р(В)= 0,7. Событие С=А+В, причем А и В – несовместные события. Вероятность события С можно подсчитать по формуле (3) сложения вероятностей двух несовместных событий Р(С)=Р(А+В)=Р(А)+Р(В). Итак, Р(С)= 0,27+0,7=0,97.
Задача 4. Рабочий обслуживает два станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,8, а для второго 0,7. Вычислить вероятность того, что хотя бы один из двух станков не потребует внимания рабочего в течении часа.
Решение: Обозначаем интересующее нас событие, состоящее в том, что хотя бы один из станков не потребует внимания рабочего в течение часа, буквой С. Событие С означает, что либо первый станок не потребует внимания рабочего (событие А), либо второй станок не потребует внимания рабочего (событие В), возможно, что оба станка одновременно не потребуют внимания рабочего. Следовательно, событие С=А+В, причем А и В – совместные события. Для определения вероятности события С используем формулу (4) сложения вероятностей двух совместных событий: Р(С)=Р(А+В)=Р(А)+Р(В) –Р(АВ). По условию Р(А)= 0,8, Р(В)= 0,7. Событие А и В – независимые, поэтому Р(АВ)=Р(А)Р(В) – формула вероятности произведения двух независимых событий. Таким образом, Р(С)= 0,8+0,7-0,8•0,7=0,94.
Задача 5. Студент пришел на экзамен, зная лишь 20 вопросов из 25 вопросов программы. Экзаменатор задал студенту наугад 2 вопроса. Найти вероятность того, что студент знает оба вопроса.
Решение: Введем обозначения событий: А – студент знает первый вопрос;
В – студент знает второй вопрос. Вероятность того, что студент знает первый вопрос можно подсчитать используя формулу (1) классического определения вероятности события, в которой п = 25 – общее число вопросов, m= 20 - число вопросов, ответы на которые студент знает. Р (А) = 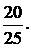 По той же формуле (1) можно подсчитать условную вероятность того, что студент знает ответ на второй вопрос при условии, что он ответил правильно на первый вопрос. Но n = 24, так как студент ответил на первый вопрос и он не присутствует среди предложенных; m = 19, так как на один, известный студенту вопрос, он представил правильный ответ.
По той же формуле (1) можно подсчитать условную вероятность того, что студент знает ответ на второй вопрос при условии, что он ответил правильно на первый вопрос. Но n = 24, так как студент ответил на первый вопрос и он не присутствует среди предложенных; m = 19, так как на один, известный студенту вопрос, он представил правильный ответ.
P(B/A) = 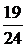 . Вероятность же интересующего нас события подсчитаем по формуле (5): Р(А·В) = P(A)·P(A/B). Итак, Р (АВ) =
. Вероятность же интересующего нас события подсчитаем по формуле (5): Р(А·В) = P(A)·P(A/B). Итак, Р (АВ) = 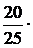
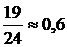 .
.
Задача 6. В некоторой отрасли 25% продукции производится предприятием I, 30% продукции – предприятием II, а остальная часть продукции – предприятием III. На предприятии I в брак идет 1% продукции, на предприятии II – 2% продукции, а на предприятии III – 1,5%. Найти вероятность того, что купленная единица продукции оказалась браком. Какова вероятность того, что она произведена предприятием I?
Решение: Обозначим событие: А – купленная единица продукции оказалась браком. Рассмотрим гипотезы: Н1 – изделие произведено предприятием I; Н2 – изделие произведено предприятием II, Н3 – изделие произведено предприятием III. Тогда вероятность Р (Н1) = 0,25; Р (Н2) = 0,30; Р (Н3) = 1- (0,25 + 0,30) = 0,45. Последняя вероятность подсчитана из условия: Р (Н1)+ Р (Н2)+ Р (Н3) = = 1, так как Н1, Н2, Н3 образуют полную группу несовместных событий.
Условные вероятности события А при этих гипотезах соответственно равны: Р (А/Н1) = 0,01; Р (А/Н2) = 0,02; Р (А/Н3) = 0,015. Используем формулу полной вероятности: Р (А) = Р (Н1) Р (А/Н1) + Р (Н2) Р (А/Н2)+ Р (Н3) Р (А/Н3), тогда Р(А)= 0,25·0,01 + 0,30·0,02 + 0,45·0,015 = 0,01525 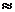 0,015.
0,015.
Вероятность того, что купленная единица произведена предприятием I, найдем по формуле Байеса:
Р (Н1/A) = 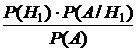 , тогда Р (Н1/A)=
, тогда Р (Н1/A)= 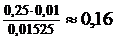
Таким образом, из всех бракованных изделий отрасли в среднем 16% выпускается предприятием I.
3. Схема Бернулли повторных независимых испытаний
Если произведена серия из п независимых испытаний, результатом каждого из которых является появление события А или противоположного ему события Ā, причем вероятность появления события А в каждом испытании одна и таже, и равна р, а Р (Ā) = 1 –р = q, то имеет место схема Бернулли.
Формула Бернулли:
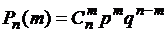 , ,
| (8) |
где m= 0,1,2,..., n определяет вероятность того, что в n испытаниях Бернулли событие А появится m раз.
Задача 7. Машина – экзаменатор содержит 10 вопросов, на каждые из которых предлагается 4 варианта ответов. Положительная оценка ставится машиной в том случае, когда экзаменующийся отвечает правильно не менее, чем на 7 вопросов. Какова вероятность ответить правильно на 5 вопросов? Какова вероятность получения положительной оценки, выбирая ответ наудачу?
Решение: Всего вопросов n= 10. Вероятность ответить на вопрос правильно p= 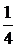 , так как на каждый вопрос предлагается 4 варианта ответов, среди которых один правильный. Вероятность ответить правильно на 5 вопросов из данных 10 можно подсчитать на формуле Бернулли (10), так как имеем дело со схемой Бернулли. n= 10, т= 5, p=
, так как на каждый вопрос предлагается 4 варианта ответов, среди которых один правильный. Вероятность ответить правильно на 5 вопросов из данных 10 можно подсчитать на формуле Бернулли (10), так как имеем дело со схемой Бернулли. n= 10, т= 5, p= 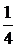 , q= 1– р, то есть q=
, q= 1– р, то есть q= 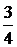 ,
,
Р10 (5) = 
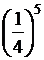
 =
= 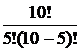
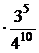 =
= 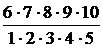
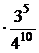 ≈ 0,0584.
≈ 0,0584.
Обозначим через В событие, состоящее в получении положительной оценки, тогда В=В7+В8+В9+В10= 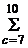 Вi, где событие Вi – экзаменующийся ответит правильно на i вопросов. Вероятность события В.
Вi, где событие Вi – экзаменующийся ответит правильно на i вопросов. Вероятность события В.
Р(В)=Р(В7)+Р(В8)+Р(В9)+Р(В10)=С710 р7 q3+С810 р8 q2+ С910 р9 q1+ С1010 р10 q0 =  (
(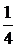 )7(
)7(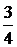 )3+
)3+ 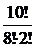 (
(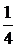 )8(
)8(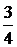 )2+
)2+ 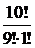 (
(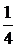 )9(
)9(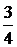 )1+
)1+  (
(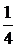 )10(
)10(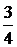 )0=
)0= 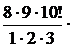
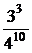 +
+ 
 +
+ 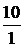
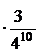 +
+ 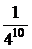 =
= 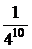 (4·10·34+5·34+10·3+1) ≈0,0035.
(4·10·34+5·34+10·3+1) ≈0,0035.
Date: 2015-07-22; view: 6549; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |