
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгоритм решения задач по теме
1.
|
|
|
|
|




 Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости α, а катет наклонен к этой плоскости под углом 30º. Найдите угол между плоскостью α и плоскостью треугольника.
Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости α, а катет наклонен к этой плоскости под углом 30º. Найдите угол между плоскостью α и плоскостью треугольника.
 |
Дано:
Δ АВС; ∠ С = 90 º;
Угол между ВС и α = 30 º
Найти двугранный угол с ребром АВ.
Решение:
1. Строим линейный угол двугранного угла с ребром АВ.
СО  α; CD – наклонная к плоскости α;
α; CD – наклонная к плоскости α;
OD  АВ (по построению);
АВ (по построению);
СВ 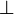 АВ (по теореме о трех перпендикулярах. Следовательно ∠СDО – линейный угол двугранного угла с ребром АВ).
АВ (по теореме о трех перпендикулярах. Следовательно ∠СDО – линейный угол двугранного угла с ребром АВ).
∠ СВО – угол наклона ВС к плоскости α.
Пусть СО = α;
1.
|
|
|
|
|
|
|
|
|
|
|
|




 2.
2.
Рассмотрим ΔСОВ: ∠В=30 º; СВ = 2а (свойство катета, лежащего против угла в 30 º).
Рассмотрим ΔACD: SΔ = 0,5*АС*СВ = 0,5*2а*2а=2а2
SΔ = 0,5*АВ*СD;CD=2* SΔ/АВ
АВ =√АС2+СВ2 = √4а2+4а2 = √8а2 = 2а√2
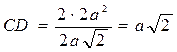 ;
;

3. 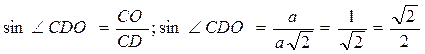 ;
;
Ответ: ∠CDO=45º
2.
|
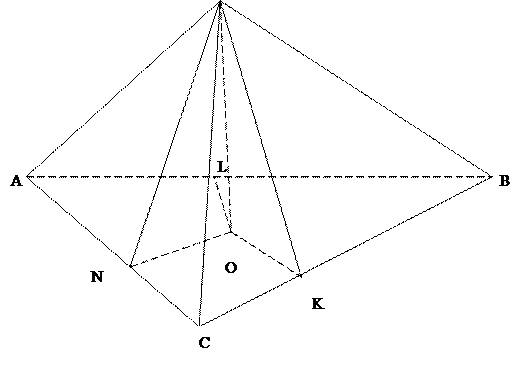 |
Дано:
Δ АВС;
АВ=АС=ВС=4см;
МО=2 см.
Найти: 1. Угол между (ВМС) и (АВС)
2.Угол между МС и (АВС)
Решение:
Так как точка М равноудалена от всех сторон треугольник АВС, то ее проекцией на плоскость (АВС) является центр вписанной окружности, следует ОК=ON = OL =r;
ОК  ВС (радиус, проведенный в точку касания); ОМ
ВС (радиус, проведенный в точку касания); ОМ  (АВС);
(АВС);
МК – наклонная к (АВС);
ОК = пр. (АВС) МК; ОК  ВС следует, что МК
ВС следует, что МК  ВС следует,что ∠ МКО – линейный угол двугранного угла МСВО.
ВС следует,что ∠ МКО – линейный угол двугранного угла МСВО.
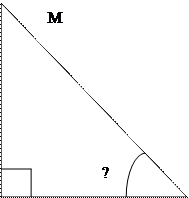
2)Рассмотрим Δ МОК;
 | |||||
| |||||
| |||||
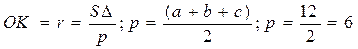
 ;
; 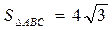
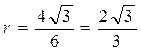 ;
;
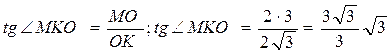
∠ МКО= 60º
3) Угол между МС и плоскостью (АВС) равен углу МСО.
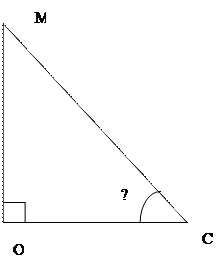 |
ОС=R; R=2r; 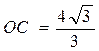
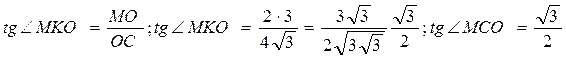
Ответ: ∠ МКО= 60º; 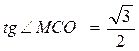
Варианты заданий для самостоятельной работы
Вариант № 1
1) Дан прямоугольник АВСD и точка S не лежит в его плоскости. Построить линейный угол двугранного угла с ребром DC, если:
SB 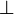 (АВС)
(АВС)
О – точка пересечения диагоналей, SO 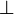 (АВС).
(АВС).
2) Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ1. Найдите расстояние от точки В до прямой АС и до плоскости α, если АВ =2 см.; ∠ ВАС = 150º; и двугранный угол ВАСВ1 = 45 º.
Вариант № 2
1) ABCD - ромб; BD=8см; двугранный угол с ребром BD = 45º. Найти площадь ромба.
2) В параллелограмме ABCD ∠АDC=150º; АD=16см; DC=12см; SC 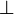 (АВС); SC=18см. Найти величину двугранного угла с ребром AD и площадь параллелограмма.
(АВС); SC=18см. Найти величину двугранного угла с ребром AD и площадь параллелограмма.
Вариант № 3
1) Дан куб ABCDА1В1С1D1; (ABCD – нижнее основание). Найдите величину угла между плоскостью грани АВВ1А1 куба и плоскостью, проходящего через диагональ АВ1 этой грани и середину ребра DC куба.
2) Плоскость α проходит через сторону АС треугольника АВС под углом 30º к плоскости треугольника. Найти расстояние от вершины В до плоскости α, если ВС = 6 см; ∠С=120º.
Вариант № 4
1) В тетраэдре DABC все ребра, кроме АВ, имеют равные длины. ∠АСВ=90º. Найдите величину двугранного угла при ребре ВС.
2) Через сторону AD ромба ABCD проведена плоскость ADM так, что двугранный угол BACD =90º. Найдите сторону ромба, если ∠BAD=45º и расстояние от точки В до плоскости ADM = 4√3см.
Вариант № 5
1) Найти величину двугранного угла с ребром АС, если:
а) BS 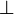 (ABC); ∠ C=90º; BC= BS=6см.
(ABC); ∠ C=90º; BC= BS=6см.
б) BS 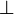 (ABC); АВ=ВС=10см; BS=АС=12см.
(ABC); АВ=ВС=10см; BS=АС=12см.
2) ABCD – прямоугольник. S=48см2 ; DC=4см; OS 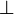 (АВС); OS=6см. найти величину двугранного угла с ребром DC.
(АВС); OS=6см. найти величину двугранного угла с ребром DC.
Вариант № 6
1) Дан прямоугольник ABCDи точка S не лежит в его плоскости. Построить линейный угол двугранного угла с ребром DC если: SB 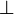 (АВС); О – точка пересечения диагоналей, прямая SO
(АВС); О – точка пересечения диагоналей, прямая SO 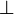 (АВС).
(АВС).
2) Точка М равноудалена от всех сторон правильного треугольника АВС, сторона которого 4см. Расстояние от точки М до плоскости (АВС) равно 2 см. Найдите угол между плоскостью (ВМС) и плоскостью (АВС) и угол между МС и плоскостью (АВС).
6. Решение стереометрических задач на тему «Двугранный угол»
1) Грань ABCD прямоугольного параллелепипеда ABCD A1B1C1D1 является квадратом со стороной 3, а пространственная диагональ параллелепипеда равна 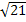 . Найдите угол между плоскостью A1B1C1D1 и плоскостью ADC1
. Найдите угол между плоскостью A1B1C1D1 и плоскостью ADC1
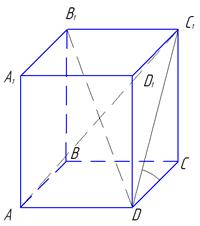
Дано: 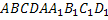 - прямоугольный параллелепипед
- прямоугольный параллелепипед
ABCD – квадрат
AB=3
B1D= 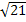
Найти угол между плоскостями (A1B1C1D1) и (ADC1)
Решение
Двугранный угол С1ADC. Строим его линейный угол. 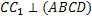 ;
; 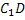 - наклонная к плоскости
- наклонная к плоскости 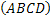 ;
; 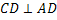 (стороны квадрата) по теореме, обратной теореме о трёх перпендикулярах
(стороны квадрата) по теореме, обратной теореме о трёх перпендикулярах 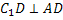 , значит
, значит 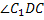 - линейный угол двугранного угла
- линейный угол двугранного угла 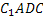 .
.
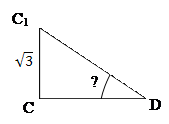 |


|
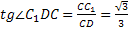 ;
; 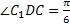
|


|
|
|
|

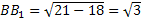
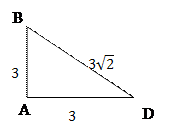 |
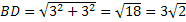
Ответ: 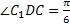
2) Диаметр и хорда AB основания конуса равны соответственно 26 и 24, тангенс угла между образующей и основанием конуса равен 8. Найдите тангенс угла между плоскостью основания конуса и плоскостью сечения конуса, проходящей через вершину конуса и хорду AB.
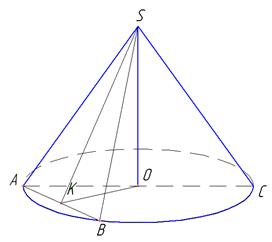 Дано: SAC – конус
Дано: SAC – конус
AC=26
AB=24

Найти: 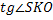
Решение
|

 Строим линейный угол двугранного угла SABO.
Строим линейный угол двугранного угла SABO.
1)
 | |||
 | |||
|
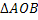 – равнобедренный.
– равнобедренный.
| |||
 | |||
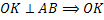 - медиана на
- медиана на 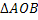 .
.
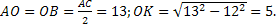
|
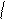
|
|
 2)
2)
|
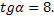
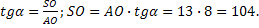
|
|
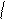
|
 3)
3)
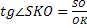 ;
;
|
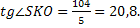
Ответ: 
3) Основание прямой призмы ABCDA1B1C1D1 – ромб ABCD со стороной, равной 7. Площадь ромба равна 28. Тангенс угла между плоскостью основания призмы и плоскостью ABC1 равен 2,75. Найдите длину бокового ребра призмы.

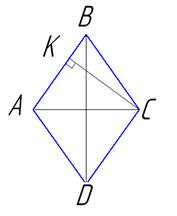
Дано: ABCDA1B1C1D1 – прямоугольная призма
ABCD – ромб.
AB=7.
S ромба=28.
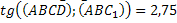
Найти: DD1
Решение
1) Проведём 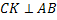 тогда
тогда 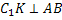 (по теореме о трёх перпендикулярах), тогда
(по теореме о трёх перпендикулярах), тогда 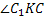 - линейный угол двухгранного угла C1ABC.
- линейный угол двухгранного угла C1ABC.
2) 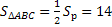
|
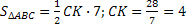
3)
 |
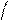

|
|
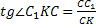

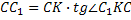
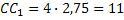
Ответ: 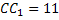 .
.
4) Высота прямой призмы ABCA1B1C1 с основанием ABC равна 12. Угол между прямыми BC1 и AC равен 90º, а синус угла между прямыми A1B и AC равен 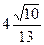 . Найдите тангенс угла между плоскостью BC1A и плоскостью ABC, если A1B равно 13.
. Найдите тангенс угла между плоскостью BC1A и плоскостью ABC, если A1B равно 13.
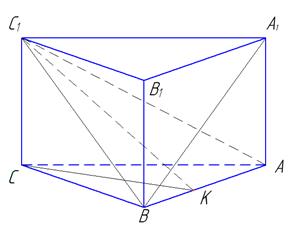 Дано:
Дано:
ABCA1B1C1 – прямая призма
АА1=12
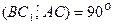
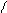
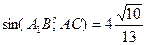
Найти: 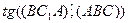
Решение
Прямые DC1 и AC – скрещивающиеся. 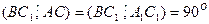
Прямые A1B и AC – скрещивающиеся.
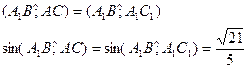
Двугранный угол C1ABC. Строим его линейный угол.
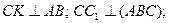
C1K – наклонная; 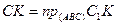
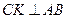 (по построению)
(по построению) 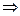 по теореме о трёх перпендикулярах
по теореме о трёх перпендикулярах 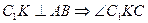 - линейный угол двугранного угла
- линейный угол двугранного угла 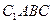 .
.
|
|


|
|
|
 1)
1) 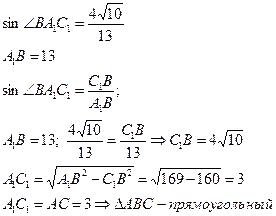
2)
|





|
|
|
|
|

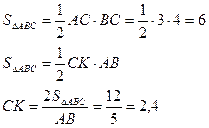
|
 3)
3)
|
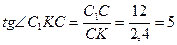
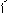 | |||||
 | |||||
| |||||
Ответ: 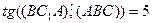
Date: 2015-07-10; view: 6506; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |
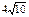 1
1