
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

подследовательности. Частные пределы
Пусть имеем последовательность 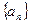 . Возьмем некоторую монотонно возрастающую последовательность натуральных чисел:
. Возьмем некоторую монотонно возрастающую последовательность натуральных чисел: 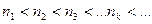 и рассмотрим члены последовательности
и рассмотрим члены последовательности 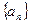 с индексами
с индексами 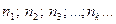 , т.е.
, т.е. 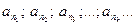 . Полученная новая последовательность называется подпоследовательностью последовательности
. Полученная новая последовательность называется подпоследовательностью последовательности 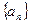 и обозначают
и обозначают 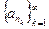
Например, все члены последовательности 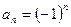 при четных номерах равны 1, а при нечетных равны –1.
при четных номерах равны 1, а при нечетных равны –1.
Определение. Если подпоследовательность 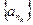 последовательности
последовательности 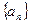 имеет предел, то данный предел называется частным пределом последовательности
имеет предел, то данный предел называется частным пределом последовательности 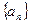 .
.
Последовательность может не иметь предел, но иметь частные пределы.
Например,
1) 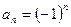 ; при
; при 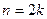
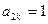 (частный предел 1); при
(частный предел 1); при 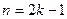
 (частный предел –1).
(частный предел –1).
2) 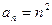 не имеет конечных частных пределов.
не имеет конечных частных пределов.
Теорема1. Если последовательность сходится (т.е. имеет предел), то любая ее подпоследовательность тоже сходится и сходится к тому же числу, что и сама последовательность, т.е. если 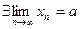 , то
, то 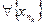
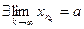 .
.
Доказательство: Рассмотрим произвольную подпоследовательность 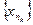 последовательности
последовательности 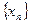 и докажем, что она сходится и сходится к числу
и докажем, что она сходится и сходится к числу 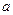 .
.
 . Т.к. последовательность
. Т.к. последовательность 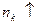 и
и 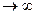 , то
, то 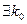 , что
, что 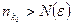 . Тогда
. Тогда 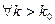 ,
, 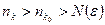
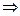
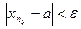 . Ч.т.д.
. Ч.т.д.
Следовательно, сходящаяся последовательность имеет один единственный частный предел – предел последовательности.
Теорема2. Если любая подпоследовательность 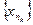 последовательности
последовательности 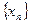 сходится и сходится к одному и тому же числу
сходится и сходится к одному и тому же числу 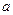 , то и сама последовательность сходится и сходится к числу
, то и сама последовательность сходится и сходится к числу 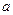 .
.
Доказательство очевидно, т.к. сама последовательность для себя является подпоследовательностью.
Теорема3. Последовательность 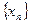 сходится тогда и только тогда, когда любая подпоследовательность данной последовательности сходится, и сходится к одному и тому же пределу.
сходится тогда и только тогда, когда любая подпоследовательность данной последовательности сходится, и сходится к одному и тому же пределу.
Доказательство: Пусть имеем последовательность 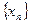 и обозначим через
и обозначим через 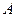 множество всех частных пределов. Из теоремы 1 и теоремы 2 следует, что если последовательность сходится, то множество
множество всех частных пределов. Из теоремы 1 и теоремы 2 следует, что если последовательность сходится, то множество 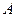 состоит из одной точки – это предел последовательности, а также если содержит более одной точки, то
состоит из одной точки – это предел последовательности, а также если содержит более одной точки, то 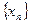 – рассходится. Т.е. если
– рассходится. Т.е. если  , то
, то 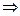 что
что  .
.
Например, если
а) 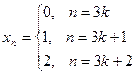 , то
, то 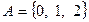 ;
;
б) 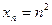 , то
, то 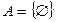 , т.к. в этом случае
, т.к. в этом случае 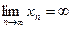 (т.е нет конечных частных пределов).
(т.е нет конечных частных пределов).
Следовательно, последовательность 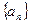 не сходится если: не имеет частных конечных пределов или имеет более одного конечного предела. Для этого следует рассматривать только ограниченные последовательности. Оказывается, для ограниченных последовательностей всегда существует конечный частный предел, т.е имеет место следующая теорема.
не сходится если: не имеет частных конечных пределов или имеет более одного конечного предела. Для этого следует рассматривать только ограниченные последовательности. Оказывается, для ограниченных последовательностей всегда существует конечный частный предел, т.е имеет место следующая теорема.
Теорема Больцано-Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, т.е. любая ограниченная последовательность имеет частный предел.
Доказательство: пусть имеем ограниченную последовательность 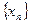 , т.е.
, т.е. 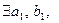 что
что  . Разделим отрезок пополам и рассмотрим два отрезка
. Разделим отрезок пополам и рассмотрим два отрезка  и
и 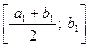 .
.
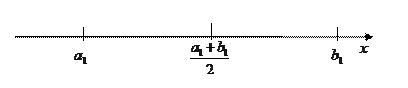
Как минимум в одном из данных отрезков находится бесконечное множество членов последовательности 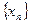 . Действительно, если это не так, то в обоих отрезках существуют конечные члены данной последовательности. Допустим, что в первом отрезке существуют
. Действительно, если это не так, то в обоих отрезках существуют конечные члены данной последовательности. Допустим, что в первом отрезке существуют 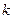 членов, а во втором
членов, а во втором 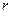 членов, следовательно, в обоих отрезках существуют
членов, следовательно, в обоих отрезках существуют 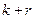 членов, откуда следует, что последовательность состоит из
членов, откуда следует, что последовательность состоит из 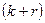 членов, а ведь последовательность
членов, а ведь последовательность 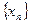 состоит из бесконечного числа элементов. Пришли к противоречию. Обозначим через
состоит из бесконечного числа элементов. Пришли к противоречию. Обозначим через  данный отрезок (т.е. либо первый отрезок либо второй, т.е тот отрезок где находится бесконечное множество членов последовательности). Разделим его пополам. Опять, как минимум в одном из данных отрезков будут существовать бесконечное множество членов последовательности
данный отрезок (т.е. либо первый отрезок либо второй, т.е тот отрезок где находится бесконечное множество членов последовательности). Разделим его пополам. Опять, как минимум в одном из данных отрезков будут существовать бесконечное множество членов последовательности 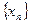 . Обозначим данный отрезок через
. Обозначим данный отрезок через  и продолжим этот процесс до бесконечности. И тем самым получим, что
и продолжим этот процесс до бесконечности. И тем самым получим, что  содержит в себе
содержит в себе  , а этот отрезок содержит –
, а этот отрезок содержит –  , и т.д., а из построения следует, что
, и т.д., а из построения следует, что 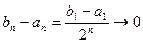 . Следовательно, выполняются все условия теоремы о вложенных отрезках: существует, и притом единственная точка
. Следовательно, выполняются все условия теоремы о вложенных отрезках: существует, и притом единственная точка 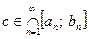 .
.
Построим подпоследовательность последовательности 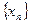 следующим образом: возьмем отрезки
следующим образом: возьмем отрезки  ,
,  ,...,
,..., 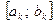 и рассмотрим
и рассмотрим 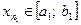 ,
,  ,...,
,..., 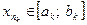 , где
, где 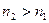 ,...,
,..., 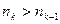 . Получим последовательность
. Получим последовательность 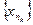 , где
, где 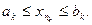 Возьмем точку
Возьмем точку 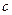 ,
, 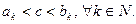 Тогда, можно сказать, что
Тогда, можно сказать, что 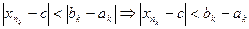 , а т.к.
, а т.к.  , то
, то 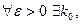 если
если 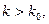 то
то 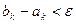 , для
, для  Следовательно,
Следовательно, 
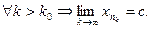
Date: 2015-07-02; view: 653; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |