Многочлены

I Общие результаты

Определение 1. Многочленом 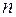-ой степени называют функцию вида

,

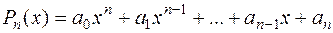где 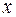– переменная (вообще говоря, комплексная), – некоторые постоянные числа (вообще говоря, комплексные), причём .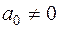

Известно, что многочлены можно делить «столбиком» и справедлива теорема.

Теорема 1. Каковы бы ни были многочлены 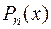и 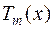, , 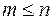найдутся многочлены 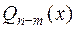и 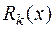, причем 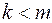, такие, что имеет место равенство:

.

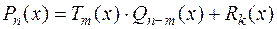По отношению к четырём многочленам из этой теоремы применяют обычные термины: делимое, делитель, частное, остаток.

Говорят, что 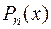делится на 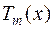, если остаток .

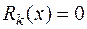Многочленом нулевой степени естественно называть любое постоянное число (вещественное или комплексное).

Определение 2. Число 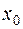называют корнем многочлена 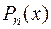, если .

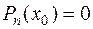Теорема 2 (Безу). Остаток от деления 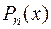на бином 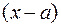есть значение многочлена в точке .

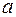Действительно, т.к. делитель 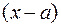имеет первую степень, то остаток должен быть нулевой степени:

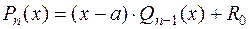
Тогда 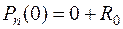, что и требовалось доказать.

Из этой теоремы вытекает важное следствие (которое часто называют теоремой Безу).

Следствие. Число 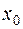является корнем многочлена 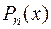тогда и только тогда, когда 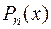делится на 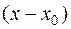, т.е.

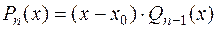
Заметим, что старший коэффициент частного совпадает со старшим коэффициентом делимого .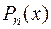

Ответ на вопрос о наличии корней у многочлена даёт основная теорема алгебры, которую принимаем без доказательства.

Теорема 3. Всякий многочлен ненулевой степени имеет, по крайней мере, один корень (вещественный или комплексный).

Из этой теоремы можно получить ряд следствий.

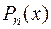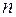1. Всякий многочлен , можно разложить на линейных множителей

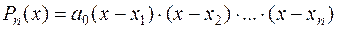. (1)

2. Многочлен степени 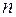имеет не более чем 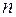различных корней.

Из разложения (1) следует, что числа 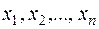– корни многочлена 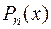и других чисел, обращающих многочлен в нуль, нет.

3. В разложении (1) множители могут повторяться; если через 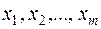обозначить различные корни многочлена 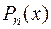получим:

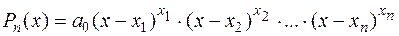, (2)

Здесь 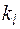называют кратностью корня 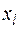и 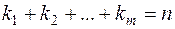. Можно дать такое определение кратности корня: число 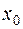называют 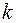-кратным корнем многочлена 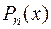, если

и .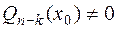

4. Всякий многочлен степени 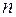() имеет ровно 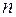корней, если каждый

из корней считать столько раз, какова его кратность.

II Многочлены с действиьтельными коэффициентами

Пусть комплексное число 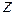является корнем многочлена с действительными коэффициентами, т.е. 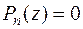и 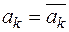, 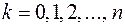. Рассмотрим число 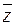и вспомним, что операция “сопряжения” перестановочна с любой арифметической операцией. Тогда:

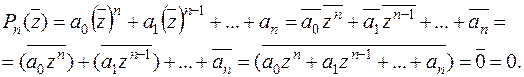
Итак, справедлива теорема.

Теорема 4. Если комплексное число 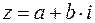является корнем многочлена с действительными коэффициентами, то и сопряжённое ему число 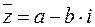является корнем этого многочлена (причём, с той же кратностью).

Из этой теоремы можно получить ряд следствий.

1. У многочлена с действительными коэффициентами число комплексных корней – чётно.

2. Многочлен нечётной степени (с действительными коэффициентами) имеет, по крайней мере, один действительный корень.

3. В разложении (2) перемножим скобки, соответствующие комплексным сопряжённым корням:

,

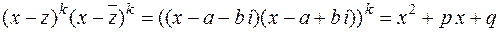где 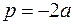, 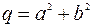. Таким образом, получим основной результат:

всякий многочлен с действительными коэффициентами можно разложить в произведение множителей двух типов: линейных – 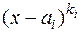и квадратичных – 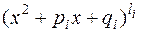, где 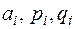– действительные числа, причём 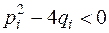. Линейные множители соответствуют действительным корням, квадратичные – парам комплексных сопряжённых.

Список рекомендованной литературы

1. Ильин В.А., Позняк Э.К. Основы математического анализа, ч. I. – М.: «Наука», 1982. – с. 616.

2. Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: «Наука», 1966. – с. 544.

3. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). – М.: «Высш. школа», 1983. – с. 175.

4. Методические указания и задания к расчетно-графической работе по разделу курса высшей математики «Пределы, непрерывность, производная» (для студентов направления подготовки 6.050102 «Программная инженерия»)/ Составитель: Скворцов А.Е.– Донецк: ДонНТУ, 2008. – с. 48

Date: 2015-07-02; view: 593; Нарушение авторских прав