Геометрия

10-11

*****

ГЕОМЕТРИЯ 10

Введение

2.

n Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

● Аксиома 2. Если две точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости.

● Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все их общие точки.

3.

n Теорема. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

n Теорема. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

ГЛАВА 1

Параллельность прямых и плоскостей

§ 1. Параллельность прямых, прямой и плоскости.

4.

n Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

n Теорема (о параллельных прямых). Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

 Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.

5.

● Лемма (о пересечении параллельными прямыми плоскости). Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

n Теорема (о связке параллельных прямых). Если две прямые параллельны третьей, то они параллельны.

6.

n Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

● Теорема (признак параллельности прямой и плоскости). Если прямая, не лежащая в плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскость.

○ Замечание 1. Если прямая параллельна плоскости и лежит в плоскости, пересекающей данную, то прямая параллельна линии пересечения плоскостей.

○ Замечание 2. Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо также параллельна этой плоскости, либо лежит в ней.

§ 2. Взаимное расположение прямых в пространстве. Угол между двумя прямыми.

7.

 Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

● Теорема (признак скрещивающихся прямых). Если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.

○ Следствие. Возможны три случая взаимного расположения двух прямых в пространстве:

а) прямые пересекаются;

б) прямые параллельны;

в) прямые скрещиваются.

n Теорема (свойство скрещивающихся прямых). Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

8.

○ Определение. Полуплоскостью называется каждая из двух частей, на которые прямая, лежащая в плоскости, делит эту плоскость.

○ Определение. Два луча называются сонаправленными, если

1) они параллельны и лежат в одной полуплоскости с границей, проходящей через их начала, или

2) они лежат на одной прямой и совпадают или один из них содержит другой.

● Теорема (об углах с сонаправленными сторонами). Углы с сонаправленными сторонами равны.

9.

○ Определение. Углом между пересекающимися прямыми называется наименьший из углов, образованных ими.

○ Определение. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными данным.

○ Теорема (корректность определения скрещивающихся прямых). Угол между скрещивающимися прямыми не зависит от выбора пересекающихся прямых, им параллельных.

§ 3. Параллельность плоскостей.

10.

● Определение. Две плоскости называются параллельными, если они не имеют общих точек.

n Теорема (признак параллельности плоскостей). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

11.

 Теорема (1 свойство параллельных плоскостей). Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

 Теорема (2 свойство параллельных плоскостей). Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

○ Теорема (3 свойство параллельных плоскостей (N 55)). Если прямая пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость.

○ Теорема (4 свойство параллельных плоскостей (N 58)). Если плоскость пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость.

○ Теорема (5 свойство параллельных плоскостей (N 59)). Через любую точку пространства, не лежащую в данной плоскости, проходит плоскость, параллельная данной, и притом только одна.

○ Теорема (2 признак параллельности плоскостей (N 60)). Если две плоскости параллельны третьей, то они параллельны.

§ 3. Тетраэдр и параллелепипед.

12.

○ Определение. Два ребра тетраэдра называются противоположными, если они не имеют общих вершин.

13.

○ Определение. Две грани параллелепипеда называются противоположными, если они не имеют общих ребер.

○ Определение. Две грани параллелепипеда называются смежными, если они имеют общее ребро.

○ Определение. Две вершины параллелепипеда называются противоположными, если они не принадлежат одной грани.

○ Определение. Диагональю параллелепипеда называется отрезок, соединяющий противоположные вершины.

○ Теорема (1 свойство параллелепипеда). Противоположные грани параллелепипеда равны и параллельны.

 Теорема (2 свойство параллелепипеда). Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

14.

 Определение. Секущей плоскостью тетраэдра (параллелепипеда) называется плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллелепипеда).

○ Определение. Сечением тетраэдра (параллелепипеда) называется многоугольник со сторонами, образованными пересечением секущей плоскостью с гранями тетраэдра (параллелепипеда).

ГЛАВА 2

Перпендикулярность прямых и плоскостей

§ 1. Перпендикулярность прямой и плоскости.

15.

○ Определение. Две прямые в пространстве называются перпендикулярными, если угол межу ними равен 90°.

● Лемма (о перпендикулярности двух параллельных прямых к третьей). Если одна из двух параллельных прямых перпендикулярна к третьей, то и другая прямая перпендикулярна к ней.

16.

n Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

 Теорема. Если прямая перпендикулярна к плоскости, то она пересекает эту плоскость.

n Теорема (свойство параллельных прямых). Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

n Теорема(признак параллельных прямых). Если две прямые перпендикулярны к плоскости, то они параллельны.

17.

n Теорема (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

18.

n Теорема (о прямой перпендикулярной к плоскости). Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

○ Теорема (3 признак параллельности плоскостей (N 123)). Если две плоскости перпендикулярны к прямой, то они параллельны.

 Теорема (6 свойство параллельных плоскостей (N 132)). Если одна из двух параллельных плоскостей перпендикулярна к прямой, то и другая плоскость перпендикулярна к этой прямой.

 Теорема (N 133). Через любую точку пространства проходит только одна плоскость перпендикулярная к данной прямой.

 Теорема (N 137). Через каждую из двух взаимно перпендикулярных скрещивающихся прямых проходит плоскость перпендикулярная к другой прямой.

§ 2. Перпендикуляр и наклонные. Угол между прямой и плоскостью.

19.

○ Определение. Перпендикуляром, проведенным из точки к плоскости, называется отрезок, соединяющий данную точку с точкой на плоскости и лежащий на прямой, перпендикулярной плоскости.

○ Определение. Основанием перпендикуляра называется его конец, лежащий на плоскости.

○ Определение. Наклонной, проведенной из точки к плоскости, называется отрезок, соединяющий данную точку с какой-нибудь точкой на плоскости и не являющийся перпендикуляром к этой плоскости.

○ Определение. Основанием наклонной называется ее конец, лежащий на плоскости.

○ Определение. Проекцией наклонной на плоскость называется отрезок, соединяющий основание наклонной с основанием перпендикуляра, проведенного из той же точки к этой плоскости.

 Замечание. Перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.

○ Определение. Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к этой плоскости.

n Замечание 1. Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости.

○ Определение. Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из этих плоскостей до другой плоскости.

n Замечание 2. Если прямая параллельна плоскости, то все точки этой прямой равноудалены от этой плоскости.

○ Определение. Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до этой плоскости.

○ Определение. Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.

20.

n Теорема (о трех перпендикулярах). Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

n Теорема (обратная к теореме о трех перпендикулярах). Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней перпендикулярна и к ее проекции.

21.

 Определение. Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.

○ Определение. Проекцией фигуры F на данную плоскость называется фигура F`, состоящая из проекций всех точек фигуры F на эту плоскость.

○ Теорема. Проекцией наклонной на плоскость является прямая.

○ Следствие. Проекцией отрезка наклонной на плоскость является отрезок.

● Определение. Углом между наклонной и плоскостью называется угол между ней и ее проекцией на эту плоскость.

○ Определение. Угол между перпендикуляром и плоскостью считается равным 90°.

§ 2. Двугранный угол. Перпендикулярность плоскостей.

22.

 Определение. Двугранным углом называется фигура образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.

○ Определение. Гранями двугранного угла называются полуплоскости его образующие.

○ Определение. Ребром двугранного угла называется общая граница его граней.

○ Определение. Линейным углом двугранного угла называется угол, образованный двумя лучами, лежащими в разных его гранях и исходящими из одной точки на его ребре перпендикулярно к ребру.

 Теорема (корректность определения линейного угла двугранного угла). Все линейные углы двугранного угла равны друг другу.

 Определение. Градусной мерой двугранного угла называется градусная мера его линейного угла.

23.

n Определение. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90°.

n Теорема (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

● Следствие. Если плоскость перпендикулярна к прямой, по которой пересекаются две данные плоскости, то она перпендикулярна к каждой из этих плоскостей.

24.

○ Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания являются прямоугольниками.

 Теорема (1 свойство прямоугольного параллелепипеда). В прямоугольном параллелепипеде все шесть граней - прямоугольники.

 Теорема (2 свойство прямоугольного параллелепипеда). Все двугранные углы прямоугольного параллелепипеда - прямые.

■ Теорема (3 свойство прямоугольного параллелепипеда). Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

■ Следствие (4 свойство прямоугольного параллелепипеда). Диагонали прямоугольного параллелепипеда равны.

○ Теорема (о двух плоскостях, перпендикулярных третьей (N 183)). Если две пересекающиеся плоскости перпендикулярны третьей, то их линия пересечения тоже ей перпендикулярна.

○ Теорема (об общем перпендикуляре к скрещивающимся прямым (N 186)). Существует одна и только одна прямая, пересекающая две данные скрещивающиеся прямые и перпендикулярная к каждой из них.

ГЛАВА 3

Многогранники

§ 1. Понятие многогранника. Призма.

25.

○ Определение. Многогранником называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, причем никакие два соседних многоугольника не лежат в одной плоскости.

○ Определение. Гранями многогранника называются многоугольники, из которых составлен многогранник.

○ Определение. Ребрами многогранника называются стороны его граней.

○ Определение. Вершинами многогранника называются концы его ребер.

○ Определение. Диагональю многогранника называется отрезок, соединяющий две вершины, не принадлежащие одной грани.

○ Определение. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости любой его грани.

○ Теорема. В выпуклом многограннике сумма всех плоских углов при его каждой вершине меньше 360°.

27.

○ Определение. n -угольной призмой называется призма, в основании которой лежит n -угольник.

○ Определение. Высотой призмы называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

○ Определение. Призма называется прямой, если ее боковые ребра перпендикулярны к основаниям.

 Замечание. Высота прямой призмы равна ее боковому ребру.

○ Определение. Призма называется наклонной, если ее боковые ребра не перпендикулярны к основаниям.

○ Определение. Призма называется правильной, если она прямая, и ее основания - правильные многоугольники.

○ Замечание. У правильной призмы все боковые грани - равные прямоугольники.

 Определение. Площадью полной поверхности призмы называется сумма площадей всех ее граней.

 Определение. Площадью боковой поверхности призмы называется сумма площадей всех ее боковых граней.

n Теорема (площадь боковой поверхности прямой призмы). Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

 Теорема (N 236)). Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

§ 2. Пирамида.

28.

○ Определение. n -угольной пирамидой называется пирамида, в основании которой лежит n -угольник.

 Замечание. Треугольная пирамида - это тетраэдр.

○ Определение. Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды к плоскости основания.

 Определение. Площадью полной поверхности пирамиды называется сумма площадей всех ее граней.

 Определение. Площадью боковой поверхности пирамиды называется сумма площадей всех ее боковых граней.

29.

 Определение. Пирамида называется правильной, если ее основание - правильный многоугольник, а отрезок соединяющий вершину пирамиды с центром основания, является ее высотой.

○ Замечание 1. У правильной пирамиды все боковые грани - равные равнобедренные треугольники.

○ Замечание 2. У правильной пирамиды все боковые ребра равны.

○ Определение. Апофемой правильной пирамиды называется высота ее боковой грани, проведенная из вершины.

n Теорема (площадь боковой поверхности правильной пирамиды). Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

30.

○ Определение. Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

○ Замечание 1. У усеченной пирамиды все боковые грани - трапеции.

 Определение. Площадью полной поверхности усеченной пирамиды называется сумма площадей всех ее граней.

 Определение. Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней.

 Определение. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

○ Замечание 1. Основания правильной усеченной пирамиды - правильные многоугольники.

○ Замечание 2. Боковые грани правильной усеченной пирамиды - равнобедренные трапеции.

○ Определение. Апофемой правильной усеченной пирамиды называется высота ее боковой грани.

n Теорема (площадь боковой поверхности правильной усеченной пирамиды). Площадь боковой поверхности правильной усеченной пирамиды равна половине произведения полусуммы периметров оснований на апофему.

§ 3. Правильные многогранники.

31.

○ Определение. Точки А и 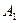называются симметричными относительно точки О (центра симметрии), если О - середина отрезка .

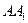○ Замечание. Точка О считается симметричной самой себе.

○ Определение. Точки А и 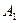называются симметричными относительно прямой а (оси симметрии), если прямая а - серединный перпендикуляр к отрезку .

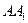○ Замечание. Каждая точка прямой а считается симметричной самой себе.

○ Определение. Точки А и 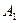называются симметричными относительно плоскости α (плоскости симметрии), если плоскость α проходит через середину отрезка 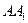и перпендикулярна ему.

○ амечание. Каждая точка плоскости α считается симметричной самой себе.

○ Определение. Точка, (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке этой фигуры.

○ Определение. Элементами симметрии многогранника называются центр, оси и плоскости его симметрии.

32.

 Определение. Выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники и в каждой вершине сходится одно и то же число ребер.

○ Теорема. Не существует правильного многогранника, гранями которого являются правильные n -угольники при n >5.

○ Следствие. Существует 5 видов правильных многогранников:

правильный тетраэдр (состоящий из 4 равносторонних треугольников),

правильный октаэдр (состоящий из 8 равносторонних треугольников),

правильный икосаэдр (состоящий из 20 равносторонних треугольников),

куб (состоящий из 6 квадратов),

правильный додекаэдр (состоящий из 12 правильных пятиугольников).

*****