Правило Лопиталя

Теорема.

Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки x₀, за исключением может быть самой точки x₀, и 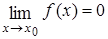, 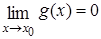. Тогда если существует предел отношения производных функций 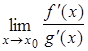, то существует предел отношения самих функций 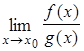, причем они равны между собой, т.е. .

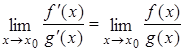Доказательство:

Доопределим f(x) и g(x) в точке x₀, положив

f(x₀) = g(x₀) = 0.

В окрестности точки x₀, т.е. на (x₀,х) для функций f(x) и g(x) выполняются условия теоремы Коши. Следовательно, существует точка сÎ(x₀, х) такая, что

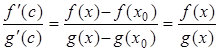, т.к. f(x₀) = g(x₀) = 0.

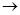Перейдем к пределу при x x₀ с x₀:

.

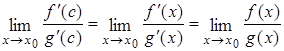Ч.т.д.

Замечание. На практике при раскрытии неопределенности типа 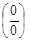можно пользоваться правилом Лопиталя и в случаях, когда x®±¥, x®¥.

Для раскрытия неопределенностей типа 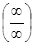существует аналог правила Лопиталя, т.е. справедливо следующее утверждение:

Теорема.

Пусть функции f(x) и g(x) непрерывны и дифференцируемы в некоторой окрестности точки x₀, за исключением самой точки x₀, причем 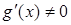. Пусть , 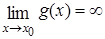. Тогда если существует предел отношения производных функций 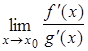, то существует предел отношения самих функций 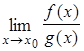, причем они равны между собой, т.е. .

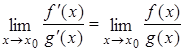В дальнейшем это утверждение будем также называть правилом Лопиталя.

Замечание 1. Правилом Лопиталя можно пользоваться при раскрытии неопределенностей вида (¥-¥), (0×¥), (1^¥), (¥⁰), (0⁰), сводя их к неопределенностям типа , .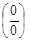

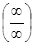Замечание 2. Если после применения правила Лопиталя опять получаем неопределенность вида 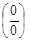или 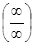, то его можно применить повторно.

Формулы Тейлора и Маклорена.

Теорема. Пусть функция n раз дифференцируема в окрестности точки x₀. Тогда в этой окрестности для функции справедлива следующая формула Тейлора:

+

+ .

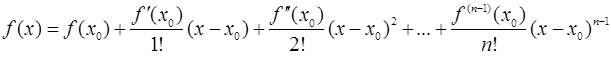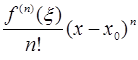Здесь 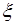некоторая точка, заключенная между 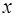и 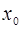(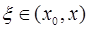), зависящая от 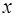, а 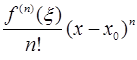= 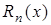- остаточный член в форме Лагранжа.

Доказательство: Обозначим через 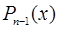многочлен

.

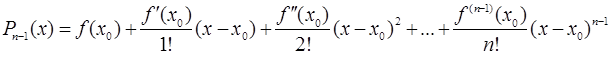Ясно, что для каждого выбранного 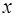существует такое число , для которого будет выполняться равенство:

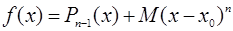. (1)

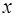Покажем, что это число при уже выбранном будет равно 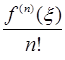при некотором 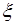из промежутка .

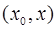Определим функцию

.

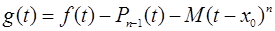Ясно, что

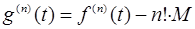
Следовательно, доказательство мы закончим, если покажем, что в некоторой точке 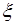(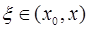) будет выполняться равенство: .

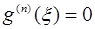Непосредственными вычислениями проверяется (см. многочлен Тейлора!), что для всех 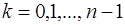выполняются равенства:

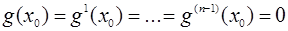(2)

Число выбрано таким образом, чтобы выполнялось равенство (1) и, следовательно, 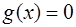. Таким образом, для функции 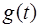на промежутке

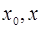[ ] выполняются все условия теоремы Ролля. Следовательно, на интервале (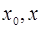) существует такая точка 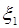, производная функции 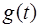, в которой равна нулю, то есть 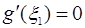. Но тогда с учетом (2) теорему Ролля можно применить к функции 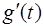на промежутке [ 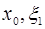] и так далее. Применяя, в конце концов, теорему Ролля к функции 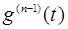на соответствующем промежутке, получим точку 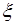, для которой будет справедливо равенство .

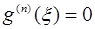Утверждение доказано.

Если x₀=0, то формула Тейлора превращается в формулу Маклорена:

+

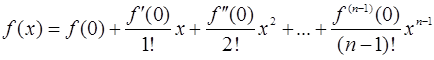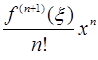
Заметим, что числа n могут выбираться различными, в зависимости и от наличия у функции производных соответствующего порядка, и от необходимой точности расчетов. Например, формула Тейлора для n=4 будет иметь вид:

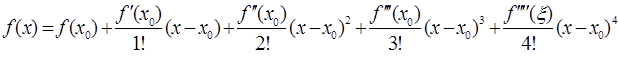
Разложение некоторых элементарных функций по формуле Маклорена.

1. .

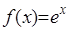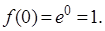
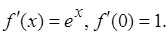
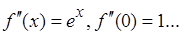
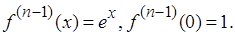
Þ ,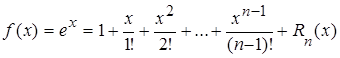

где .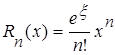

2. .

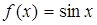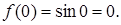
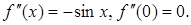
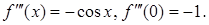
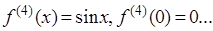
Þ ,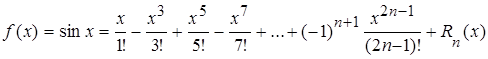

где .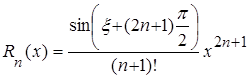

3. .

,…

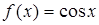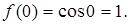
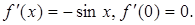
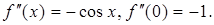
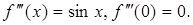
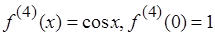Þ ,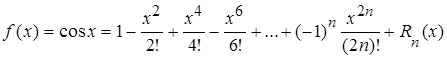

где .

Пусть функция определена и непрерывна на промежутке (a;b).

Определение: Функция называется неубывающей (невозрастающей) на (a;b), если для любых x₁<x₂, принадлежащих (a;b), выполняется ().

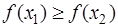Определение: Функция называется возрастающей (убывающей) на (a;b), если для любых x₁<x₂, принадлежащих (a;b), выполняется ().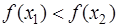

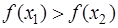Теорема 1.

Для того чтобы функция , дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е. 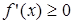, и достаточно, чтобы .

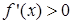Доказательство:

Необходимость.

Пусть f(x) возрастает на (a;b). Тогда для любых 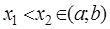выполняется .

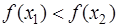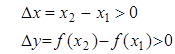Þ Þ .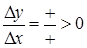

По определению производной: .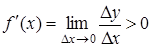

Достаточность.

Пусть 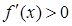на (a;b). f(x) дифференцируема на (a;b). Выберем на этом промежутке 2 точки х₁; х₂.

Тогда на (х₁; х₂) выполняется условие теоремы Лагранжа:

существует точка с Î(х₁; х₂) такая, что .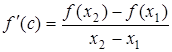

Þ 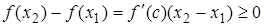(т.к. ).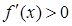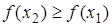

Þ . Þ 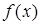возрастает на (a;b).

Ч.т.д.

Теорема 2.

Для того чтобы функция , дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке 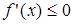и достаточно, чтобы .

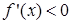Достаточное условие экстремума.

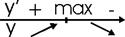
Пусть функция определена в критической точке x₀ и дифференцируема в некоторой окрестности этой точки, за исключением, может быть, самой x₀. Если «при переходе» через точку x₀ слева направо производная меняет знак с плюса на минус, то x₀ – точка максимума; с минуса на плюс – точка минимума.

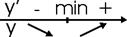
Доказательство:

Пусть производная меняет знак с «+» на «-».

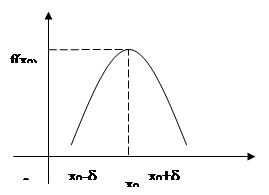Тогда слева от х₀, т.е. на (х₀-δ,х₀) .

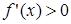Þ слева от х₀ функция 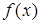возрастает.

Справа от х₀, т.е. на (х_0, х₀+δ) .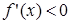

Þ справа от х₀ функция 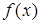убывает.

Т.о. в окрестности точки х₀ выполняется

неравенство .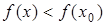

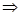х₀ – точка локального максимума.

Аналогично доказывается для минимума.

Ч.т.д.

Наибольшее и наименьшее значения функции на отрезке.

Пусть функция определена и непрерывна на замкнутом промежутке [a;b] и имеет внутри этого промежутка конечную производную.

Тогда по второй теореме Вейерштрасса она на этом отрезке принимает свои наибольшее и наименьшее значения.

Очевидно, что эти значения могут достигаться либо в критических точках, либо на концах отрезка.

Поэтому для нахождения наибольшего и наименьшего значений функции применяют следующий алгоритм решения:

1. Находим критические точки функции. Отбираем те точки, которые принадлежат данному отрезку.

2. Вычисляем значения функции в найденных точках.

3. Вычисляем значения функции на концах отрезка.

4. Из полученных значений функции выбираем наибольшее и наименьшее.

Признак выпуклости.

Пусть функция имеет на интервале (a;b) непрерывную производную второго порядка. Если 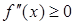, то функция выпукла на промежутке (a;b). Если 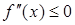, то функция вогнута на промежутке (a;b).

Доказательство:

Пусть для определенности на (a;b) .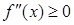

Возьмем точку x₀Î(a;b) и составим уравнение касательной к графику функции в точке с абсциссой x₀:

(1)

Разложим функцию 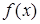в окрестности точки x₀ по формуле Тейлора, причем возьмем два члена разложения и остаточный член:

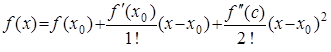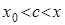, (2)

Вычтем (2) - (1):

.

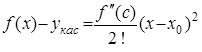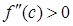на (a;b) .

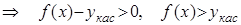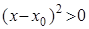
График функции проходит над касательной.

Тогда по определению: функция выпукла.

Вогнутость доказывается аналогично.

Ч.т.д.

Замечание: Условие 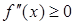(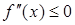) является не только достаточным, но и необходимым для выпуклых (вогнутых) функций.

Определение: Точка, отделяющая промежуток выпуклости функции от промежутка ее вогнутости, называется точкой перегиба.

Необходимые условия существования точки перегиба функции.

Пусть функция 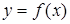в точке x₀ имеет точку перегиба. Если в этой точке существует производная второго порядка, то она обращается в ноль или не существует.

Точки перегиба следует искать среди точек, вторая производная которых равна нулю (y²=0) или не существует. Такие точки называются критическими точками второго рода.

Достаточное условие точки перегиба функции.

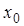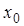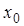
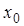Пусть непрерывна в окрестности точки , за исключением, может быть, самой точки . Если «при переходе» через меняет знак, то точка — точка перегиба.

Доказательство:

Пусть «при переходе» через точку 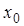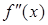меняет знак с «+» на «-».

Тогда слева от точки 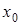— функция выпукла, а справа — вогнута. Тогда по определению: точка 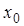— точка перегиба.

Ч.т.д.

Асимптоты графика функции.

Определение: Прямая l называется асимптотой графика функции , если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.

Асимптоты бывают вертикальные, горизонтальные, наклонные.

Вертикальной асимптотой называется прямая x=a, если .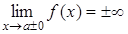

Находят вертикальную асимптоту по точкам разрыва второго рода (бесконечный разрыв).

Наклонной асимптотой называется асимптота, уравнение которой имеет вид: .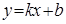

Оказывается, что если 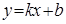является асимптотой, то и 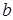в уравнении определяются следующим образом , .

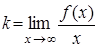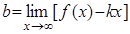Доказательство:

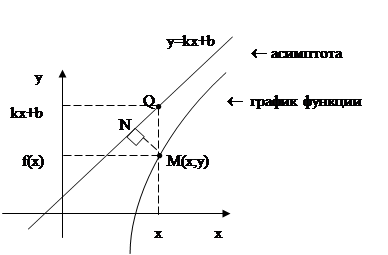
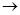По определению асимптоты: если ОМ , то |MN| 0.

Þ |MQ|→0 при x→±∞, т.к. .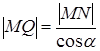

По чертежу: .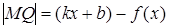

Перейдем к пределу при x→±∞:

(*)

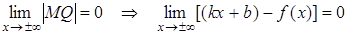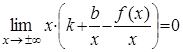
Þ .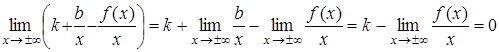

.

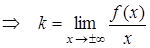Из (*) Þ .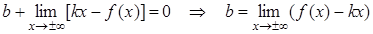

Ч.т.д.

Замечание 1: Чтобы у кривой были наклонные асимптоты, нужно, чтобы соответствующие пределы в определении k и b были конечными, причем предел при x→+∞ и предел при x→-∞ нужно вычислять отдельно.

Замечание 2: Если k=0, то y=b. Наклонная асимптота в этом случае называется горизонтальной.

Замечание 3: Кривая никогда не пересекает вертикальную асимптоту, а горизонтальные и наклонные асимптоты кривая может пересекать и даже бесконечное число раз.

Схема полного исследования функции.

1. Определить естественную область D(y) определения функции.

2. Исследовать на четность и нечетность.

3. Найти точки пересечения графика функции с осями координат.

4. Найти асимптоты.

5. Найти интервалы возрастания и убывания функции, точки экстремума.

6. Найти интервалы выпуклости графика, точки перегиба.

7. Построить график функции.

 

Date: 2015-07-02; view: 863; Нарушение авторских прав