
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методика обучения учащихся решению тригонометрических уравнений и неравенств
В математике тригонометрические функции часто определяются аналитическим путем: с помощью степенных рядов, как решения дифференциального уравнения, как интегральные представления. Тригонометрические функции могут быть определены геометрическими средствами. Существуют различные варианты изложения элементов тригонометрии в школьном курсе математики. Они основаны на применении системы координат, векторов, геометрических преобразований.
Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного треугольника; 2) затем введенные понятия обобщаются для углов от 0° до 180°; 3) тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
Далее вводятся определения тригон. Ф. Конкретнее рассмотрим введение определения cos а, придерживаясь следующей методической схемы: 1) построить на миллиметровой бумаге прямоугольный треугольник ABC; 2) обозначить величину острого угла А буквой а; 3) измерить (по клеткам) прилежащий катет АС и гипотенузу АВ; 4) вычислить отношение 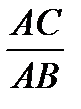 ; 5) записать значение cos а (делается следующая запись: cos a
; 5) записать значение cos а (делается следующая запись: cos a 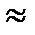 ..., в которой для а не указывается его конкретное значение); 6) измерить транспортиром угол а, найти его величину и записать значение косинуса этого угла данного прямоугольного треугольника; 7) проделать пп. 1—6 для острых углов других прямоугольных треугольников. Определенные трудности в изучении элементов тригонометрии порождает следующая теорема: «Косинус угла а зависит только от градусной меры угла». Необходимость изучения данной теоремы можно разъяснить учащимся следующим образом. Пусть требуется на основании определения найти cos 37°. Предположим что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 37°, они построят прямоугольный треугольник (каждый свой) с углом в 37° измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 37°. Есть ли гарантия что каждый ученик получит один и тот же ответ? Этот[ вопрос возникает по той причине, что каждый ученщ строит свой прямоугольный треугольник, получает свое значения длин прилежащего катета и гипотенузы. Так может быть, и искомое отношение у каждого ученика буде какое-то свое? Понятно, что если бы значение cos 37е при переходе от одного прямоугольного треугольника другому изменялось, то ценность такого понятия в математике была бы невелика. Изучаемая теорема является ответом на поставленные вопросы. Она утверждает, что' косинус острого угла зависит не от выбора прямоугольного треугольника, а только от меры угла.
..., в которой для а не указывается его конкретное значение); 6) измерить транспортиром угол а, найти его величину и записать значение косинуса этого угла данного прямоугольного треугольника; 7) проделать пп. 1—6 для острых углов других прямоугольных треугольников. Определенные трудности в изучении элементов тригонометрии порождает следующая теорема: «Косинус угла а зависит только от градусной меры угла». Необходимость изучения данной теоремы можно разъяснить учащимся следующим образом. Пусть требуется на основании определения найти cos 37°. Предположим что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 37°, они построят прямоугольный треугольник (каждый свой) с углом в 37° измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 37°. Есть ли гарантия что каждый ученик получит один и тот же ответ? Этот[ вопрос возникает по той причине, что каждый ученщ строит свой прямоугольный треугольник, получает свое значения длин прилежащего катета и гипотенузы. Так может быть, и искомое отношение у каждого ученика буде какое-то свое? Понятно, что если бы значение cos 37е при переходе от одного прямоугольного треугольника другому изменялось, то ценность такого понятия в математике была бы невелика. Изучаемая теорема является ответом на поставленные вопросы. Она утверждает, что' косинус острого угла зависит не от выбора прямоугольного треугольника, а только от меры угла.
При решении прямоугольных треугольников необходимо обратить внимание учащихся на тот факт, что с каждой из формул для cos a, sin а и tg а связываются еще две формулы:
Всего, таким образом, получается девять формул. Назовите (с учетом приведенных выше формул) основные виды задач на решение прямоугольного треугольника.
Разработайте опорный конспект для доказательства следующих тригонометрических тождеств:
sin2 a +cos2 a = 1, tg2 a +1 = 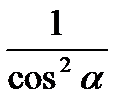 , 1 +
, 1 + 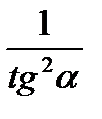 =
= 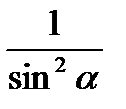
sin (90° — a) = cos a, cos (90° — a) = sin a.
Определения косинуса, синуса и тангенса углов от 0° до 180° являются генетическими. В этих определениях указываются построения и вычисления, позволяющие найти значение тригонометрической функции. В пособии [23] говорится следующее: «До сих пор значения синуса, косинуса и тангенса были определены только для острых углов. Теперь мы определим их для любого угла от 0° до 180°. Возьмем окружность на плоскости ху с центром в начале координат и радиусом R. Пусть а — острый угол, который образует радиус ОА с положительной полуосью х. Пусть х и у — координаты точки А. Значения sin a, cos ос и tg а для острого угла а выражаются через координаты точки А. Именно:
cos a = 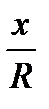 Sin a=
Sin a=  Tg a=
Tg a= 
Определим теперь значения sin a, cos a и tg a этими формулами для любого угла а. (Для tg а угол а = 90° исключается.). В курсе алгебры и начал анализа осуществляется последний, заключительный этап изучения тригонометрических функций. В него входят: 1) закрепление представлений учащихся о радианной мере угла; отработка навыков перехода от градусной меры к радианной и наоборот; 2) формирование представлений об углах с градусной мерой, большей 360°; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа); 3) описание тригонометрических функций на языке радианной меры угла; 4) утверждение функциональной точки зрения на cos a, sin а и tg а (трактовка cos a, sin а и tg а как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т. д.); 5) повторение известных и ознакомление с новыми тригонометрическими тождествами, ключом к которым является тождество cos (а + р) = cos а cos (3 — sin а sin (3 (формула косинуса суммы двух аргументов); 6) применение тригонометрических тождеств в тождественных преобразованиях и при решении задач по стереометрии.
Вопрос
Теория последовательностей занимает в школьном курсе мат-ки значительное место с простейшими примерами числовых последовательностей учащиеся встречаются при рассмотрении в курсе алгебры 9 кл.
темы «Арифметические и геометрические прогрессии». Дальнейшее изучение бесконечных последовательностей, их пределов происходит в курсе алгебры и начала анализа 10 кл. в теме «Действительные числа» бесконечные последовательности и их пределы. Понятия последовательности и ее предела являются основным понятием математического анализа и находит важнейшее применение в различных вопросах школьного курса. Не используя указанных понятий нельзя достаточно строго и полно изложить в школе ряд вопросов алгебры и геометрии, например: вопросы о бесконечных десятичных дробях, о бесконечной прогрессии, о длине окружности, площади плоской фигуры, об объеме пирамиды и т.д. Понятие последовательности вводится в курсе алгебры 9 кл. Причем общие сведения о последовательностях даются в том объеме, который необходим для изучения арифметической и геометрической прогрессии. Для введения понятия последовательности учащимся можно предложить выполнить следующие задания: выписать в порядке возрастания: а) положительные четные числа; 2 4 6 8 … б)положительные нечетные числа; 1 3 5 7 ….Получили последовательности чисел. Числа, образующие последовательности называют членами. Пронумеруем все члены последовательности по порядку: 1,2,3,4..,n,.. например 2,4,6,8,…2n; 1,2,3,4…n. Число аn называют n-ным членом последовательности, саму последовательность обозначают (аn). Последовательность может быть конечной и бесконечной. В ходе решения примеров, учащиеся знакомятся со способами задания последовательности: 1) ф-ла n-ного члена; 2) рекуррентным способом. В этом случае для задания последовательности надо указать 1-ый член последовательности и рекуррентное соотношение выражающие n-ный член последовательности через предыдущий. Рассматривая различные последовательности выделяют те в которых каждый член начиная со второго получается прибавлением к предыдущему члену некоторого числа или умножением предыдущего члена на некоторое число и дают им особое название арифметическая и геометрическая прогрессии.
Вопрос
Понятие интеграла в школе. Цель – ознакомить учащихся с интегрированием, как операцией обратной диф-ию, показать применение интеграла к решению геом задач. Место темы в программе: интеграл вводится на основе рассмотрения задач о площади криволинейной трапеции и построении интегральных сумм. Формула Ньютона – Лейбница вводится на основе наглядных представлений. Применяют интеграл при рассмотрении задач о вычислении площадей и объемов, формула объема шара используется в курсе геом. Методические особенности: при изучении темы целесообразно применять графические иллюстрации. Основные З и У: определение первообразной, простейшие правила нахождения первообразной. Введение понятия интеграла. Интеграл вводится с двух сторон: 1. Через криволинейную трапецию S(х) – есть функция от х, если х придать приращение D х, то получим площадь DS (х)»Dх* f(х), тогда f(х)»DS (х)/ Dх. Отсюда следует, что S|(х)=f(х), то есть площадь есть первообразная от f(х)=> S(х)=F(b)-F(a) – приращение первообразной. 2. С другой стороны – площадь криволинейной трапеции рассматривается как интеграл S= интеграл от а до bf(х)dх. Из первого и второго получаем формулу Ньютона – Лейбница. Схема изложения интегралов в учебном пособии. 1. Площадь криволинейной трапеции как приращение первообразной непрерывной функции на отрезке: понятие криволинейной трапеции, теорема дающая один из подходов к задаче нахождения площади криволинейной трапеции. 2. Интеграл: второй подход к задаче нахождения площади криволинейной трапеции (предел суммы площадей прямоугольников), понятие интеграла как числа к которому стремятся суммы площадей прямоугольников при n -> к бесконечности. Устанавливается связь между интегралом и площадью криволинейной трапеции. 3. Формула Ньютона – Лейбница: сравнение результатов решения задачи о площади криволинейной трапеции при двух рассмотренных подходах дает данную формулу. При изучении данной темы следует широко использовать таблицы, кодопозитивы с изображением криволинейной трапеции, обращение записи решений и т.д. Обращается внимание учащихся на то, что понятие интеграла используется не только при вычислении площадей фигур, но и объемов тел. А также в задачах на вычисление пути за некоторый промежуток времени, если известна скорость, задачах о давлении в жидкостях и др.
Вопрос
Изучение геометрического материала в V классе имеет целью обобщить полученные учащимися в I - IV классах представления о простейших геометрических фигурах, а также познакомить учащихся с новыми геометрическими понятиями. В VI классе большое внимание уделяется систематизации геометрического материала. В пропедевтическом курсе геометрии формируется умения и навыки геометрических построений с помощью линейки, циркуля, чертежного треугольника и транспортира.
Введение и формирование геометрических понятий в V-
VI классах осуществляется на основе индуктивных рассуждений, требующих от начинающего учителя владения соответствующими приемами обучения:
1) выполнение мыслительных операций анализа, синтеза, обобщения, абстрагирования и др.;
2) сосредоточение внимания учащихся на существенные признаки изучаемого понятия;
3) выявление логической структуры признаков вводимого понятия;
4) определение понятий через род и видовые отличия, через описание процесса его образования;
5)построение объекта по существенным признакам понятия
6) дополнительные построения с целью получения объектов, принадлежащих к данному понятию;
7) рассмотрение объекта в плане разных понятий и др.
Будущий учитель должен знать признаки сформированности геометрических понятий у учащихся. К ним относится в основном следующая совокупность умений учащихся:
а)умение самостоятельно выделять существенные признаки объекта;
б)давать определение понятию;
в)строить объект, исходя из существенных признаков понятия;
г)выполнять дополнительные построения с целью получения объекта, принадлежащего данному понятию и др.
Формируются указанные умения в основном с помощью задач. При этом будущий учитель должен знать, что ряд геометрических понятий пропедевтического курса геометрии получает генетическое определение (описанием процесса их образования). Геометрические понятия, как отрезок, луч, равносторонний треугольник, координатный луч, равные фигуры, площадь прямоугольника и квадрата, объем прямоугольного параллелепипеда, окружность, дуга окружности, сектор, угол, равные углы, длина окружности, площадь круга, определяются описанием процесса их образования т.е.генетически. Геометрические понятия, как, длина ломаной, периметр многоугольника, квадрат, круг, биссектриса угла, развернутый угол, прямой угол, градус, острый угол, тупой угол, перпендикулярность и параллельность прямых и др. определяются через видовые отличия т. е. через род.
В учебниках имеет место еще один способ определения - описание понятия. Под описанием понятия имеют в виду перечисление всех его элементов. Нестрого под описанием понимают выражение содержания с помощью понятий, не являющихся предшествующими и используемых индуктивно.
Вопрос
Первые уроки планиметрии. Методика работы с аксиомами и теоремами.
Одна из целей включения аксиом в школьный учебник – сформировать базу для построения доказательств. Удачно подобранная система аксиом призвана обеспечить рациональное и простое построение всего курса. Аксиома - это мат. предложение, принимаемое без док. Они образуют систему отправных исходных положений. К системе аксиом предъявляются требования: независимости, непротиворечивости, целостности. Методическая схема введении аксиом:1.ввести аксиому на наглядной основе; 2.сформулировать аксиому; 3. выполнить логический анализ формулировки аксиом.; 4. провести математический. диктант. Математическое положение, истинность которого устанавливается посредством доказательства наз.теоремой, в Т. указано при каких условиях рассматривается объект (условие Т.), что об этом в Т-е утверждается (заключение). Формулировка Т может быть условной (если, то) и категорической. Доказательство - это организованная система предложений, каждая из кот является.либо аксиомой, либо выводится из 1-го или нескольких предложений по правилам логики. Под обучением доказательства понимают обучение мыслительным процессам поиска нахождения и построения доказательства. Этапы работы над Т.:1.мотивация необходимости изучения и раскрытия содержания 2.работа над структурой З.мотивация необходимости доказательства 4.построение чертежа и краткая запись условия Т. б.поиск доказательства, доказательство, запись.6.работа по закреплению Т.7.применение Т. Методы док.: аналитический (сведение к известному утверждению), синтетический (приведение к данному утверждению), аналитико-синтетический, от противного.
Вопрос
Треугольник — самый «экономный» вид многоугольника. Для его задания достаточно указать его вершины — три точки, не лежащие на одной прямой, или три попарно пересекающиеся прямые. Классифицируют треугольники также по степени их симметричности или по числу равных сторон.
| Треугольник | Количество осей симметрии | Количество парравных сторон |
| Равносторонний | ||
| Равнобедренный | ||
| Разносторонний | Нет | Нет |
В школе принята также классификация треугольников по углам: остроугольные, прямоугольные и тупоугольные.
Изучение треугольников в соответствии с программой распределено практически по всем классам неполной средней школы. Курс VI класса — это, по существу, геометрия треугольника. Треугольник — одна из основных «рабочих» фигур изучаемого в школе курса планиметрии. Установление цепочек равных треугольников — широко используемый прием доказательства различных геометрических утверждений.
На изучение признаков равенства треугольников отводится 12 ч: (один из них резервный). Главная цель изучения этого материала — добиться активного владения им, обратив особое внимание на отработку навыков использования признаков равенства треугольников в решении задач. Равенство треугольников традиционно изучается в курсе планиметрии. В соответствии с определением, данным в учебнике А. В. Погорелова, в равных треугольниках ABC и А1В1С1 имеем шесть пар соответственно равных элементов: АВ — А1В1, ВС = В1С1, АС = А1С1, 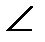 A=
A= 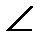 A1,
A1, 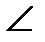 B=
B= 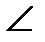 B1,
B1, 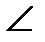 C=
C= 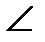 C1.Внимание к записи равенства треугольников (буквы, обозначающие соответственные вершины, должны занимать одинаковые позиции в обозначении треугольников) позволяет: 1) имея запись равенства треугольников, например
C1.Внимание к записи равенства треугольников (буквы, обозначающие соответственные вершины, должны занимать одинаковые позиции в обозначении треугольников) позволяет: 1) имея запись равенства треугольников, например  АВС=
АВС=  PQR, почти автоматически делать вывод о равенстве соответственных сторон и углов, т. е. по определению будем иметь: 1)AB = PQ, BC = QR, AC = PR,
PQR, почти автоматически делать вывод о равенстве соответственных сторон и углов, т. е. по определению будем иметь: 1)AB = PQ, BC = QR, AC = PR, 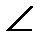 A =
A = 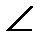 P,
P, 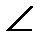 B=
B= 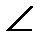 Q. AC— /L.R; 2) существенно опираться на запись равенства треугольников при доказательстве равенства углов при основании в равнобедренном треугольнике и теоремы, обратной ей. Учителю необходимо следить за правильностью буквенной записи равенства треугольников. Характерным для учебного пособия является и наличие в нем аксиомы существования треугольника, равного данному (которая, по существу, является эквивалентом аксиомы подвижности плоскости). Важным на начальном этапе рассмотрения равных треугольников является отработка понятий «сторона, противолежащая углу», «угол, заключенный между сторонами». Программа диктует необходимость уже с самого начала изучения систематического курса планиметрии проводить работу по логическому развитию учащихся, по формированию и развитию таких понятий, как «свойство» и «признак». Доказательство первых двух признаков равенства треугольников в учебном пособии сводится к доказательству совпадения некоторого третьего треугольника, равного первому и определенным образом расположенного относительно второго, с этим вторым данным треугольником. При доказательстве первых двух признаков равенства можно использовать серию рисунков (кодопозитивов), отражающих динамику доказательства, отдельные его этапы. Так, при рассмотрении первого признака полезно использовать серию рисунков. При использовании признаков равенства треугольников: 1) указывается пара треугольников, относительно которых выдвигается гипотеза об их равенстве; 2) в рассматриваемых треугольниках выделяются пары соответственно равных элементов; 3) на основании одного из признаков делается вывод о равенстве рассматриваемых треугольников; 4) делают вывод о равенстве каких-либо из соответственных элементов. При обучений решению задач на применение признаков равенства треугольников целесообразно использование готовых чертежей, на которых отмечены равные элементы. Теорема Пифагора позволяет широко применять в обучении геометрии Тмётод" координат и другие аналитические методы. Тесно связано с этой теоремой рассмотрение тригонометрических функций острого угла прямоугольного треугольника. Очень важным в раскрытии геометрии треугольника является вопрос о подобии треугольников как конкретизации общего понятия подобных фигур. Этот материал важен с точки зрения формирования представлений о форме фигуры.
Q. AC— /L.R; 2) существенно опираться на запись равенства треугольников при доказательстве равенства углов при основании в равнобедренном треугольнике и теоремы, обратной ей. Учителю необходимо следить за правильностью буквенной записи равенства треугольников. Характерным для учебного пособия является и наличие в нем аксиомы существования треугольника, равного данному (которая, по существу, является эквивалентом аксиомы подвижности плоскости). Важным на начальном этапе рассмотрения равных треугольников является отработка понятий «сторона, противолежащая углу», «угол, заключенный между сторонами». Программа диктует необходимость уже с самого начала изучения систематического курса планиметрии проводить работу по логическому развитию учащихся, по формированию и развитию таких понятий, как «свойство» и «признак». Доказательство первых двух признаков равенства треугольников в учебном пособии сводится к доказательству совпадения некоторого третьего треугольника, равного первому и определенным образом расположенного относительно второго, с этим вторым данным треугольником. При доказательстве первых двух признаков равенства можно использовать серию рисунков (кодопозитивов), отражающих динамику доказательства, отдельные его этапы. Так, при рассмотрении первого признака полезно использовать серию рисунков. При использовании признаков равенства треугольников: 1) указывается пара треугольников, относительно которых выдвигается гипотеза об их равенстве; 2) в рассматриваемых треугольниках выделяются пары соответственно равных элементов; 3) на основании одного из признаков делается вывод о равенстве рассматриваемых треугольников; 4) делают вывод о равенстве каких-либо из соответственных элементов. При обучений решению задач на применение признаков равенства треугольников целесообразно использование готовых чертежей, на которых отмечены равные элементы. Теорема Пифагора позволяет широко применять в обучении геометрии Тмётод" координат и другие аналитические методы. Тесно связано с этой теоремой рассмотрение тригонометрических функций острого угла прямоугольного треугольника. Очень важным в раскрытии геометрии треугольника является вопрос о подобии треугольников как конкретизации общего понятия подобных фигур. Этот материал важен с точки зрения формирования представлений о форме фигуры.
Вопрос
Окружность и круг в школьном курсе геометрии: основные понятия, определения, теоремы, формулы. Методика обучения геометрическим построением с помощью циркуля и линейки. С геом-ми построениями уч-ся знакомятся в конце 7 кл. Но перед этим они изучают понятия окр-ти и круга. В процессе изучения темы уч-ся знакомятся с теорет-ими фактами, связанными с окр-ю, необходимыми для решения задач на построение и для изучения в дальнейшем некоторых вопросов курса, в частности многоугольников, вписанных в окр-ть и описанных около окр-ти. В связи с этим при рассмотрении теор-ого материала и решении задач, необходимо отработать такие вопросы, как рав-во радиусов одной окр-ти, перпендикулярность касательной и радиуса, проведенного в точку касания, положение центров вписанной в треугольник и описанной около треугольника окр-ей. Док-во теорем о центрах вписанной и описанной окр-ей и решение соответствующих задач позволяет обратить внимание уч-ся на важные с точки зрения дальнейшего применения св-ва серединного перпендикуляра к отрезу, биссектрисы угла, отрезков касательных, проведенных к окр-ти из общей точки, радиуса, перпендикулярного хорде. При изучении и закреплении теоремы об углах вписанных в окр-ть, следует обратить внимание на конфигурацию, связанную с вписанным в окр-ть прямым углом, поскольку в дальнейшем эта конфигурация будет часто встречаться уч-ся. Значительное внимание при изучении данной темы должно быть уделено формированию практических навыков построений с помощью циркуля и линейки при решении простейших задач. Кроме того, здесь формируются умения связанные с вычленением основных построений, необходимых для решения комбинированных задач. При решении задач на построение вопрос о существовании и количестве решений не ставиться; задача считается решенной если указана последовательность выполняемых операций и доказано, что получаемая таким образом фигура удовлетворяет условию задачи.
Вопрос
Date: 2015-06-11; view: 1018; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |