
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Группа движений плоскости и ее подгруппы. Группа симметрий фигур
Т:мн-во всех движений плоскости явл.группой преобразования.
Т:мн-во всех двух плоскости І рода-группа преобразований.
Д-во т.к композиции2 движ. І рода сохр.ориентацию плоск.,то она тоже явл.движ І рода.
Движение обратное движению І родп сохр.ориентацию плоскости.
Замеч: мн-во всех движ-ний ІІ рода не явл.группой,т.к. композиция двух движений ІІ рода явл.движ. І рода.
Группа всех движений плоскости содержит подгруппу движений І рода,которая в свою очередь имеет подгруппу:все параллельные переносы,группу поворота с центром.
Опр: пусть Ф -фигура плоскости движ.F плоскости отлична от F≠E наз-ся проеобр. Симметрии фигуры Ф,если F(Ф)=Ф.
Т:мн-во всех проебр.симметр.некоторой фигуры Ф образует группу проебразований.
Замеч: в широком смысле к проебраз. Симмет. Фигуры Ф относ.так же тождеств.проебразование
Опр: группа Ϭ (СИГМА) наз.Группой симметр.фигур.
Если группа симметр.нескольких фигур состоит только из тождественного преобразования то говорят что фигура не обл.симметрией.
Опр: т.О назыв.центрои симметрии Ф,если Zₒ(Ф)=Ф
29.
Гомотетия и ее свойства. Способы задания гомотетии. Аналитическое
выражение гомотетии. Группа гомотетий.
Опр: пусть на плоскости дана некотор.т О, и К≠О
ᵾМ→М′ так что ОМ′(вектор)=K∙ОМ (вектор)
(О→О) полученное проебразование плоск.наз. гомотетией с центром в точке О и коэф. K и обознач. Нₒᵏ.
Гомотетией наз.полож,если k>0 и отр.если k<0
Две фигуры Ф₁ и Ф₂ наз.гомотет.если сущ. Нₒᵏ такая что Ф₂ = Нₒᵏ(Ф₁)
Центром гомотетии фигур Ф₁ и Ф₂ наз.внешними если гомот.полож.и внутренними если она отриц.
Т:гомотетия сохр.простое отношение трех точек.
Св-ва гомотетии:
1)коммутативные отрезки ІІ отн.длинн гомотетичных отрезков равны модулю коэф.
2) гомотетия переводит прямую в прямую.прямая прох. Через центр гомотетии переходит в себя,а не проход.через центр-в парал.прямую.
3)при гомотетии луч переходит в луч.
4)гомо тетия сохр.коллинар.лучей.
5) гомотетия сохр. Величину углов.
6)сохр.ориентац плоскости.
Способы задания гомотетии:
1) Гомотетия можно задать центром и коэф.
2) Можно центром и парой соответс.точек АА′ при этом три точки должны лежать на одной прямой.
Т:мн-во всех гомотетий с уентром в т.О образ.группу.
30.
Определение преобразования подобия. Непосредственным обобщением движений являются преобразования подобия. Преобразование А называется преобразованием подобия, если для этого преобразования существует такое положительное число К- «коэф. подобия», что каковы бы ни были две точки М1 и М2, всегда
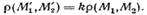
Св-ва: 1 Преобразование подобия устанавливает между точками фигур взаимно однозначное соответствие .2 Если некоторая фигура получена из другой фигуры преобразованием подобия с центром О и коэффициентом подобия К, то и обратно исходная фигура может быть получена преобразованием подобия из второй фигуры с тем же центром подобия и коэфф. подобия К1=1/К. 3 Любые точки, лежащие на одной прямой, преобразуются при гомотетии в точки лежащие на одной прямой параллельной исходной.
31.
Пусть на плоскости фиксирована аффинная система координат 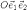 . Преобразование
. Преобразование 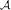 плоскости называется аффинным, если координаты
плоскости называется аффинным, если координаты  образа
образа 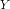 выражаются через координаты
выражаются через координаты 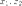 прообраза
прообраза 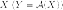 по формулам
по формулам 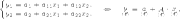
Св-ва: 1При аффинном преобразовании отношение длин параллельных отрезков не изменяется. 2. При аффинном преобразовании прямая линия переходит в прямую линию, отрезок переходит в отрезок, параллельные прямые переходят в параллельные.
32.
Подобием 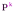 называется такое преобразование пространства, при котором для любых точек пространства X, Y и их образов X´, Y´ выполняется соотношение
называется такое преобразование пространства, при котором для любых точек пространства X, Y и их образов X´, Y´ выполняется соотношение 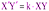 , где k – некоторое фиксированное положительное число (называемое коэффициентом подобия).
, где k – некоторое фиксированное положительное число (называемое коэффициентом подобия).
Фигура Ф называется подобной фигуре Ф´, если существует подобие, переводящее Ф в Ф´ Св-ва:
1. При подобии прямая отображается на прямую, луч – на луч, отрезок – на отрезок, плоскость – на плоскость, полуплоскость – на полуплоскость. 2. Подобие сохраняет величину угла между прямыми, между прямой и плоскостью, между плоскостями. 3. Подобие сохраняет отношение отрезков. 4. Если тело Т´ – образ тела Т при подобии 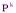 , то V(T´)=k3∙V(T).
, то V(T´)=k3∙V(T).
33.
Главными направл. родства наз. направления двух взаимоперпендик. прямых l и m, которые при родстве переходят в две взаимопренд. прямые l' и m'
34.
АФФИННЫЕ ПРЕОБРАЗОВАНИЯ плоскости α в плоскость α' (или плоскости α в себя, или пространства в себя) есть произведение перспективно-аффинных преобразований (параллельных проекций).
Если точки А, В, С,... плоскости α проектируются в направлении ℓ в точки А0, B0, С0,... плоскости α0 (рис. 19), а точки А0, B0, С0,... проектируются параллельной проекцией в направлении ℓ' в точки А', В', С,... на плоскость α', то соответствие между плоскостями α иα', в котором точкам А, В, С,... плоскости α сопоставляются точки А', В', С',... плоскости α', будет аффинным. Опр. Нетождественное аффинное преобразование называется перспективно – аффинным (родственным), если оно имеет прямую инвариантных точек – ось родства.Определение. Частный случай родства, при котором прямые, соединяющие соответствующие точки родства не параллельны его оси родства называют косым сжатием плоскости, а направление прямых, соединяющее соответствующие точки - направленное сжатие. Теор.Множество всех аффинных преобразований плоскости образует группу аффинных преобразований плоскости. Основным инвариантом группы аффинных преобразований является простое отношение трех точек плоскости. Теор. Множество всех аффинных преобразований плоскости образует группу аффинных преобразований плоскости. Основным инвариантом группы аффинных преобразований является простое отношение трех точек плоскости. Определение. Две фигуры 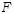 и
и 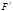 называются аффинно-эквивалентными, если существует аффинное преобразование
называются аффинно-эквивалентными, если существует аффинное преобразование 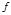 такое, что
такое, что 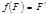 . Теор. Два четырехугольника аффинно-эквивалентные, тогда и только тогда, когда их можно обозначить через
. Теор. Два четырехугольника аффинно-эквивалентные, тогда и только тогда, когда их можно обозначить через 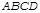 и
и  ,
, 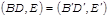 , где
, где 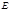 и
и 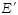 - точки пересечения прямых
- точки пересечения прямых 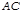 и
и 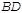 ,
, 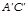 и
и 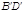 .Теор. Любые два эллипса, гиперболы аффинно-эквивалентны.
.Теор. Любые два эллипса, гиперболы аффинно-эквивалентны.
35.
Утверждение
Композиция аффинных преобразований есть снова аффинное преобразование:
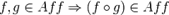
Мы здесь использовали значок « » композиции. Выражение
» композиции. Выражение 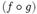 следует понимать как преобразование плоскости, которое получается после применения преобразования
следует понимать как преобразование плоскости, которое получается после применения преобразования 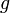 и последующего применения преобразования
и последующего применения преобразования  . Значок «
. Значок « » следует читать как «принадлежит», то есть «содержатся внутри как элемент».
» следует читать как «принадлежит», то есть «содержатся внутри как элемент».
36.
37.
Построения с помощью циркуля и линейки — раздел евклидовой геометрии, известный с античных времён. В задачах на построение циркуль и линейка считаются идеальными инструментами, в частности: Линейка не имеет делений и имеет сторону бесконечной длины, но только одну. Циркуль может иметь сколь угодно большой или сколь угодно малый раствор (то есть может чертить окружность произвольного радиуса). Выделить точку из множества всех точек: 1.произвольную точку; 2.произвольную точку на заданной прямой; 3.произвольную точку на заданной окружности; 4.точку пересечения двух заданных прямых; 5.точки пересечения/касания заданной прямой и заданной окружности; 6.точки пересечения/касания двух заданных окружностей «С помощью линейки» выделить прямую из множества всех прямых: 1.произвольную прямую; 2.произвольную прямую, проходящую через заданную точку; 3.прямую, проходящую через две заданных точки «С помощью циркуля» выделить окружность из множества всех окружностей: 1.произвольную окружность; 2.произвольную окружность с центром в заданной точке; 3.произвольную окружность с радиусом, равным расстоянию между двумя заданными точками; 4.окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками
38.
1)Анализ на этом этапе устанавливают зависимости между данными задачи и исконной фигуры. Начинают анализ с выполнения искиза.2) Построение на этом этапе перечисляют те шаги которые нужно выполнить для решения задачи затем эти шаги выполняют с помощи циркуля и линейки начинается это построение с выбора данных.[AB]-отрезок,(АВ)-прямая,[АВ)-луч. 3)На этом этапе доказывают что построенная фигура удовлетворяет всем требованиям задачи. 4) Это этап исследования на этом этапе выясняют сколько решений и какие имеет задача.
39.
Сущность метода–путем рассуждений выясняем что построение искомой фигуры сводится к одной точке(х) которая удовлетворяет условию (αи β). Так как (х) удовлетворяет условию α и β одновременно то х€F1∩F2.При решении задач на построение метода пересечение могут встречается 1)Множество точек удоленых на расстоянии r от O окружность центра точки O радиуса r.2) Множество точек плоскости равноудоленых от точек А и В.3)Множество точек плоскости равноудаленной от данной прямой это пара прямых параллельно данной.
40.
Решение задач на построение заключается в следушем, на ряду с данными фигурами F1,F2,…,Fn и искомой фигурой F рассматривают так же образы этих фигур при некотором преобразовании плоскости N. В качестве преобразовании N может выступать любое движение плоскости либо гомотетий так возникаю методы осевой симметрии, параллельного переноса
41.
Основная идея метода подобия состоит в следующем:Сначала строят фигуру, подобную искомой так, чтобы она удовлетворяла всем условиям задачи, кроме одного. Затем строят уже искомую фигуру, подобную искомой и удовлетворяющую опущенному требованию.Метод подобия находит применение обычно в случаях, когда среди данных лишь одно является отрезком, а все остальные данные-либо углы, либо отношения отрезков.Обычно целесообразно вспомогательную фигуру строить так, чтобы она была подобна не только искомой, но и подобно расположена с ней. Успех решения зависит в этих случаях от выбора центра подобия.При решении задач на построение методом подобия часто воспользоваться следующим замечанием. Если две фигуры подобны, то коэффициент подобия равен отношению любых двух соответствующих отрезков. Если отрезкам a, b, c,… фигуры Ф соответствуют отрезки a1, b1, c1,… подобной фигуры Ф1, то коэффициент подобия равен также отношениям: При решении каждой сколько-нибудь сложной задачи на построение возникает вопрос о том, как нужно рассуждать, чтобы разыскать способ решения задачи, чтобы получить все решения задачи, чтобы выяснить условия возможности решения задачи и т.п. Поэтому при решении конструктивных задач в учебных условиях рекомендуется пользоваться известной схемой решения, состоящей из следующих четырех этапов: 1) анализ; 2) построение; 3) доказательство; 4) исследование.
44.
Теорема: Если какой-либо корень приведенного куб. ур-ния (x3+ax2+bx+c=0)можно построить с помощью циркуля и лин-ки, то это ур-е имеет один рац.корень.
Для решеня задач исп. след теорема.
Теорема: Если перевед. куб. ур-е с рац. коэфиц. не имеет рац. корня, то не один его корень не может быть построен при помощи циркуля и линейки.
Задача 1: (об удвоении куба)
Построить сторону куба, объем кот-го в два раза больше чем объем дан. куба.
Решение:
Пуст А-ребро дан-го куба
х-ребро иск-го куба, требуется x3-2a3;если принять а за ед. измерения: x3-2=0; ясно, что у этого ур-я 3 корня x1=  ,
,
x2, x3- комплексные=> ур-е не может быть постр. при помощи цир. и лин.
Задача 2 (об трисекции угла)
по делению угла на три равные части. Задачу о трисекции угла достаточно исслед. только для острых углов т.к. α<  ; α=π-β, β-острый угол
; α=π-β, β-острый угол  =
=  -
-  .
.
Таким образом задачча о трисекции угла разрешима только в том случае, когда последнее ур-е (х3-3х-а=0)имеет рац. корень а это имеет место не при любых α например (α=60°).
Задача (об квадратуре круга) построить сторону квадрата S кот-го, равна S круга.
x-стороны иск-го квадрата;
r- радиус дан-го круга;
x2=πr 2; х=r  ; х=
; х=  , r-ед. измерения.
, r-ед. измерения.
Мно-во R дейст.чисел дел-ся на алгебр. и трансендентные, к алгебр. числам отн-ся числа котороые яв-ся корнями с рац. коэфициентами. К трансендентным числа отн-ся числа не яв-ся алгебраич. например (π) Если в задачах на построение длин задан трансендентным числом, то этот отрезок не может быть построен с помощью цирк. и лин-ки.=>задача об квадратуре круга не разрешима при помощи лин-ки и цир-ля.
Построение прав. мног-ов, задача на это построение равносильна задаче о делении ок-ти на n-равных частей n=3,4,6,8,12,24…..
Теорема Гаусса: Постр. прав. n-угольника с помощью цик-ля и лин-ки возможно, ó когда n имеет вид n=2mp1*p2….pi, где n  Z и {0}, pi-число Ферма.(простые различные между собой числа вида (2Zk+1).
Z и {0}, pi-число Ферма.(простые различные между собой числа вида (2Zk+1).
Теорема (Критерий разрешаемости зад. На постр. циркулем и линейкой). Отрезок x может быть построен по данным отрезкам с помощью цир-ля и лин-киó когда длина этого отрезка выраж-ся через длины данных отрезков, рацион. числа с помощью конечного числа арфметич. опер-й (+,-,*,/)и извлеч. квадр. корня.
Опр. Пусть дано выр-е F(a, b,….L)опред. на некоторой области изменения переменных a, b,….L. Говорят, что выражение F явл-ся однороднным выр-м степени k, если 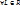 , t≠0 вып-ся соотношения F (ta, tb,…..tL)=t2 *F(a, b,….L)для всех значений a, b,…L из области определения. Алгебраический метод решения здач на постр. заключ в след. (в ходе анализа сводят реш. Задачи к постр. отрезка х, выражают длину отрезка х, через длины известных отрезковпо нек. фор-х, затем по найд. Фор-ле строят отрез. Х цирк-м и лин-й)
, t≠0 вып-ся соотношения F (ta, tb,…..tL)=t2 *F(a, b,….L)для всех значений a, b,…L из области определения. Алгебраический метод решения здач на постр. заключ в след. (в ходе анализа сводят реш. Задачи к постр. отрезка х, выражают длину отрезка х, через длины известных отрезковпо нек. фор-х, затем по найд. Фор-ле строят отрез. Х цирк-м и лин-й)
Теорема: Выражение f(a, b,….L), где а,b,..,L – длины даннных отрезков опред. длину одного и того же отрезка, при любом выборе еденицы измерения, <=>, когда f- однородное выражение 1-ой степени.
Date: 2015-07-01; view: 1883; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |