Метод конечных элементов

Инженерный анализ

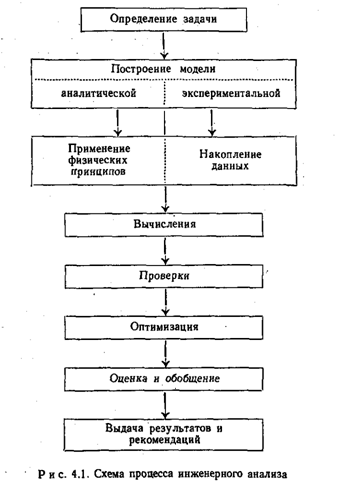
Инженерный анализ, связан с использованием основных физических принципов для решения задач с целью получения за приемлемое время приемлемых решений. Важным положением здесь являются: основные принципы, приемлемое время решения и приемлемое (имеющее смысл) решение. Выполняя инженерный анализ, инженер должен знать об ограничениях, свойственных избранному способу решения задачи. Например, ему необходимо знать, означают ли слова “приемлемое решение”, что полученный результат должен со 100, 10 или 1%-ной вероятностью соответствовать точному (т. е. идеальному) значению. Инженер должен также представлять себе, означает ли “приемлемое время решения” сутки, неделю или год. Кроме того, он должен знать о своих недостатках и сильных сторонах и в возможностях находящихся в его распоряжении вычислительных устройств и аппаратуры для экспериментальной работы.

Основное положение, развиваемое в этой книге, можно сформулировать так: “правильное” решение задачи инженерного анализа “правильным” методом возможно лишь при учете ограничений, с которыми сталкивается инженер, решающий эту задачу. Квалифицированные инженеры при решении задачи выбирают те методы, которые совместимы, с одной стороны, с их целями, а с другой стороны, с ограничениями, свойственными данному способу решения. Эта часть книги до гл. 10 включительно посвящена разработке методики инженерного анализа, в которой главный упор делается на применение основных законов природы (а не на приобретение специальных знаний), на способы принятия допущений и на необходимость понимания ограничений, свойственных тому или иному способу решения задачи.

Состояние системы определяется через совокупность состояний всех ее подсистем, т. е. в конечном счете элементарных подсистем. Элементарные подсистемы бывают двух типов: с конечным и бесконечным числом возможных состояний. Подсистемы первого типа называют также подсистемами с дискретными состояниями, второго типа — с непрерывными состояниями. Примером подсистемы с дискретными состояниями может служить колесико арифмометра или счетчика в такси. Нормально это колесико находится в одном из десяти положений, соответствующих десяти цифрам от 0 до 9. Время от времени оно поворачивается и переходит из одного состояния в другое. Этот процесс поворота нас мало интересует. Правильная работа системы (арифмометра, счетчика) зависит только от того, как связаны между собой «нормальные» положения колесиков, а как происходит переход из одного положения (состояния) в другое — несущественно. Поэтому мы и можем рассматривать арифмометр как систему, элементарные подсистемы которой могут находиться только в дискретных состояниях. Современная быстродействующая цифровая вычислительная машина также состоит из подсистем (триггерных схем) с дискретными состояниями. Все, что мы знаем в настоящее время о нервной системе животных и человека, указывает на то, что решающую роль в ее работе играет взаимодействие подсистем (нейронов) с дискретными состояниями.

С другой стороны, человек, катящийся на велосипеде, или аналогичная вычислительная машина дают нам примеры систем, которые описываются как состоящие из подсистем с непрерывными состояниями. В случае велосипедиста таковыми являются все движущиеся друг относительно друга части велосипеда и человеческого тела: колеса, педали, руль, ноги, руки и т. д. Их состояния — это их положения в пространстве, описывающиеся координатами (числами), которые могут принимать непрерывные множества значений.

Если система состоит исключительно из подсистем с дискретными состояниями, то и сама она может находиться лишь в конечном числе состояний, т. е. является системой с дискретными состояниями. Такие системы мы будем называть просто дискретными системами, а системы с непрерывным множеством состояний — непрерывными. Дискретные системы во многих отношениях проще для анализа, чем непрерывные. В частности, пересчет числа возможных состояний системы, который играет важную роль в кибернетике, требует в дискретном случае лишь знания элементарной арифметики. Пусть дискретная система A состоит из двух подсистем a и a, причем подсистема a может иметь n, а подсистема a — n возможных состояний. Допуская, что каждое состояние системы a может сочетаться с каждым состоянием системы a, мы находим, что число N возможных состояний системы A есть nn.

Если система A состоит из m подсистем a, где i = 1, 2,..., m, то N = nn... n.

В дальнейшем мы будем рассматривать только дискретные системы. Кроме того прагматического соображения, что они принципиально проще, чем непрерывные системы, существует еще два довода в пользу целесообразности такого ограничения.

Во-первых, все непрерывные системы можно, в принципе, рассматривать как дискретные системы с чрезвычайно большим числом состояний. В свете тех знаний, которые дала нам квантовая физика, такой подход даже следует рассматривать как теоретически более правильный. Причина, по которой непрерывные системы все же не исчезают из кибернетики, — это наличие весьма совершенного аппарата — математического анализа и, в первую очередь, дифференциальных уравнений для рассмотрения таких систем.

Во-вторых, самые сложные кибернетические системы, как возникшие естественным путем, так и созданные руками человека, неизменно оказываются дискретными. Особенно наглядно это видно на примере животных. Относительно простые биохимические механизмы, регулирующие температуру тела, содержание в крови различных веществ и т.п., являются непрерывными, но нервная система устроена по дискретному принципу.

Метод конечных элементов (МКЭ) — это численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.

Суть метода следует из его названия. Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.

Если говорить в матричных терминах, то собираются так называемые матрицы жёсткости (или матрица Дирихле) и масс. Далее на эти матрицы накладываются граничные условия (например, при условиях Неймана в матрицах не меняется ничего, а при условиях Дирихле из матриц вычёркиваются строки и столбцы, соответствующие граничным узлам, так как в силу краевых условий значение соответствующих компонент решения известно). Затем собирается система линейных уравнений и решается одним из известных методов.

С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвейдиакоптики — общего метода исследования систем путём их расчленения.

Пусть в одномерном пространстве Р1 необходимо решить следующее одномерное дифференциальное уравнение для нахождения функции на промежутке от 0 до 1. На границах области значение функции равно 0:

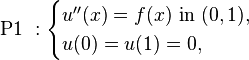
где известная функция, неизвестная функция от 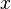. вторая производная от по 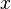. Решение поставленной задачи методом конечных элементов разобьём на 2 этапа:

· Переформулируем граничную задачу в так называемую слабую (вариационную) форму. На этом этапе вычислений почти не требуется.

· На втором этапе разобьём слабую форму на конечные отрезки-элементы.

После этого возникает проблема нахождения системы линейных алгебраических уравнений, решение которой аппроксимирует искомую функцию.

Если есть решение, то для любой гладкой функции , которая удовлетворяет граничным условиям в точках и , можно записать следующее выражение:

(1)

С помощью интегрирования по частям преобразуем выражение (1) к следующей форме:

(2)

Оно получено с учётом того, что .

Разобьём область, в которой ищется решение

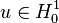такое, что

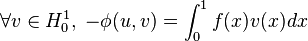
на конечные промежутки, и получим новое пространство :

(3) 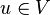такое, что

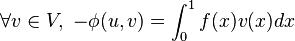
где кусочная область пространства 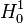. Есть много способов для выбора базиса . Выберем в качестве базисных функций такие , чтобы они представлялись прямыми линиями (полиномами первой степени):

для (в данном примере )

Если теперь искомое приближённое решение представить виде 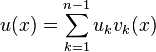, а функцию 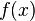аппроксимировать как , то с помощью (3) можно получить следующую систему уравнений относительно искомых :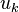

,

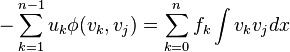где .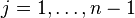

Преимущества и недостатки[править | править вики-текст]

Метод конечных элементов сложнее метода конечных разностей в реализации. У МКЭ, однако, есть ряд преимуществ, проявляющихся на реальных задачах: произвольная форма обрабатываемой области; сетку можно сделать более редкой в тех местах, где особая точность не нужна.

Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники (погрешность, в зависимости от вариации метода, обратно пропорциональна синусу или самого острого, или самого тупого угла в разбиении). Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне), что дало возможность создавать полностью автоматические конечноэлементные САПР.

Различают три варианта постановок задач теории упругости.

1. Постановка задач теории упругости в перемещениях

Основные неизвестные — три компоненты вектора перемещений (в дальнейшем — перемещения). Они должны удовлетворять трём уравнениям равновесия, записанным в перемещениях (уравнения Ламе). В каждой неособенной точке поверхности тела перемещения должны удовлетворять трём граничным условиям. Граничные условия могут быть сформулированы в трёх вариантах:

· заданы перемещения;

· заданы комбинации напряжений, записанные через нормальные и касательные производные от перемещений;

· заданы комбинации напряжений и перемещений, записанные через нормальные и касательные производные от перемещений и через сами перемещения.

По известным перемещениям деформации определяются дифференцированием (симметричные соотношения Коши). Найденные по перемещениям деформации тождественно удовлетворяют шести уравнениям совместности деформаций По известным перемещениям можно найти дифференцированием компоненты тензора поворотов и псевдовектора поворотов (антисимметричные соотношения Коши). По известным деформациям напряжения определяются алгебраически (уравнения закона Гука).

2. Постановка задач теории упругости в напряжениях. Основные неизвестные — шесть компонент симметричного тензора напряжений. Они должны удовлетворять трем уравнениям равновесия, записанным в напряжениях, и шести уравнениям совместности деформаций, записанным с помощью уравнений закона Гука в напряжениях. Деформации определяются алгебраически по найденным напряжениям из обратных уравнений закона Гука. Перемещения интегрируются в квадратурах по найденным деформациям с помощью формул Чезаро, причем интегрируемость обеспечена, так как удовлетворены уравнения совместности деформаций. Для упрощения постановки напряжения можно выразить через тензорный потенциал так, что уравнения равновесия будут удовлетворяться тождественно, а уравнения совместности распадутся на отдельные уравнения для каждой из компонент тензора-потенциала напряжений. Удерживая те или иные компоненты симметричного тензора-потенциала напряжений, а остальные полагая нулю, можно получить как частные случаи известные постановки Максвелла, Моррера, Эри.

3. Постановка задач теории упругости в смешанном виде.

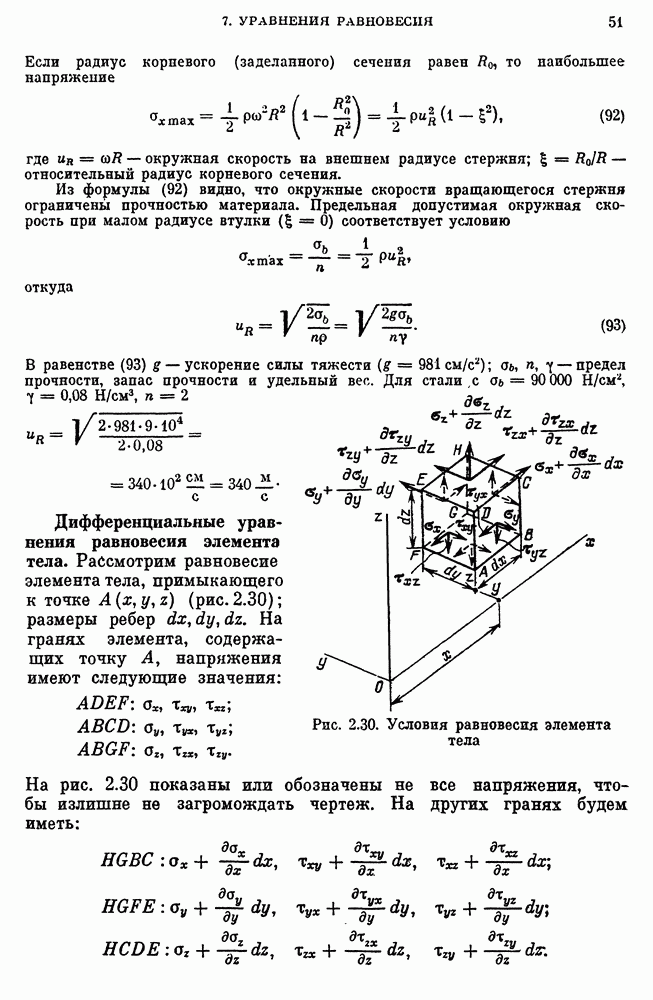
Фе́рма (фр. ferme, от лат. firmus прочный) — стержневая система в строительной механике, остающаяся геометрически неизменяемой после замены её жёстких узлов шарнирными. В элементах фермы, при отсутствии расцентровки стержней и внеузловой нагрузки, возникают только усилия растяжения-сжатия. Фермы образуются из прямолинейных стержней, соединенных в узлах^[1].

Ферма состоит из элементов: пояс, стойка, раскос, шпренгель (опорный раскос).

Дискретные системы (ДС) находят широкое применение в управ- лении разнообразными техническими устройствами, при этом основной составляющей ДС является микропроцессор. Область распространения ДС наиболее широкая – от простейших встроенных систем (например, музыкальные открытки, часы и т.п.), до сверхсложных комплексов управ- ления целыми системами и производствами. Основными причинами тако- го положения являются простота и экономичность построения аппаратной части, которая может выполнять алгоритмы высокой сложности по про- грамме, записанной в устройство. При этом модификация устройства с целью улучшения его характеристик зачастую происходит только заменой программного обеспечения, что открывает широкие просторы для по- строения универсальных микропроцессорных наборов для большого ко- личества объектов. ДС имеют ряд существенных преимуществ перед непрерывными системами, важнейшими из которых являются повышенная помехозащи- щённость и точность систем управления, ввиду того, что сигнал подвер- жен воздействию помех только в дискретные моменты времени. Благода- ря дискретному характеру информационных сигналов, можно эффективно использовать каналы передачи сигналов управления. Производители 4 электронных компонентов предлагают огромный выбор микропроцессор- ных устройств для построения ДС, а также инструментальные средства для разработки и отладки программного обеспечения. На современном рынке обычный человек может без проблем приобрести недорогой мик- роконтроллер, для которого существуют свободные инструментальные средства подготовки программного обеспечения, а также запрограммиро- вать его с помощью простейших программаторов, которые по силам со- брать даже неопытному в электронике радиолюбителю. Однако ДС имеют и некоторые недостатки, связанные, в первую очередь, с ограниченной предельной частотой работы управляющего уст- ройства и конечной разрядностью представления чисел в микропроцессо- ре. Ограниченная рабочая частота сужает круг областей применения ДС, а конечная разрядная сетка требует специальных математических приёмов для устранения накопления ошибок округления. Наличие импульсов вы- сокой частоты в ДС может значительно усложнить схемотехнику и ком- поновку устройства для достижения высокой степени электромагнитной совместимости и точности. Современная теория управления располагает универсальным ме- тодом исследования ДС, основанным на использовании математического аппарата – дискретного преобразования Лапласа (z-преобразование), ко- торый позволяет максимально приблизить методологию описания ДС к методологии описания непрерывных систем. Так, например, общими оп- ределениями являются передаточная функция, частотная характеристика и т.п. Однако эта аналогия в значительной степени носит лишь формаль- ный характер, вследствие чего теория управления ДС имеет существен- ные особенности, обусловленные наличием в этих системах импульсных элементов (ИЭ). В последнее время в области теории автоматического управления отмечается очень сильное развитие методов пространства состояний, кото- рые позволяют осуществить чёткую формализацию и механизацию вычис- лительных процедур для сложных и многомерных систем управления, где классические методы теории автоматического управления бессильны. К тому же синтез оптимального управления ориентирован на представле- нии модели системы в виде пространства состояний. Термин «пространство состояний» на самом деле является расширением давно проработанного математического аппарата матричных процедур решения различных задач в квантовой механике, аналитической динамике, при решении обыкновенных дифференциальных уравнений и др. Из преимуществ пространства состоя- ний можно выделить одинаковую формулировку различных зад