Численное решение задачи Коши для дифференциальных уравнений первого порядка

Пусть дано дифференциальное уравнение:

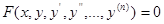(1).

Решением дифференциального уравнения (1) называется функция 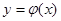, которая после её подстановки в уравнение превращает его в тождество.

Общее решение обыкновенного дифференциального уравнения n-го порядка содержит n произвольных постоянных 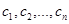, т. е. общее уравнение имеет вид .

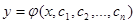Частное решение дифференциального уравнения получается из общего, если произвольным постоянным придать определенные значения.

Для выделения частного решения из общего нужно задавать столько дополнительных условий, сколько произвольных постоянных в общем решении, т.е. каков порядок уравнения.

В зависимости от способа задания дополнительных условий для получения частного решения дифференциального уравнения существует два типа задач: задача Коши и краевая задача. Если условия задаются в одной точке, то это задача Коши, если более чем в одной точке, то это краевая задача.

В математическом анализе разработано немало приемов нахождения решений дифференциальных уравнений через элементарные функции. Между тем весьма часто при решении практических задач эти методы либо неприменимы, либо их применение очень трудоемко. По этой причине для решения дифференциальных уравнений созданы приближенные методы. Самым распространенным приближенным способом решения дифференциальных уравнений является метод конечных разностей. Его сущность состоит в следующем: область непрерывного изменения аргумента заменяется дискретным множеством точек, называемых узлами. Эти узлы составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Эта функция называется сеточной. Исходное уравнение заменяется разностным уравнением относительно сеточной функции.

Такая замена называется аппроксимацией дифференциального уравнения на сетке. Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки.

Решение задачи Коши для дифференциального уравнения первого порядка 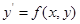, заключается в отыскании функции 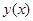, удовлетворяющей этому уравнению и начальным условиям 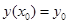, где 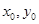- заданные числа.

Самые распространенные разностные методы решения поставленной задачи: метод Эйлера и метод Рунге – Кутта.