Решение. а). Подынтегральная функция имеет внутри контура интегрирования две особые точки и

а). Подынтегральная функция имеет внутри контура интегрирования две особые точк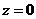и и 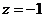. Тогда .

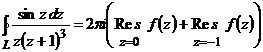Определим вид особых точек и найдем в них вычеты.

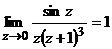, следовательно .

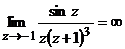, следовательно 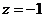- полюс.

Так как , то - полюс порядка .

.

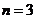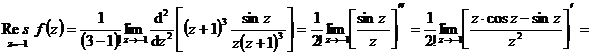
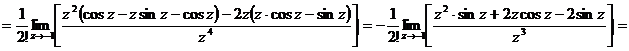
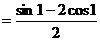Таким образом, .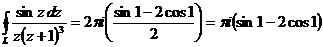

б). Подынтегральная функция имеет внутри контура интегрирования две особые точк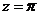и и 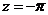. Тогда .

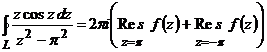Так как 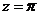и 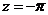- полюсы первого порядка, то для вычисления вычетов применим формулу 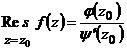, где , , .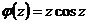

,

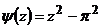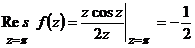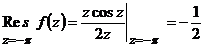
Таким образом, .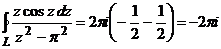

Задание 11. Вычислить интегралы с помощью вычетов.

а) ;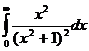

б) ;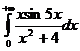

в) .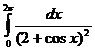

Решение.

а) Сформулируем правило, позволяющее вычислять несобственные интегралы от рациональной функции действительного переменного с помощью теории функций комплексного переменного:

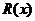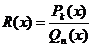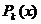Пусть - рациональная функция, , где и 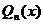- многочлены степен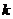и и 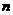соответственно. Если функция 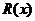непрерывна на всей действительной оси и 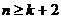, т.е. степень знаменателя по крайней мере на две единицы больше степени числителя, то

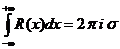
где 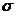означает сумму вычетов функции 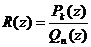по всем полюсам, расположенным в верхней полуплоскости.

Так как подынтегральная функция 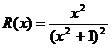четная, то 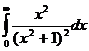= 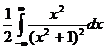. Построим функцию 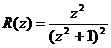, которая на действительной оси (при 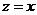) совпадает с подынтегральной функцией 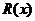. Особые точки функции 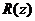- это точк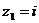и и 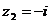. Из них в верхней полуплоскости находится точка 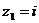, которая является полюсом второго порядка. Вычет функции 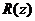относительно полюса 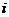равен = 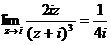. Так как в верхней полуплоскости только одна особая точка, то 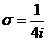. Следовательно, = .

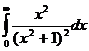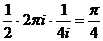б) Сформулируем правило, позволяющее вычислить рассматриваемый несобственный интеграл с помощью теории функций комплексного переменного:

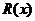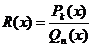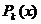Пусть - рациональная функция, , где и 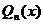- многочлены степен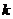и и 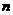соответственно. Если функция 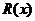непрерывна на всей действительной оси, 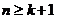, 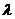- произвольное действительное число, то

;

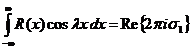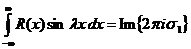
где 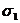означает сумму вычетов функции 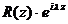по всем полюсам, расположенным в верхней полуплоскости.

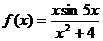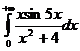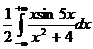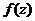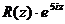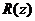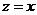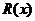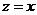Так как подынтегральная функция является четной, то = . Построим функцию = такую, что на действительной оси (при ) совпадает с : . Отметим, что при справедливо равенство 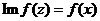. Функция 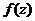имеет в верхней полуплоскости полюс первого порядка в точке 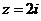. Вычет функции 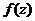относительно этого полюса равен 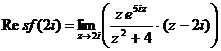= 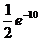. Следовательно, 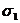= 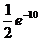и = .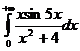

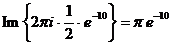в) Сформулируем правило, позволяющее вычислить определенный интеграл функции, зависящей рационально от тригонометрических функций с помощью теории функций комплексного переменного:

Пусть 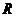- рациональная функция аргументов 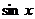и , и 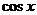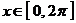функция 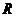непрерывна внутри промежутка интегрирования. Полагаем 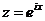, тогда 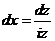, , 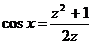, 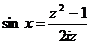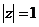. В этом случае

=

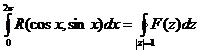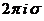
где 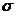есть сумма вычетов функции 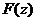относительно полюсов, заключенных внутри окружности .

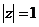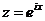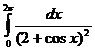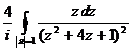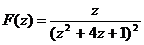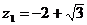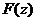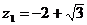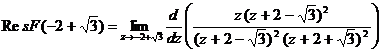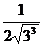В рассматриваемом интеграле применим подстановку и после преобразований получим: = . Внутри круга радиуса 1 с центром в начале координат содержится только одна особая точка подынтегральной функции - это точка , которая является полюсом второго порядка. Вычет функции относительно точки равен = . Следовательно, = .

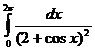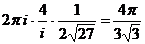Date: 2015-07-17; view: 1175; Нарушение авторских прав