Метод Эйлера-Лагранжа

Пример 3. Задано уравнение объекта в векторно-матричной форме:

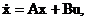
где 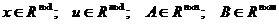, причем А и В зави­сят в общем случае от времени, в чем проявляется нестационар­ность объекта.

Критерий оптимальности - обобщенный квадратичный функционал:

.

Коэффициенты матриц Q и R также могут зависеть от време­ни по двум причинам:

- из-за нестационарности объекта;

- для того, чтобы в начальной стадии переходного процесса сделать критерий малочувствительным к величинам оши­бок, которые здесь определяются в основном начальными от­клонениями, а не свойствами оптимальной системы.

Требуется найти оптимальный алгоритм управления .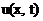

В результате решения получается оптимальный алгоритм с пропорциональным воздействием на объект по всем переменным состояния:

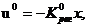
где

Матрица К в общем случае содержит зависящие от времени коэффициенты, которые находятся из системы нелинейных диф­ференциальных уравнений Риккати:

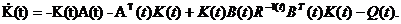
Если объект стационарный и функционал стационарный, то
коэффициенты регулятора от времени зависеть не будут. В част-
ности, для предыдущего примера Q = R = B = -А = 1, т. е. скаля-
ры, уравнение Риккати вырождается в квадратное уравнение

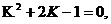которое имеет корень .

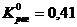Принцип оптимальности. Метод динамического программирования (МДП)

Непрерывная задача.

Пример 4. Задана система уравнений объекта:

,

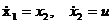и краевые условия: ,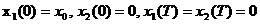

где Т – длительность оптимального процесса.

Задан критерий оптимальности, который необходимо миними­зировать:

,

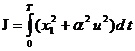где 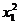характеризует качество процесса управления, а 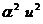- энергетические затраты на управление.

Ограничений на управление не наложено.

Требуется найти оптимальный алгоритм управления и°(х₁, х₂).

Решение.

1. Выбираем уравнение Беллмана для задачи Лагранжа, под­ставляя f ₀, f ₁ и f ₂:

.

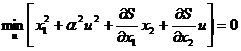2. Приравниваем к 0 производную по управлению и от мини-
мизируемой функции

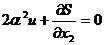
и находим отсюда оптимальное управление

.

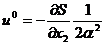3. Подставляем найденную функцию u⁰ в уравнение Беллмана и делаем преобразования, опуская знак минимума:

.

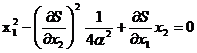4. Выбираем функцию Беллмана в виде квадратичной формы
с симметричной матрицей

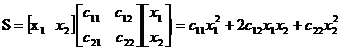
и, подставляя ее в уравнение Беллмана, получим

.

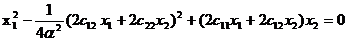Отсюда находим, приравнивая к 0 коэффициенты пр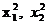и и :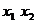

.

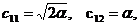
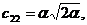
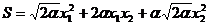5. Подставив последнее выражение в формулу для функции u ⁰, найдем оптимальное управление

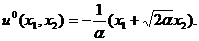
Соответствующая структурная схема оптимальной САУ (рис. 11) показывает, что оптимальным является регулятор с пропорциональным управлением по переменным состояния (ПД- регулятор).

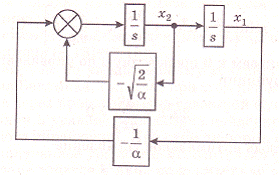
Рис. 11

Date: 2015-07-17; view: 622; Нарушение авторских прав