
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретико-множественное задание моделей. В самом общем случае (на концептуальнос уровне) модели изменения входного воздействия в виде функции пеpеxода и в виде функции выxода задаются в виде
В самом общем случае (на концептуальнос уровне) модели изменения входного воздействия в виде функции пеpеxода и в виде функции выxода задаются в виде соответствия.
Соответствие [12] ¾ это способ (закон) сопоставления элементов хÎХ с элементами yÎY так, что имеется возможность образования пар (двоек) (х,y), причем для каждого элемента хÎХ возможно указать элемент yÎY, с которым сопоставляется элемент х. В сопоставлении могут участвовать не все элементы Х и Y. Для задания соответствия необходимо указать:
- множество Х, элементы которого сопоставляются с элементами другого множества;
- множество Y, с элементами которого сопоставляются элементы множества Х;
- множество QÍХ´Y, определяющее закон, согласно которому осуществляется соответствие, т.е. перечисляющее все пары (х,y), участвующие в сопоставлении.
Соответствие, обозначаемое через q, представляет собой тройку множеств q = (Х, Y, Q), где Х ¾ область отправления соответствия, Y ¾ область прибытия соответствия, Q ¾ график соответствия, QÍХ´Y. Очевидно, что проекция Пр1QÍХ, а Пр2QÍY, причем множество Пр1Q называется областью определения соответствия, а проекция Пр2Q ¾ областью значений соответствия.
Модели динамичеcкой cиcтемы могут иметь вид функции и в этом случае говорят о существовании функционального отображения, как соответствия, для которого область определения Пр1Q совпадает с областью отправления Х. То есть для всякого хÎХ существует такой элемент yÎY, что двойка (х,y) Î Q.
Отображение q: X®Y называется функцией, если оно является однозначным, т.е. для любых пар (x1,y1)Î q и (x2,y2)Î q, если х1=х2, следует y1=y2.
Модели динамичеcкой cиcтемы могут быть также заданы в соответствии со способами задания соответствий.
При теоретико-множественном задании определяют множества Х={х1,х2,…,хn}, Y={y1,y2,…,ym} и график Q={(хi,yj)}, хÎХ, yÎY 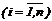 ,
, 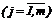 .
.
При матричном способе задания соответствие задается в виде матрицы инцидентности RQ, которая имеет вид прямоугольной таблицы размером n´m. Элементы хiÎХ соответствуют строкам матрицы RQ, а элементы yjÎY соответствуют столбцам. На пересечении хi строки и yj столбца ставится элемент rij=1, если элемент (хi,yj)ÎQ, и rij=0, если (хi,yj)ÏQ.
При графическом способе соответствие задается в виде рис. 1.5, на котором элементы хiÎХ ¾ кружки одной линии, элементы yjÎY ¾ кружки другой линии, а каждая двойка (хi,yj)ÎQ обозначается стрелкой, идущей от кружка хi к кружку yj. Такое представление называется графиком.

Х={х1,х2,х3,х4}, Y={y1,y2,y3},
Q={(х1,y1), (х1,y2), (х2,y1), (х2,y2), (х3,y2), (х4,y3)}
Рис. 1.5
Если сопоставлять элементы yÎY элементам множества Х, то получим соответствие q-1 =(Y,Х,Q-1), обратное соответствию q (инверсия соответствия q).
Исходя из приведенных выше определений множеств входных параметров Х=Х1´Х2´…´Хm, выходных параметров Y=Y1´Y2´…´Yr, состояний Z=Z1´Z2´…´Zn определим задание моделей функций переходов и выходов, как соответствий.
Если учитывается в определении состояния в текущий момент времени входной параметр и состояние в предшествующий момент времени, то модель системы в виде функции переходов будет задана соответствием
fП=(Х1´Х2´…´Хm, Z1´Z2´…´Zn, FП). (1.5)
Данная модель устанавливает соответствие fП между каждым векторным элементом X ={ х1,х2,…,хm }Î Х1´Х2´…´Хm и векторным элементом Z ={ z1,z2,…,zn }Î Z1´Z2´…´Zn; FП ¾ график соответствия fП.
Если учитывается в определении выходного параметра в текущий момент времени входной параметр и состояние или в предшествующий момент времени, или в текущий момент времени, то модель системы в виде функции выходов будет задана в виде соответствия
fВ ={[ (Х1´Х2´…´Хm), (Z1´Z2´…´Zn) ], (Y1´Y2´…´Yr), FВ }. (1.6)
Модель устанавливает соответствие fВ между каждым векторным элементом (Х,Z) из множества [(Х1´Х2´…´Хm), (Z1´Z2´…´Zn)] и векторым элементом Y ={ y1,y2,…,yr }Î Y1´Y2´ ´…´Yr. FВ – график соответствия fВ.
Если учитывается в определении выходного параметра в текущий момент времени входной параметр и состояние в предшествующий момент времени, а также в текущий момент времени, то модель системы в виде функции выходов может быть задана в виде:
fВ ={[(Х1´Х2´…´Хm)´(Z1´Z2´…´Zn)], [ Z1´Z2´…´Zn ],
(Y1´Y2´…´Yr), FВ), (1.7)
т.е. модель в данном случае устанавливает соответствие fВ между каждым векторным элементом {(X, Z), Z } из множества {[(Х1´Х2´…´Хm), (Z1´Z2´…´Zn)], [ Z1´Z2´…´Zn ]} и векторным элементом Y ={ y1,y2,…,yr }Î Y1´Y2´ ´…´Yr.
Можно применить более компактные записи моделей.
Модель системы в виде функции переходов может быть записана еще в следующем виде:
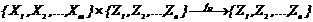 . (1.8)
. (1.8)
Модель системы в виде функции выходов может быть задана и в таком виде:
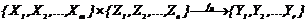 (1.9)
(1.9)
или в виде
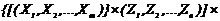
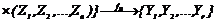 . (1.10)
. (1.10)
Date: 2015-07-17; view: 370; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |