
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

О. Критерий произведений
 eir: =
eir: = 
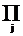 eij
eij
Правило выбора в этом случае формулируется так:
Матрица решений 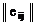 дополняется новым столбцом, содержащим произведения всех результатов каждой строки. Выбираются те варианты, в строках которых находятся наибольшие значения этого столбца.
дополняется новым столбцом, содержащим произведения всех результатов каждой строки. Выбираются те варианты, в строках которых находятся наибольшие значения этого столбца.
Применение этого критерия обусловлено следующими обстоятельствами:
1) вероятности появления состояния Fj неизвестны;
2) с появлением каждого из состояний Fj по отдельности необходимо считаться;
3) критерий применим и при малом числе реализаций решения;
4) некоторый риск допускается.
Критерий произведений приспособлен в первую очередь для случаев, когда все eij положительны. Если условие положительности нарушается, то следует выполнять некоторый сдвиг eij + а с некоторой константой а > ï  eij ï. Результат при этом будет, естественно зависеть от а. На практике чаще всего
eij ï. Результат при этом будет, естественно зависеть от а. На практике чаще всего
а:= ï  eij ï +1.
eij ï +1.
Если же никакая константа не может быть признана имеющей смысл, то критерий произведений не применим.
5о. Пример.
Рассмотрим тот же пример (табл. 1).
Построение оптимального решения для матрицы решений о проверках по критерию Гурвица имеет вид (при С =0.5, в 103):
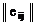
| С 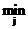 eij eij
| (1-С) 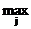 eij eij
| eir |  eir eir
| ||
| -20.0 | -22.0 | -25.0 | -12.5 | -10.0 | -22.5 | |
| -14.0 | -23.0 | -31.0 | -15.5 | -7.0 | -22.5 | |
| -24.0 | -40.0 | -20.0 | -20.0 | -20.0 |
В данном примере у решения имеется поворотная точка относительно весового множителя С: до С = 0.57 в качестве оптимального выбирается Е3, а при больших значениях – Е1.
Применение критерия Ходжа-Лемана (q = 0.33, n = 0.5, в 103):
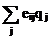
| 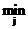 eij eij
| n 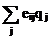
| (1-n) 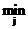 eij eij
| eir |  eir eir
|
| -22.33 | -25.0 | -11.17 | -12.5 | -23.67 | -23.67 |
| -22.67 | -31.0 | -11.34 | -15.5 | -26.84 | |
| -21.33 | -40.0 | -10.67 | -20.0 | -30.76 |
Критерий Ходжа-Лемана рекомендует вариант Е1 (полная проверка) – так же как и ММ-критерий. Смена рекомендуемого варианта происходит только при n = 0.94. Поэтому равномерное распределение состояний рассматриваемой машины должно распознаваться с очень высокой вероятностью, чтобы его можно было выбрать по большему математическому ожиданию. При этом число реализаций решения всегда остаётся произвольным.
Критерий Гермейера при qj = 0.33 даёт следующий результат (в 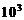 ):
):
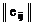
| 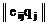
| eir = 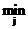 eijqj eijqj
|  eir eir
| ||||
| -20.0 | -22.0 | -25.0 | -6.67 | -7.33 | -8.33 | -8.33 | -8.33 |
| -14.0 | -23.0 | -31.0 | -4.67 | -7.67 | -10.33 | -10.33 | |
| -24.0 | -40.0 | -8.0 | -13.33 | -13.33 |
В качестве оптимального выбирается вариант Е1. Сравнение вариантов с помощью величин eir показывает, что способ действия критерия Гермейера является даже более гибким, чем у ММ-критерия.
В таблице, приведенной ниже, решение выбирается в соответствии с BL(MM)-критерием при q1=q2=q3 =1/2 (данные в 103).
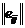
| 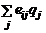
| 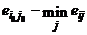
| 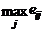
| 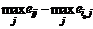
| ||
| -20.0 | -22.0 | -25.0 | -23.33 | -20.0 | ||
| -14.0 | -23.0 | -31.0 | -22.67 | +6.0 | -14.0 | +6.0 |
| -24.0 | -40.0 | -21.33 | +15.0 | +20.0 |
Вариант Е3 (отказ от проверки) принимается этим критерием только тогда, когда риск приближается к  . В противном случае оптимальным оказывается Е1. Во многих технических и хозяйственных задачах допустимый риск бывает намного ниже, составляя обычно только незначительный процент от общих затрат. В подобных случаях бывает особенно ценно, если неточное значение распределения вероятностей сказывается не очень сильно. Если при этом оказывается невозможным установить допустимый риск
. В противном случае оптимальным оказывается Е1. Во многих технических и хозяйственных задачах допустимый риск бывает намного ниже, составляя обычно только незначительный процент от общих затрат. В подобных случаях бывает особенно ценно, если неточное значение распределения вероятностей сказывается не очень сильно. Если при этом оказывается невозможным установить допустимый риск 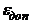 заранее, не зависимо от принимаемого решения, то помочь может вычисление ожидаемого риска
заранее, не зависимо от принимаемого решения, то помочь может вычисление ожидаемого риска 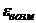 . Тогда становится возможным подумать, оправдан ли подобный риск. Такое исследование обычно дается легче.
. Тогда становится возможным подумать, оправдан ли подобный риск. Такое исследование обычно дается легче.
Результаты применения критерия произведения при а = 41×103 и а = 200×103 имеют вид:

| eir =  eij eij
|  eir eir
| |||
| +21 | +19 | +16 | |||
| а =41 | +27 | +18 | +10 | ||
| +41 | +17 | +1 | |||
| +180 | +178 | +175 | |||
| а =200 | +186 | +177 | +169 | ||
| +200 | +176 | +160 |
Условие eij > 0 для данной матрицы не выполнимо. Поэтому к элементам матрицы добавляется (по внешнему произволу) сначала а = 41×103, а затем а = 200×103.
Для а = 41×103 оптимальным оказывается вариант Е1, а для а = 200×103 – вариант Е3, так что зависимость оптимального варианта от а очевидна.
Лекция 11
Часть 2. Теория игр.
КЛАССИФИКАЦИЯ ИГР.
Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д.
В зависимости от количества игроков различают игры двух и n игроков. Первые из них наиболее изучены. Игры трёх и более игроков менее исследованы из-за возникающих принципиальных трудностей и технических возможностей получения решения. Чем больше игроков - тем больше проблем.
По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий игра называется бесконечной.
По характеру взаимодействия игры делятся на:
1) бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции;
2) коалиционные (кооперативные) – могут вступать в коалиции.
В кооперативных играх коалиции наперёд определены.
По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.
По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др.
Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 2, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).
Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования.
Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)
Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные.
Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения.
Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определённого числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.
Date: 2015-07-17; view: 726; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |