б) Потенциал. Поскольку работа при перемещении заряда в потенциальном поле не зависит от траектории, а зависит лишь от начальной и конечной точек пути

Поскольку работа при перемещении заряда в потенциальном поле не зависит от траектории, а зависит лишь от начальной и конечной точек пути, ее можно выразить через координаты концов траектории. Это делается с помощью потенциала. Если пробный заряд перемещается между точками 1 и 2, то работа равна:

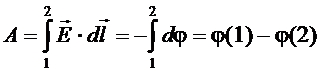. (1.32)

Здесь 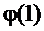и 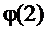- значения потенциала в точках 1 и 2. Определенная таким образом величина называется потенциалом поля. Ясно, что потенциал – это величина, численно равная потенциальной энергии положительного единичного (пробного) заряда в данной точке поля. Верно также, что разность потенциалов 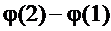между двумя точками электростатического поля равна взятой с обратным знаком работе, совершаемой при перемещении пробного заряда из точки 1 в точку 2.

Установим связь между потенциалом и напряженностью электростатического поля 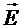. Так как:

,

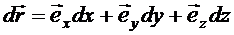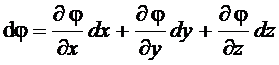, (1.33)

то, определив градиент потенциала как:

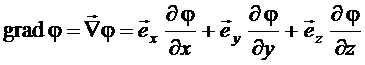, (1.34)

получим из (1.33):

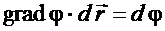(1.35)

или

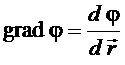. (1.36)

Из (1.35) ясно, что бесконечно малое приращение потенциала 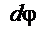при перемещении в некотором направлении равно компоненте потенциала по этому направлению, умноженной на величину перемещения. Сравнивая (1.36) с (1.32), можно записать:

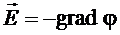(1.37)

или 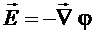, (1.38)

т.е. напряженность поля равна градиенту потенциала с обратным знаком.

Введем понятие эквипотенциальной поверхности как поверхности, во всех точках которой потенциал имеет одно и то же значение. Изобразим поверхности 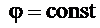: 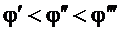(рис.1.16).

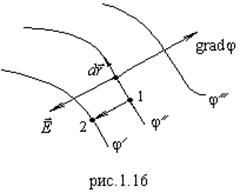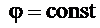
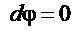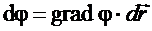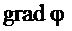При перемещении вдоль . Так как , то . Значит, вектор направлен перпендикулярно эквипо-тенциальной поверхности, 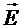противоположен .

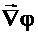Разность потенциалов - это работа по перемещению пробного заряда из точки 1 в точку 2 (см.рис.1.16) – из точки, отвечающей большему потенциалу, в точку, отвечающую меньшему потенциалу.

Если это перемещение совершается вдоль 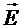, т.е. 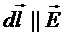, тогда .

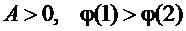Найдем потенциал поля точечного заряда. Считая, что в формуле

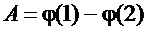
точка 2 находится на бесконечности, полагаем 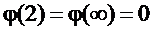. Тогда

.

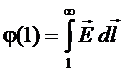Поле точечного заряда сферически симметрично, поэтому путь интегрирования возьмем по радиус-вектору .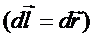

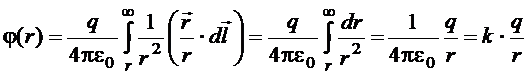. (1.39)

По принципу суперпозиции для потенциала системы точечных зарядов

.

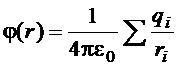При непрерывном распределении заряда

. (1.40)

Единица измерения потенциала – Вольт (В).

Примеры.

1. Электрический диполь – это система из двух одинаковых по модулю, но разноименных точечных зарядов, находящихся на расстоянии 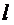друг от друга.

Найти потенциал и напряженность поля диполя (рис.1.17).

Введем электрический момент диполя, направленный от 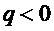к :

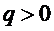. (1.41)

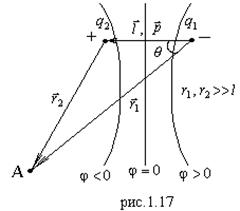Потенциал для диполя в точке А:

:

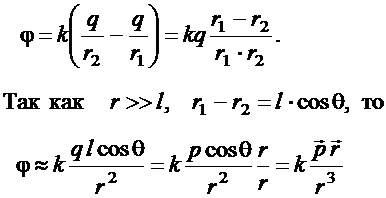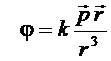. (1.42)

Из формулы (1.42) видно, что потенциал диполя зависит от электрического момента 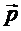. Найдем напряженность поля 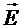диполя:

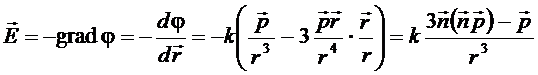, (1.43)

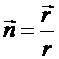. При 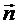, сонаправленном с 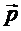, получим:

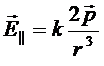- напряженность поля на оси диполя.

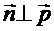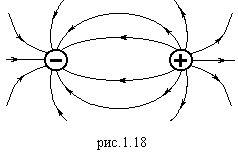
При : 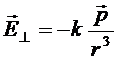, напряженность поля перпендикулярно оси диполя. Силовые линии вблизи диполя показаны на рис.1.18.

Модуль вектора :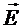

.

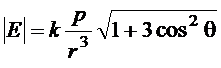2. Найти потенциал шара, равномерно заряженного по объему зарядом q.

Напряженность поля шара была найдена ранее в § 1.4. Найдем потенциал в центре шара по формуле (1.40):

. (1.44)

При этом, 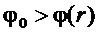. Для нахождения 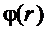воспользуемся формулой, связывающей напряженность поля и потенциал:

.

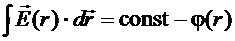Учтем, что 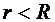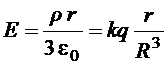при: ; при 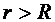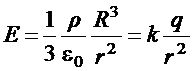(см.(1.24) и (1.25)). Тогда:

;

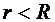
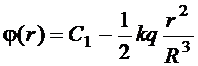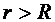
, – учтено, что .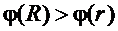

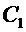найдем из граничного условия для , .

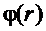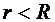При 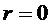; 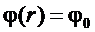. Тогда:

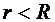
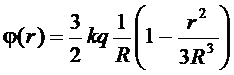. (1.45)

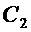найдем из следующего граничного условия: пр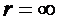и и 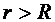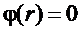, т.е. 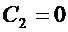. Тогда

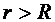
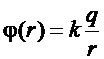. (1.46)

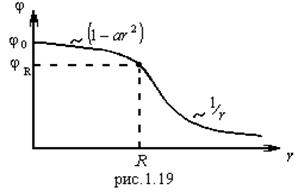График зависимости показан на рис.1.19. Видно, что потенциал 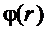непрерывно уменьшается от 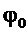до 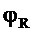внутри шара и от 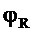до нуля снаружи.

Date: 2015-07-17; view: 601; Нарушение авторских прав