Бегущие волны в открытых системах

Часть 2. Волны

5.1 Распространение волн

В настоящем разделе рассматривается распростране-ние колебаний в открытых системах, т.е. системах, не имеющих внешних границ. Колебания распространяются в виде волн.

Волнами называются процесс распространения возму-щений в пространстве, т.е. волна – это процесс распрост-ранения колебаний от одной точки пространства к дру-гой. Характерной особенностью волн является перенос энергии и импульса без переноса вещества. Основными видами волн являются упругие волны, распространяю-щиеся в упругих средах, волны, возникающие на границе раздела подвижных сред, и электромагнитные волны. Для упругих волн, то есть волн, распространяющихся в упругой среде характерно, что распространяется только возмущение среды, сами же частицы среды колеблются относительно среднего положения. Упругие волны возни-кают в случае, когда при деформации среды возникают упругие силы, противодействующие деформации. Волны на границе раздела возникают как по причине распростра-нения первоначального возмущения (волны, разбегающи-еся от брошенного камня, цунами), так и по причине тан-генциального разрыва вектора скорости при движении одной среды относительно другой (волны, возникающие из-за ветра, дующего над поверхностью воды). Электро-магнитные волны – процесс распространения в простран-стве поперечных колебаний электрического и магнитного полей. К электромагнитным волнам относятся, в частнос-ти, световые и радиоволны.

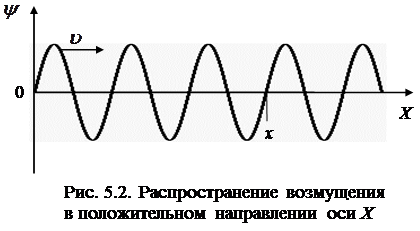
Волны по форме испускания подразделяются на нес-колько видов. Импульсом или одиночной волной называют короткое возмущение, не имеющее регулярного харак-тера. Цугом волн называется ограниченное число повто-ряющихся возмущений, то есть небольшое количество гармонических возмущений. Гармонической волной на-зывается бесконечная синусоидальная волна, в которой изменение возмущения среды происходит по закону си-нуса или косинуса (рис. 5.1).

Под возмущением среды обычно понимают смещение частиц среды относительно положения равновесия. Здесь под обозначением 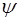и понимается возмущение среды, т. е., смещение частиц среды. Заметим, что в общем случае ме-рой возмущения может быть не только смещение частиц среды. Возмущение может выражаться и через изменение давления, как в звуковых волнах, и через изменение дру-гих характеристик среды.

Однако, в большинстве случаев для упругих волн в ка-честве меры возмущения обычно применяют смешение частиц среды.

В зависимости от направления колебания частиц среды различают волны продольные и поперечные. В попереч-ных волнах частицы колеблются в направлении, перпен-дикулярном направлению распространения волны. В про-дольных волнах частицы колеблются в направлении рас-пространения волны. Упругие поперечные волны могут воз-никнуть лишь в среде, обладающей сопротивлением сдви-гу, поэтому в жидкой и газообразний среде возможно воз-никновение только продольных волн. В твердой среде воз-можно возникновение и продольных и поперечных волн.

Иллюстрацией к сказанному для поперечных волн мо-жет служить рис. 5.1. Тогда на нём буква 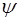означает сме-щение частиц в направлении, перпендикулярном оси X, являющейся направлением распространения волны. Тот же рис. 5.1 может служить иллюстрацией продольных волн, распространяющихся вдоль оси X, только тогда под буквой 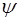надо понимать смещение частиц среды в на-правлении самой оси X.

Фронтом волны называется геометрическое место то-чек, до которых доходит возмущение в момент времени . Волновой фронт представляет собой поверхность, отделя-ющую часть пространства, в котором колебания уже воз-никли от той части, где волновой процесс еще не начал-ся. Волновой поверхностью называется геометрическое место точек, колеблющихся в одной фазе. Волновых по-верхностей может быть бесконечно много (зависит от выбора фазы), они остаются неподвижными; волновой же фронт один и он постоянно перемещается. В зависимости от формы волновой поверхности различают несколько простейших видов волн: плоская, сферическая, цилиндри-ческая. Конечно, существует большое количество волн и более сложной формы.

Несмотря на большое разнообразие волновых процес-сов, их образование происходит по общему принципу. Возмущение, произошедшее в точке А среды, через оп-ределенное время проявляется на интересующем нас рас-стоянии от точки А, то есть передается с определенной скоростью.

5.2 Уравнение волны

Начнём рассмотрение волн с самого простого случая гармонических волн, возникающих при распространении колебаний, испущенных источником, колеблющимся по закону синуса или косинуса.

Получим уравнение, описывающее распространение вол-ны от точечного источника в среде, не поглощающей энер-гию.

Пусть в точке x= 0 находится источник возмущения 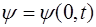. Возмущение распространяется в положитель-ном направлении оси X со скоростью 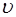(рис. 5.2)

Для того, чтобы возмущение достигло точки x, ему по-надобится некоторое время, равное:

(5.1)

Иначе говоря, возмущение в любой точке x будет за-паздывать по времени от возмущения в точке x=0 на ве-личину времени, описанную уравнением (5.1). Тогда, что-бы описать возмущение в любой точке x, нам необходимо учесть это запаздывание. Функция, описывающая возму-щение, достигшее точки x с запаздыванием , принимает вид:

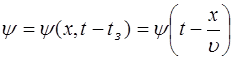. (5.2)

Итак, функция, описывающая возмущение, распростра-няющееся в положительном направлении оси X, должна быть функцией от координаты и времени, причём аргу-менты функции должны иметь структуру .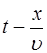

Пусть в точке x= 0 находится источник гармонических колебаний:

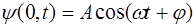, (5.3)

где 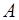– амплитуда колебания;

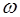– его частота;

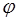– начальная фаза;

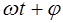– фаза колебания.

Тогда колебание из точки 0 придет с запаздыванием, описанным выражением (5.1). Выражение, описывающее колебание в любой точке x, принимает вид:

. (5.4)

Полученное выражение называется уравнением гармо-нической волны, распространяющейся в положительном направлении оси x.

Нетрудно видеть, что волна, распространяющаяся в от-рицательном направлении оси x, будет описываться урав-нением:

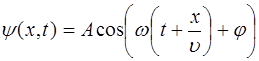. (5.5)

Уравнениям (5.4) и (5.5) можно придать вид, симмет-ричный относительно времени и координаты. Такой вид более наглядно представляет свойства волн. Внесем в вы-ражении (5.4) частоту 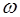в скобки:

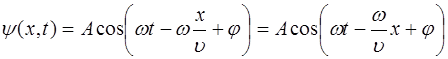. (5.6)

Введя обозначение:

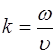, (5.7)

получим уравнение гармонической волны в симметричном виде:

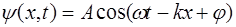. (5.8)

Число k называется волновым числом. Уравнения вол-ны (5.4) и (5.8) выводились в предположении, что среда, в которой происходит распространение волны, не погло-щает энергию, т.е. амплитуда колебаний частиц среды A постоянна. В том случае, когда распространение волны происходит в однородной среде с поглощением, ампли-туда уменьшается по экспоненциальному закону в зави-симости от расстояния x, которое волна прошла от своего источника:

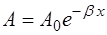, (5.9)

где z – координата рассматриваемой точки;

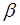– линейный коэффициент поглощения;

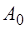– амплитуда в точке x= 0.

Тогда уравнение волны, распространяющейся в погло-щающей среде, принимает вид:

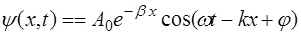. (5.10)

5.3 Характеристики волны

Рассмотрим свойства волны, описанной уравнением (5.8). Зафиксируем координату x. В этом случае уравне-ние (5.8) описывает гармоническое колебание точки, при-чем периодичность составляет 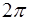. Найдем промежуток времени 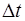, через которое колебание в точности повто-ряется. Из периодичности косинуса 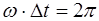находим:

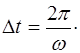(5.11)

Этот промежуток времени называется периодом коле-баний:

(5.12)

Итак, волна периодична во времени.

Теперь зафиксируем время t. Тогда становится видно, что волна периодична в пространстве, причем периодич-ность такая же, что и во времени: 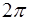. Найдем соответ-ствующее расстояние 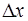. Из периодичности в простран-стве находим:

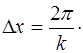(5.13)

Расстояние 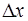называется длиной волны :

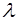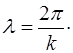(5.14)

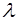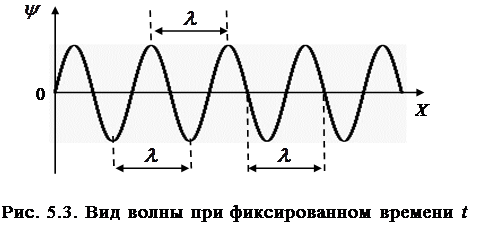
Таким образом, длина волны – это расстояние меж-ду ближайшими точками среды, колеблющимися с разно-стью фаз 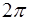. Рассмотрев «моментальный снимок» вол-ны, представленный на рис. 5.3, можно видеть, что длина волны – это также расстояние между соседними макси-мумами (или минимумами) волны.

Длина волны имеет ещё один физический смысл. Для выяснения его подставим в выражение (5.14) определение волнового числа (5.7). Получим:

. (5.15)

Итак, длина волны 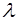– это расстояние, на которое волна распространяется со скоростью 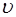за время, рав-ное периоду колебаний .

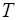С учетов выражений (5.12) и (5.14) запишем ещё одно уравнение волны, наглядно отражающее свойства волны. Из (5.12) имеем:

, (5.16)

а из (5.14) получаем:

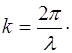(5.17)

Подставим (5.16) и (5.17) в уравнение волны (5.8) и для простоты выберем начало отсчета по оси X так, что-бы начальная фаза 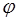была равна нулю. Это никак не отразится на общности рассуждений и выводов, но сэко-номит труд при записи выражений. Получим:

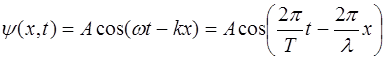. (5.18)

Вынося за скобки 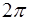, получаем окончательно:

. (5.19)

Выясним физический смысл скорости 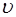распростране-ния волны. Зафиксируем определенную фазу волны:

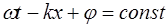, (5.20)

и продифференцируем выражение для фазы по времени. Получим:

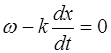, (5.21)

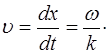(5.22)

Из (5.22) видно, что под скоростью распространения волны понимается фазовая скорость 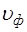, то есть ско-рость распространения определенной фазы волны:

(5.23)

5.4 Примеры волн

5.4.1 Уравнение плоской волны

В плоской волне волновые поверхности имеют вид плос-костей. Если плоская волна распространяется вдоль од-ной из осей, например, вдоль оси X, то волновые повер-хности перпендикулярны и направлению распростране-ния, и оси, вдоль которой происходит распространение. Такая волна описывается полученным ранее уравнением (5.8). Таким образом, уравнение (5.8) представляет собой частный случай уравнения плоской волны. Получим об-щее уравнение.

Рассмотрим плоскую волну, распространяющуюся в произвольном направлении, характеризуемом единичным вектором нормали 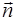к волновой поверхности (рис. 5.4):

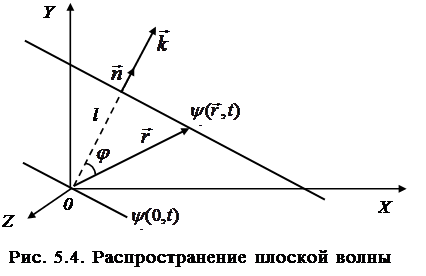Рассмотрим две волновые поверхности. Одна, 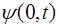, в момент времени t проходит через начало координат. Вто-рая поверхность, 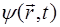, параллельная первой, отстоит от нее на расстояние l и ее точки могут быть определены ра-диусом .

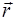Определим расстояние 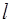от начала отсчета до плоскос-ти 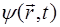. Оно может быть выражено как скалярное про-изведе-ние вектора 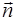нормали к волновой плоскости на радиус-вектор 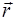любой точки плоскости :

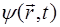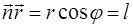. (5.24)

Колебания в плоскости 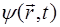будут отставать от коле-баний в плоскости 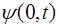, проходящей через начало от-счета на время:

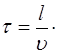(5.25)

Тогда, если колебания в плоскости, проходящей через начало отсчета имеют вид 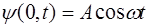, то в рассматри-ваемой плоскости 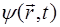колебания вид будет следующий:

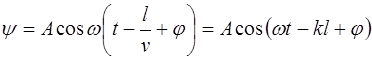. (5.26)

Заменим, согласно (5.24), 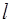на . Получим:

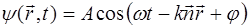. (5.27)

Полученное выражение (5.27) описывает гармоничес-кие колебания частицы относительно положения равнове-сия, возникающие при прохождении гармонической вол-ны. Положение равновесия частицы определяется радиу-сом-вектором .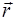

Для определения направления распространения волны введём понятие волнового вектора. Волновой вектор равен по модулю волновому числу и совпадает по нап-равлению с вектором нормали к волновой плоскости :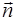

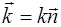. (5.28)

С учетом уравнений (5.7) и (5.17), определяющих зави-симость волнового числа от циклической частоты 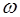, фа-зовой скорости волны 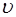и длины волны 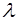, получим выра-жение для волнового вектора:

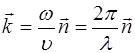. (5.29)

Подставив в (5.27) выражение для волнового вектора (5.28), получим уравнение плоской волны, распростра-няющейся в направлении, определяемом волновым векто-ром :

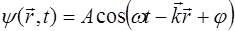. (5.30)

В случае распространения волны в среде, поглоща-ющей энергию, амплитуда волны уменьшается по экспо-ненциальному закону (см. выражение (5.9)). В этом слу-чае уравнение плоской волны принимает вид:

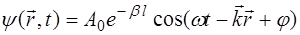, (5.31)

или, согласно (5.24),

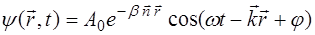. (5.32)

Перейдем к описанию плоской волны в проекциях на координатные оси 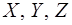. При распространении плоской волна в пространстве, вектор 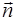нормали к волновой по-верхности (и, соответственно, сонаправленный ему волно-вой вектор ) образует углы с осями координат 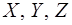углы 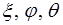. Тогда волновой вектор может быть вы-ражен как:

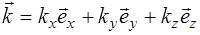, (5.33)

а радиус-вектор как:

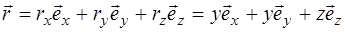. (5.34)

Здесь 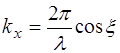– проекция вектора на ось X;

– проекция вектора на ось Y;

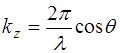– проекция вектора на ось Z;

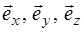– орты осей 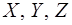соответственно.

Тогда скалярное произведение 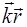можно выразить через проекции векторов на координатные оси:

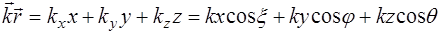. (5.35)

С учетом этого уравнение плоской волны (5.30) в трех-мерном случае примет вид:

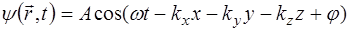. (5.36)

Расположив одну из координатных осей, например X, в направлении распространения плоской волны мы полу-чим, что проекции волнового вектора 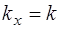; ; ; 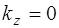положение колеблющейся точки будет описываться толь-ко координатой x, и тогда уравнение (5.36) перейдет в уравнение (5.8). Таким образом, как уже было отмечено, уравнение (5.8) описывает также и плоскую волну, рас-пространяющуюся в положительном направлении оси X.

5.4.2 Уравнение сферической волны

В сферической волне волновые поверхности (и волно-вой фронт) имеют вид сфер с центром в источнике волны (рис. 5.5).

В действительности любой источник имеет некоторые размеры, соответственно волновые поверхности на неболь-ших расстояниях от источника имеют вид более сложный, чем сфера. Но на расстояниях, значительно превышаю-щих размеры источника, последний может считаться то-чечным, и форма волновых поверхностей очень близка к сферической.

Получим уравнение, описывающее распространение сфе-рической волны. Совместив начало отсчета с источником, увидим, что колебания точки, определяемой радиусом-вектором 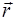, и находящейся на расстоянии 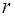от источ-ника, определится выражением:

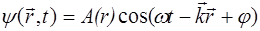, (5.37)

где – амплитуда колебания точки, находящейся на рас-стоянии 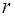от источника.

Определим зависимость амплитуды волны от расстоя-ния до источника. Энергия колебаний пропорциональна квадрату амплитуды (при постоянстве прочих параметров колебательной системы):

. (5.37)

Если волна распространяется в среде, не поглощающей энергию, то через любую сферическую поверхность ради-усом 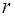и площадью 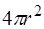проходит одинаковое количество энергии всей волны, равной энергии волны, испущенной источником, т.е. имеет место зависимость:

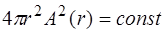, (5.38)

откуда видна зависимость амплитуды колебаний точки от расстояния до источника:

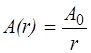, (5.39)

где 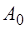– постоянная величина, равная амплитуде на еди-ничном расстоянии от источника.

Таким образом, уравнение сферической волны прини-мает вид:

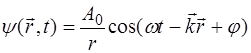. (5.40)

Колебания частиц при прохождении сферической вол-ны зависят только от расстояния до источника, и поэтому выражение (5.40) можно записать в скалярном виде:

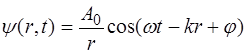, (5.41)

где 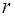– растояние от источника.

Date: 2015-06-11; view: 744; Нарушение авторских прав