
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод наименьших квадратов
Как же определить эти неизвестные коэффициенты? По-видимому, первое, что должно прийти в голову: рассмотреть интеграл от функции невязки:
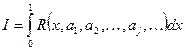 (21)
(21)
Поскольку функции  в приближенном решении (17) являются заданными функциями, то интеграл (21) легко вычисляется и представляет собой функцию неизвестных параметров
в приближенном решении (17) являются заданными функциями, то интеграл (21) легко вычисляется и представляет собой функцию неизвестных параметров  . Условие минимума этой функции:
. Условие минимума этой функции:
 (22)
(22)
образует систему, в которой количество уравнений равно количеству неизвестных  .
.
 |
Однако, возможна ситуация, показанная на рис.7а, когда интеграл от невязки мал, или даже равен нулю, но отличие функции невязки от нуля может быть большим.
Другой возможный подход: вычислять интеграл не от функции невязок, а от ее модуля:
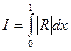 . (23)
. (23)
Этот подход устраняет рассмотренную выше опасность, однако (см рис.7б) возможна ситуация, когда невязка, принимая небольшие значения на большей части интервала, оказывается большой на малой его части. В этом случае малое значение интеграла (21) вовсе не гарантирует высокую точность приближенного решения.
Постепенно мы пришли к идее первого из широко используемых на практике методов построения приближенного решения в виде аппроксимации системой функций: метода наименьших квадратов. В этом методе минимизируется интеграл от квадрата невязки:
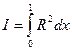 (24)
(24)
В этом случае, устраняется опасность, представленная на рис.6а, и снижается, хотя и не устраняется совсем вторая опасность (рис.6б)
Рассмотрим применение этого метода на примере задачи (1). Для этой задачи  и, следовательно
и, следовательно
 (25)
(25)
Из условий минимума
 (26)
(26)
Получаем систему линейных уравнений:
 (27)
(27)
Здесь  ‑ матрица,
‑ матрица,  ,
,  ‑ векторы. Размер системы равен количеству неизвестных коэффициентов
‑ векторы. Размер системы равен количеству неизвестных коэффициентов  , то есть количеству аппроксимирующих функций, принятых для приближенного представления решения (17).
, то есть количеству аппроксимирующих функций, принятых для приближенного представления решения (17).
Для аппроксимации во всех примерах будет использоваться система функций (18):  . Поскольку
. Поскольку

для матрицы  и вектора
и вектора  получаем
получаем

и решение этой системы дает значения коэффициентов (17):

Подставляя эти значения в (17), получаем выражение для вычисления приближенного решения при любом значении  .
.
Дополним таблицу 1 столбцом значений для полученного приближенного решения.
Таблица 2
| x | Точное решение | МКР | Метод наименьших квадратов |
| 0.25 | -0.0716449 | -0.0754442 | -0.0717608 |
| 0.5 | -0.1013212 | -0.1066942 | -0.1010489 |
| 0.75 | -0.0716449 | -0.0754442 | -0.0717608 |
Сравнивая полученные результаты с результатами, полученными по методу конечных разностей, можно отметить их более высокую точность. Однако за это пришлось заплатить несколько большей трудоемкостью при построении разрешающей системы.
На рис.8 приведены графики точного (1) и приближенного (2) решений. Если бы эти графики привести в том же масштабе, что и на рис.5, они слились бы в одну линии. Поэтому на рис.8 в сильно увеличенном масштабе показаны решения для небольшой области, где разница между приближенным и точным решением максимальна.

Рис.8
Date: 2016-08-31; view: 400; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |