Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Преобразование неограниченных по знаку переменных

⇐ ПредыдущаяСтр 39 из 66Следующая ⇒




 

Переменные, принимающие как положительные, так и отрицательные значения, следует заменять разностью двух неотрицательных:

x = x+ - x-; x+ ³ 0; x- ³ 0.

Приведем к стандартной форме следующую задачу ЛП:

W = x1 - 2 x2 + 3 x3 ® max;

x1 + x2 + x3 £ 8;

x1 - x2 + x3 ³ 9;

3 x1 - x2 - 2 x3 = -17;

x1 ³ 0; x2 ³ 0,

где x3 - переменная, неограниченная по знаку.

 

Последовательность действий следующая:

1. Умножим обе части равенства на -1, так как все элементы матрицы ресурсов должны быть неотрицательными.

2. Заменим x3 на x4-x5, где x4 и x5 ³ 0.

3. Введем дополнительные остаточную x6 и избыточную x7 переменные в два первых неравенства.

4. Припишем нулевые значения оценок задачи ЛП при переменных x6 и x7. Значение целевой функции при этом не изменится.

После преобразований имеем стандартную форму задачи ЛП:

W = x1 - 2 x2 + 3 x4 - 3 x5 ® max;

x1 + x2 + x4 - x5 + x6 = 8;

x1 - x2 + x4 - x5 - x7 = 9;

-3 x1 + x2 + 2 x4 - 2 x5 = 17;

x1 ³ 0; x2 ³ 0; x4 ³ 0; x5 ³ 0; x6 ³ 0; x7 ³ 0.

2.4. Основы симплекс - метода линейного программирования

 

Симплекс - метод представляет собой итеративную процедуру решения задач ЛП, записанную в стандартной форме. Система уравнений, характеризующая набор условий приводится к каноническому виду с помощью элементарных операций над матрицами:

x1 + a 1,m+1×xm+1 +... + a 1s×xs+...+ a 1n×xn = b 1;

...

x2 + a 2,m+1×xm+1 +... + a 2s×xs+...+ a 2n×xn = b 2;

...

xm + a m,m+1×xm+1 +... + a ms×xs+...+ a mn×xn = b m.

Переменные x1, x2,...,xm, входящие с единичными коэффициентами только в одно уравнение системы и с нулевыми - в остальные, называются базисными. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Остальные n-m переменных (xm+1,...,xn) называются небазисными переменными.

Для приведения системы к каноническому виду можно использовать два типа элементарных операций над строками:

1. Умножение любого уравнения системы на положительное или отрицательное число.

2. Прибавление к любому уравнению другого уравнения системы, умноженного на положительное или отрицательное число.

 

Алгоритм симплекс - метода:

1. Выбираем начальное допустимое базисное решение. Базисным решением называется решение, полученное при нулевых значениях небазисных переменных, т.е. xi=0, i=m+1,...,n. Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных неотрицательны, т.е. xj = b j ³ 0, j=1,2,...,m. В этом случае целевая функция примет следующий вид: W = c b× x b = c1× b1 + c2× b 2+...+cm×bm. Заполняем первоначальную таблицу симплекс - метода:

Таблица 9.3

cb xb c1 C2 ... cm cm+1 ... cn b i
  базис x1 X2 ... xm xm+1 ... xn  
с1 x1     ...   a 1,m+1 ... a1 n b1
с2 x2     ...   a 2,m+1 ... a2 n b2
... ... ... ... ... ... ... ... ... ...
cm xm     ...   a m,m+1 ... am n b m
                  W

 

2. Вычисляем вектор относительных оценок c при помощи правила скалярного произведения

c j = cj - c b× S j,

где

с b - вектор оценок базисных переменных;

S j - j-тый столбец в канонической системе, соответствующей рассматриваемому базису.

Дополняем первоначальную таблицу c – строкой (табл. 9.4).

Таблица 9.4

cb xb c1 c2 ... cm cm+1 ... cn b i
  базис x1 x2 ... xm xm+1 ... xn  
с1 x1     ...   a 1,m+1 ... a1 n b1
с2 x2     ...   a 2,m+1 ... a2 n b2
... ... ... ... ... ... ... ... ... ...
cm xm     ...   a m,m+1 ... am n b m
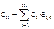
c – строка     ...   ... W

 

3. Если все оценки c j£0 (c j³0), i=1,...,n, то текущее допускаемое решение - максимальное (минимальное). Решение найдено.

4. В противном случае в базис необходимо ввести небазисную переменную xr с наибольшим значением c j вместо одной из базисных переменных (табл. 9.5).

Таблица 9.5

cb xb c1 c2 ... cm cm+1 ... cr ... cn b i
  базис x1 x2 ... xm xm+1 ... xr ... xn  
с1 x1     ...   a 1,m+1 ... a1 r ... A1 n b1
с2 x2     ...   a 2,m+1 ... a2 r ... A2 n b2
... ... ... ... ... ... ... ... ... ... ... ...
cm xm     ...   a m,m+1 ... am r ... am n b m
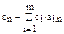
c - строка     ...   ... ... W
                max      

 

5. При помощи правила минимального отношения min(b i / a ir) определяем переменную xp, выводимую из базиса. Если коэффициент a ir отрицателен, то b i/ a ir = ¥. В результате пересечение столбца, где находится вводимая небазисная переменная xr, и строки, где находится выводимая базисная переменная xp, определит положение ведущего элемента таблицы (табл. 9.6).

Таблица 9.6

cb xb c1 c2 ... cm cm+1 ... cr ... cn b i b i/ a ir  
    x1 x2 ... xm xm+1 ... xr ... xn      
с1 x1     ...   a 1,m+1 ... a1 r ... a1 n b1 b1 / a 1r  
с2 x2     ...   a 2,m+1 ... a2 r ... a2 n b2 b2 / a 2r  
... ... ... ... ... ... ... ... ... ... ... ... ...  
сp xp     ...   a p,m+1 ... apr ... a pn bp bp / a pr m i n
... ... ... ... ... ... ... ... ... ... ... ... ...  
cm xm     ...   a m,m+1 ... am r ... am n b m b m/ a nr  
c -стро-ка     ...   ... ... W    
                max          

 

6. Применяем элементарные преобразования для получения нового допускаемого базового решения и новой таблицы. В результате ведущий элемент должен равняться 1, а остальные элементы столбца ведущего элемента примут нулевое значение.

7. Вычисляем новые относительные оценки с использованием правила скалярного произведения и переходим к шагу 4.

В качестве примера решим задачу ЛП примера 9.1 Оптимизация размещения побочного производства лесничества:

5000 x1 + 2500 x2 ® max,

4 x1 + 1,5 x2 £ 24;

1200 x1 + 150 x2 £ 6000;

20 x1 + 20 x2 £ 200;

x1 ³ 2;

x1 ³ 0; x2 ³ 0.

Приведем задачу к стандартной форме:

 

5000 x1 + 2500 x2 ® max,

4 x1 + 1,5 x2 + x3 = 24;

1200 x1 + 150 x2 +x4 = 6000;

20 x1 + 20 x2 + x5 = 200;

x1 - x6 = 2;

x1... x6 ³ 0.

Приведем систему равенств к каноническому виду. Первые три уравнения имеют соответственно по базисной переменной x3, x4, x5, однако в четвертом она отсутствует, ввиду того, что при переменной x6 стоит отрицательный единичный коэффициент. Для приведения системы к каноническому виду используем метод искусственных переменных. Идея метода заключается в следующем. Введем искусственную переменную x7 в последнее уравнение

 

5000 x1 + 2500 x2 ® max,

4 x1 + 1,5 x2 + x3 = 24;

1200 x1 + 150 x2 +x4 = 6000;

20 x1 + 20 x2 + x5 = 200;

x1 - x6 + x7 = 2;

x1... x7 ³ 0.

Вспомогательная система имеет следующее допустимое базовое решение:

x1 = x2 = 0, x3 =24, x4= 6000, x5 = 200, x7 = 2.

Полученное решение недопустимо для первоначальной задачи, поскольку x7 положительно. С другой стороны, любое базисное решение вспомогательной системы, в котором x7 обращается в ноль, допустимо для исходной задачи. Этого можно добиться при помощи двухэтапного симплекс - метода:

1. Вводится искусственная целевая функция, равная сумме искусственных переменных (в нашем случае она одна), которая минимизируется при помощи симплекс - метода. Если минимальное значение вспомогательной задачи равно 0, то все искусственные переменные (x7 в частности) обращаются в нуль и получается допустимое базисное решение начальной задачи.

2. На втором этапе допустимое базовое решение, полученное на первом этапе, улучшается в соответствии с целевой функцией исходной задачи.

В соответствии с рассмотренным алгоритмом на первом этапе решаем симплекс - методом следующую задачу ЛП:

x7 ® min,

4 x1 + 1,5 x2 + x3 = 24;

1200 x1 + 150 x2 +x4 = 6000;

20 x1 + 20 x2 + x5 = 200;

x1 - x6 + x7 = 2;

x1... x7 ³ 0.

Строим первоначальную таблицу (табл. 9.7).

Таблица 9.7

cb xb               b i b i/ a ir  
  базис X1 x2 x3 x4 x5 x6 x7      
  x3   1.5             24/4  
  x4                 60/12  
  x5                 20/2  
  x7           -1     2/1 min
c строка -1             W=2    
    min                  

 

Очевидно, что первоначальную таблицу необходимо модифицировать путем введения в базис переменной x1 вместо x7. Строим смежную симплекс-таблицу (табл.9.8).

 

Таблица 9.8

cb xb               b i
  базис x1 x2 x3 x4 x5 x6 x7  
  x3   1,5         -4  
  x4             -1200  
  x5             -20  
  x1           -1    
c строка               W=0

 

В табл. 9.8 все коэффициенты в строке c положительны или равны нулю, поэтому текущее базисное решение оптимальное (минимальное), которое используем на втором этапе двухэтапного симплекс - алгоритма. С этой целью возвращаемся к первоначальной целевой функции W = 5000x1 + 2,5x2 и продолжаем вычисления в симплекс – таблицах (табл. 9.9 – табл. 9.11). В табл. 9.9 как переменная x2, так и x6 могут быть введены в базис, т.к. их коэффициенты в строке c положительны (решается задача минимизации). Вводим x2 исходя из того факта, что данная переменная отражает искомое количество партий деревьев и в результате расчетов должна находиться в базисе. В принципе, искусственная переменная x6 также может быть введена в базис на этом этапе, однако процедура расчетов при этом значительно удлинится.

Таблица 9.9

cb xb               b i b i/ a ir  
  базис x1 X2 x3 x4 X5 x6 x7      
  x3   1,5         -4   16/1,5  
  x4             -1200   360/15  
  x5             -20   16/2 m i n
  x1           -1     ¥  
c - строка             -5000 W=    
                       

 

Таблица 9.10

cb xb               b i b i/ a ir  
  ба-зис X1 x2 x3 x4 x5 x6 x7      
  x3         -0,075 2,5 -2,5   4/ 2,5 m i n
  x4         -7,5   -1050   240/105  
  x2         0,05   -1   8/2  
  x1           -1     ¥  
c - строка         -125   -5000 W=    
              max        

 

Таблица 9.11

cb xb               b i
  базис x1 x2 x3 x4 x5 x6 x7  
  x6     0,4   -0,03   -1 1,6
  x4     -420          
  x2     -0,4   0,08     6,4
  x1     0,4   -0,03     3,6
c -строка     -1000   -50     W=34000

 

Полученные в табл. 9.11 окончательные результаты полностью соответствуют оптимальному решению в графическом методе (см. рис. 9.1). Остается открытым вопрос о целочисленности получаемых результатов. Если в графической интерпретации задачи ЛП мы можем визуально оценить ситуацию и принять окончательное решение путем субъективного округления, то в табличном методе, а тем более при решении задачи на ЭВМ, требуется применение специальной процедуры, которая получила название целочисленное программирование.

9.5. Метод искусственных переменных

 

Для получения системы в каноническом виде, обладающей допустимым базисным решением, существует специальный метод. Сначала задача ЛП приводится к стандартной форме, в которой все переменные неотрицательные. Затем для каждого ограничения проверяется существование соответствующей базисной переменной. Если ее нет, то вводится новая искусственная переменная, играющая роль базисной для данного ограничения. После проверки всех ограничений получается система в каноническом виде и появляется возможность заполнить начальную симплексную таблицу. Так как введенные переменные не имеют отношения к существу задачи ЛП в исходной постановке, то необходимо добиться обращения в нуль искусственных переменных. Этого можно сделать с помощью двухэтапного симплекс-метода.

· Этап 1. Рассматривается искусственная целевая функция, равная сумме искусственных переменных, которая минимизируется при помощи симплекс-метода. Другими словами, производится исключение искусственных переменных. Если минимальное значение вспомогательной задачи равно нулю, то все искусственные переменные обращаются в нуль и получается допустимое базисное решение начальной задачи. Далее реализуется этап 2. Если минимальное значение вспомогательной задачи положительное, то по крайней мере одна из искусственных переменных также положительная, что свидетельствует о противоречивости начальной задачи, и вычисления прекращаются.

· Этап 2. Допустимое базисное решение, найденное на первом этапе, улучшается в соответствии с целевой функцией исходной задачи ЛП на основе симплекс-метода, т.е. оптимальная таблица этапа 1 превращается в начальную таблицу этапа 2, и изменяется целевая функция.

9.6. Анализ чувствительности в линейном программировании

 

Решение практической задачи нельзя считать законченным, если найдено оптимальное решение. Дело в том, что некоторые параметры задачи ЛП (финансы, запасы сырья, производственные мощности) можно регулировать, что, в свою очередь, может изменить найденное оптимальное решение. Эта информация получается в результате выполнения анализа чувствительности. Анализ чувствительности позволяет оценить влияние этих параметров на оптимальное решение. Если обнаруживается, что оптимальное решение можно значительно улучшить за счет небольших изменений заданных параметров, то целесообразно реализовать эти изменения. Кроме того, во многих случаях оценки параметров получаются путем статистической обработки ретроспективных данных (например, ожидаемый сбыт, прогнозы цен и затрат). Оценки, как правило, не могут быть точными. Если удается определить, какие параметры в наибольшей степени влияют на значение целевой функции, то целесообразно увеличить точность оценок именно этих параметров, что позволяет повысить надежность рассматриваемой модели и получаемого решения.

 
⇐ Предыдущая34353637383940414243Следующая ⇒

Date: 2016-07-25; view: 500; Нарушение авторских прав; Помощь в написании работы --> СЮДА...


mydocx.ru - 2015-2024 year. (0.006 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию