Графическое решение задачи линейного программирования

Задачи ЛП с двумя переменными поддаются решению графическим способом. Продемонстрируем данный способ на примере 9.1 “Оптимизация размещения побочного производства лесничества”:

5000 x₁ + 2500 x₂ ® max,

4 x₁ + 1,5 x₂ £ 24;

1200 x₁ + 150 x₂ £ 6000;

20 x₁ + 20 x₂ £ 200;

x₁ ³ 2;

x₁ ³ 0; x₂ ³ 0.

На первом шаге следует определить все возможные неотрицательные значения переменных x₁ и x₂, которые удовлетворяют ограничениям. С этой целью в декартовой системе координат (рис. 9.1) наносим линии, соответствующие уравнениям прямых

4 x₁ + 1,5 x₂ = 24;

1200 x₁ + 150 x₂ = 6000;

20 x₁ + 20 x₂ = 200;

x₁ = 2; x₁ = 0; x₂ = 0,

и заштриховываем область, в точках которой выполняются все ограничения. Каждая такая точка называется допустимым решением, а множество всех допустимых решений называется допустимой областью. Очевидно, что решение задачи ЛП состоит в отыскании наилучшего решения в допустимой области, которое, в свою очередь, называется оптимальным. В рассматриваемом примере оптимальное решение представляет собой допустимое решение, максимизирующее функцию 5000x₁ + 2500x₂. Значение целевой функции, соответствующее оптимальному решению, называется оптимальным значением задачи ЛП. В нашем случае для нахождения оптимального решения достаточно через любую из вершин допустимой области провести прямую целевой функции и вслед за этим путем параллельного переноса полученной прямой найти такие вершины, в которых происходит только касание с допустимой областью.

Максимальный доход в размере 34 тыс. руб. лесничество может извлечь, придерживаясь следующей стратегии - выращивая 3,6 бычка и 6,4 партии растениеводческой продукции. Однако окончательное решение должно быть представлено в целочисленной форме. Как правило, на практике полученные результаты округляют до ближайших целых, что может привести к достаточно грубым ошибкам. В разбираемом примере округление даст x₁=3 и x₂=6, что приводит к доходу в 30 тыс. руб. Однако достаточно удаленная от оптимального решения стратегия x₁=4 и x₂=5 приводит к более оптимистичному результату - к 32,5 тыс. руб. Более того, как будет показано далее, еще более далекая точка x₁=3 и x₂=7 приводит к аналогичному результату. Поэтому расчеты необходимо продолжить с использованием методов целочисленного программирования, которые будут изложены ниже.

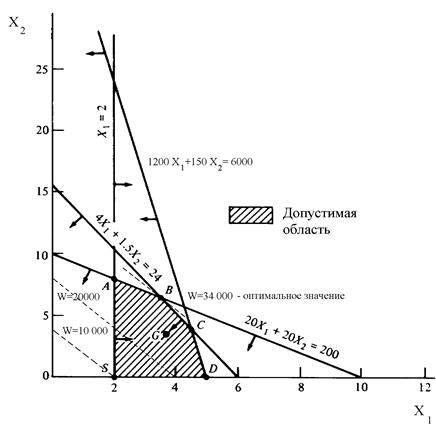
Рис. 9.1. Решение задачи ЛП графическим способом

Графический метод, ввиду большой размерности реальных практических задач ЛП, достаточно редко применяется, однако он позволяет ясно представить одно из основных свойств ЛП: если в задаче ЛП существует оптимальное решение, то по крайней мере одна из вершин допустимой области представляет собой оптимальное решение. Несмотря на то, что допустимая область задачи ЛП состоит из бесконечного числа точек, оптимальное решение всегда можно найти путем целенаправленного перебора конечного числа ее вершин. Рассматриваемый далее симплекс-метод решения задачи ЛП основывается на этом фундаментальном свойстве. Прежде чем перейдем к непосредственному применению симплекс-метода, всякая практическая задача должна быть сведена к стандартной форме.

9.3. Задача линейного программирования в стандартной форме