Основные правила дифференцирования

Ю. В. МИНЧЕНКОВ

ВЫСШАЯ МАТЕМАТИКА

Производная функции.

Дифференциал функции

Учебно-методическое пособие

Минск 2007

УДК 51

ББК 22.11я73

М 62

Рекомендовано к изданию редакционно-издательским советом
Частного института управления и предпринимательства

А в т о р

заведующий кафедрой высшей математики и статистики
Частного института управления и предпринимательства,
кандидат физико-математических наук, доцент Ю. В. Минченков

Минченков, Ю. В.

М 62 Высшая математика. Производная функции. Дифференциал функции: учеб.-метод. пособие / Ю. В. Минченков.– Минск: Частн. ин-т упр. и предпр., 2007.– 20 с.

Пособие подготовлено в соответствии с рабочей программой ЧИУиП по дисциплине «Высшая математика». Лекции охватывают основное содержание тем «Производная функции», «Правило Лопиталя. Дифференциал функции», примеры, задачи для самостоятельного решения.

Предназначено для студентов Частного института управления и предпринимательства.

УДК 51

ББК 22.11я73

© Минченков Ю. В., 2007

© Частный институт управления и предпринимательства, 2007

Лекция 1. ПРОИЗВОДНАЯ ФУНКЦИИ

План

1. Производная функции, ее геометрический и экономический смысл. Основные правила дифференцирования. Производные основных элементарных функций.

2. Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков.

Ключевые понятия

Правила дифференцирования. Производная функции. Уравнение касательной. Уравнение нормали. Производные суммы, произведения, частного двух функций. Производная сложной функции. Производные высших порядков.

1. Производная функции, ее геометрический
и экономический смысл.
Основные правила дифференцирования.
Производные основных элементарных функций

Пусть функция f (х) определена в некоторой окрестности точки х ₀.

Производной функцииf (х) в точке х ₀ называется число, обозначаемое f ¢ (х ₀) и равное

, (1)

если этот предел существует.

Так как х = х ₀ + ∆ х, х – х ₀ = ∆ х, то предел (1) может быть записан в виде

, (2)

то есть производная функции f (x) в точке х ₀ есть предел отношения ее приращения ∆ f (х ₀) в этой точке к соответствующему приращению аргумента ∆ х, когда ∆ х стремится к нулю.

Для обозначения производной функции f (x) в точке х ₀ используют следующие выражения:

.

Правой производной называется число

. (3)

Аналогично определяется левая производная .

Заметим, что существование производной функции в точке равносильно равенству ее односторонних производных в этой точке.

ПРИМЕР 1

Используя определение производной, найти для функции
f (x) = 4 x ² – 1.

Решение

Ответ: = 24.

ПРИМЕР 2

Найти односторонние производные функции f (x) = | x | в точке х ₀ = 0.

Решение

Таким образом, функция f (x) = | x | в точке х ₀ = 0 не имеет производной, так как односторонние производные не совпадают.

Ответ: = 1, .

Выясним геометрический смысл производной.

Пусть f (х) – непрерывная функция, определенная в некоторой окрестности точки х ₀. Рассмотрим две точки А (х ₀, f (х ₀)) и В (х ₁, f (х ₁)), лежащие на графике функции f (х) (см. рисунок).

Прямая l = АВ называется секущей. Запишем ее уравнение, используя уравнение прямой, заданной двумя точками:

l: .

Выразим из этого уравнения у:

, (4)

где

Пусть точка В стремится к точке А по графику функции f (x). Тогда секущая АВ будет стремиться к некоторому предельному положению. Это предельное положение секущей называется касательной к графику функции f (x) в точке х ₀. При этом касательная существует, если существует конечный предел

,

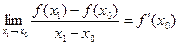который называется угловым коэффициентом касательной к графику функции f (x) в точке х ₀. Из (4) следует, что

(5)

– уравнение касательной к графику f (x) в точке х ₀. Таким образом,

,

где α – угол наклона касательной к положительному направлению оси О х.

Следовательно, с геометрической точки зрения, производная функции f (x) в точке х ₀ численно равна тангенсу угла, образованного касательной к графику функции f (x) в точке х ₀ и положительным направлением оси О х.

Прямая, перпендикулярная к касательной графика функции f (x) в точке , называется нормалью к кривой, определяемой функцией f (x), в точке х ₀. Учитывая, что для перпендикулярных прямых k ₁ k ₂ = –1, из (5) получаем уравнение нормали к графику функции f (x) в точке х ₀:

. (6)

Углом φ между двумя кривыми у = f ₁(х) и у = f ₂(х) в точке их пересечения с абсциссой х ₀ назовем угол между касательными к этим кривым, проведенными к ним в этой точке.

. (7)

Выясним теперь экономический смысл производной.

Пусть функция у = f (х) устанавливает зависимость выпуска продукции от затрат ресурса х. Пусть ресурс х получает прирост Δ х. Тогда будет приращением выпуска продукции, а отношение – средним приращением выпуска продукции на единицу затрат. Следовательно, производная выражает предельный продукт при затратах х и характеризует собой приближенно дополнительный выпуск продукции на единицу дополнительных затрат.

Если функция у = f (t) выражает количество произведенной продукции за время t, то f '(t) есть предельная производительность в момент времени t. Аналогичным образом могут быть определены предельные издержки, предельный доход, предельная выручка и т. д.

Отметим, что если функция f (х) имеет производную в точке х ₀, то она непрерывна в этой точке. Действительно, так как , то , где = 0 (теорема о связи предела функции и бесконечно малой функции). Следовательно

то есть по необходимому и достаточному условию непрерывности функции в точке х ₀ функция f (х) непрерывна в точке х ₀.

Операция вычисления производной функции называется дифференцированием. Функция, имеющая производную в точке, называется дифференцируемой в этой точке.

Основные правила дифференцирования

ТЕОРЕМА 1. Если функции u = u (x) и v = v (x) дифференцируемы в точке х, то функции u + v, uv, дифференцируемы в этой точке, причем:

1) ú;

2)

3) ;

4)

ТЕОРЕМА 2 (производная сложной функции). Если функция g (x) дифференцируема в точке х ₀, а функция f (у) дифференцируема в точке у ₀ = g (x ₀), то сложная функция f (g (x)) дифференцируема в точке х ₀ и

или .

Таблица основных производных

1) с' = 0, с ú;

2) х ' =1;

3) (хⁿ)' = nx^n-1, n ú;

4) (а^х)' = а^х ln а, 0 < a ¹ 1;

5) (e^x)' = e^x;

6) 0 < a ¹ 1, х > 0;

7) х > 0;

8) (sin x)' = cos x;

9) (cos x)' = – sin x;

10) ù;

11) ù;

12) ;

13) ;

14) ;

15) .

ПРИМЕР 3

Найти уравнения касательной и нормали к графику функции f (x)=
= 3 х ² + 4 в точке х ₀ = 2.

Решение

Найдем производную функции f (x): f' (x) = 6 х.

Для того чтобы составить уравнения касательной и нормали (5) и (6), необходимо найти значения функции и ее производной в точке х ₀ = 2:

f (2) = 3 × 2² + 4 = 16,

f ' (2) = 6 × 2 = 12.

Следовательно, уравнение касательной имеет вид:

у = 12 (х – 2) + 16,

уравнение нормали:

Ответ: у = 12 (х – 2) + 16,

ПРИМЕР 4

Найти производные функций.

а) ;

б) ;

в) ;

г) .

Решение

а) ;

б)

;

в) ;

г)

В примере г) мы вначале взяли производную степенной функции, затем производную sin 8 x, а в конце производную 8 х.

2. Логарифмическое дифференцирование.
Производная неявной функции.
Производные высших порядков

Логарифмическое дифференцирование применяют тогда, когда нужно найти производную выражения, содержащего произведения, корни, степени, то есть выражение, которое легко логарифмируется, а также для нахождения производной степенно-показательной функции u (x) ^{v ( x )}.

ПРИМЕР 5

Найти производную функции.

а) ;

б) .

Решение

а) прологарифмируем функцию у

Находим производную левой и правой частей данного выражения, учитывая, что :

Þ

б) прологарифмируем степенно-показательную функцию . (Степенно-показательная функция – это функция, у которой функциями являются и основание и показатель степени).

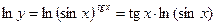
Находим производную левой и правой частей данного выражения:

.

Функция называется заданной неявно, если она представлена в виде

F (x, y) = 0,

то есть «у» не выражен явно, или его, в принципе, нельзя выразить явно через х. В этом случае производная находится, учитывая, что «у» – функция. Например, .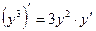

ПРИМЕР 6

Найти производную.

Решение

Продифференцируем данное выражение

Þ

Второй производной от функции у = f (x) называется производная от ее первой производной у '= f '(x). Обозначается вторая производная следующим образом: у '', f '', 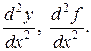Аналогично определяются производные третьего и более высоких порядков. Например, производная сотого порядка обозначается как у ⁽¹⁰⁰⁾ или .

ПРИМЕР 7

Найти производные функции

Решение

у ' = 20 х ⁴ + 4 х,

у '' = 80 х ³ + 4,

у ''' = 240 х ²,

у ⁽⁴⁾ =

у ⁽⁵⁾ = 480,

у ⁽⁶⁾ = 0.

Заметим, что для степенной функции количество производных, отличных от нуля, равно наивысшей степени функции. В данном примере пять производных не равны нулю.

Лекция 2. ПРАВИЛО ЛОПИТАЛЯ.
ДИФФЕРЕНЦИАЛ ФУНКЦИИ

План

1. Раскрытие неопределенностей при помощи правила Лопиталя.

2. Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях.

Ключевые понятия

Правило Лопиталя. Дифференциал функции. Раскрытие неопределенностей.

1. Раскрытие неопределенностей при помощи
правила Лопиталя

При вычислении пределов функции часто возникают неопределенности видов:

Раскрыть эти неопределенности помогает правило Лопиталя:

ПРИМЕР 1

а) ;

б) ;

в)
т. к. (первый замечательный предел).

Рассмотрим остальные неопределенности:

1) . Пусть , тогда , т. е. мы свели данную неопределенность к или , после чего можно применять правило Лопиталя;

2) , тогда ;

3) . Данные неопределенности также сводятся к неопределенностям или . Для этого можно воспользоваться формулой

Так, если то получаем неопределенность (т. к. , после чего можно получить или (смотри выше).

ПРИМЕР 2

а)

;

б)

.