Скалярное произведение векторов

Вектором называется направленный отрезок где точка А – начало вектора, точка В – конец вектора. Если начало и конец вектора в явном виде не указаны, то вектор будем обозначать и т. д.

Вектор, у которого начало и конец совпадают, называется нулевым вектором и обозначается .

Длиной (модулем) вектора называется длина его направленного отрезка и обозначается , .

Вектор, длина которого равна единице, называется единичным или ортом.

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Два вектора и называются равными , если они коллинеарны, имеют одинаковую длину и одинаковое направление.

Свободный вектор – это вектор, который можно переносить параллельно самому себе в любую точку пространства (плоскости).

Произведением вектора на число называется вектор , длина которого ; направление совпадает с направлением вектора , если 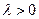, и противоположно ему, если .

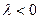Суммой двух векторов и называется вектор (рис. 1) и обозначается .

Разностью двух векторов и называется вектор и обозначается (рис. 2).

Векторы, лежащие в одной плоскости или на параллельных плоскостях, называются компланарными.

Декартовой прямоугольной системой координат в пространстве (прямо-угольной) называется совокупность трех упорядоченных взаимно перпендикулярных осей координат ОХ, ОY, OZ с общим началом в точке О. Орты координатных осей ОХ, ОY, ОZ обозначают соответственно. Векторы образуют декартовый прямоугольный базис в пространстве.

Базисом на плоскости 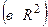называется упорядоченная пара любых некомпланарных векторов этой плоскости.

Базисом в пространстве называется упорядоченная тройка любых некомпланарных векторов.

Векторы , в пространстве образуют базис тогда и только тогда, когда определитель матрицы, составленной из их координат,

не равен нулю: .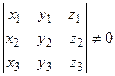

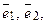Если – базис на плоскости, то любой вектор этой плоскости единственным образом представляется в виде линейной комбинации векторов т. е. .

Числа называют координатами векто ра в базисе и записывают .

Если 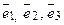– базис в пространстве, то любой вектор единственным обра-зом представляется в виде линейной комбинации векторов , т. е. . Числа называют координатами вектора в базисе и записывают .

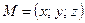Координатами точки М в заданной системе координат называют координаты ее радиус-вектора . В этом случае пишут или

Любой вектор в пространстве единственным образом представляется в виде линейной комбинации векторов т. е. . Числа называют декартовыми прямоугольными координатами вектора и записывают .

Линейные операции над векторами в координатной форме: пусть , , тогда , .

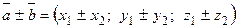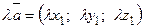Длина вектора вычисляется по формуле

. (2.1)

Если вектор задан координатами точек и , то

. (2.2)

Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

. (2.3)

Скалярное произведение в координатной форме:

. (2.4)

Из определения скалярного произведения следует, что

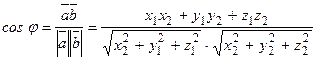. (2.5)

По значению косинуса находится угол между ненулевыми векторам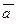и и .

Ненулевые векторы и перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю:

. (2.6)

Ненулевые векторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:

. (2.7)

Проекция вектора на вектор вычисляется по формуле 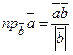. (2.8)

Примеры

1. Даны координаты точек , .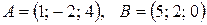

Вычислить длину вектора

.

Р е ш е н и е. Найдем координаты векторов по формуле (2.2):

.

Найдем координаты вектора

= .

Тогда длина вектора находится по формуле (2.1):

31,6.

2. Упростить выражение .

Р е ш е н и е. Воспользуемся свойствами скалярного произведения:

.

3. Определить, перпендикулярны ли векторы и , если , .

Р е ш е н и е. Векторы и имеют координаты:

Вычислим по формуле (2.4) скалярное произведение

.

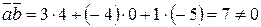Следовательно, векторы и не перпендикулярны, так как не выполняется условие перпендикулярности (2.6).

4. Найти координаты вектора , коллинеарного вектору 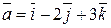при условии .

Р е ш е н и е. Из условия коллинеарности векторов (2.7) следует, что существует число , такое что 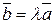. Тогда .

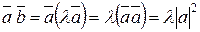Из условия задачи следует .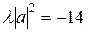

Тогда .

Следовательно, или

.

5. При каком значении параметра векторы и :

1) коллинеарны;

2) перпендикулярны?

Р е ш е н и е. 1) Из условия коллинеарности векторов (2.7) следует

.

Из пропорции 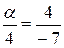найдем значение .

Date: 2016-07-25; view: 346; Нарушение авторских прав