
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Рассмотрим практические упражнения.
1. Дискретная случайная величина Х дана таблицей распределения вероятностей
| Х | |||
| P | 0,3 | 0,6 | 0,1 |
Вычислить числовые характеристики М (Х), D (X),  , V(X).
, V(X).
Находим математическое ожидание
 .
.
Дисперсию вычислим по формуле
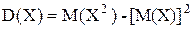 .
.
Составим закон распределения для случайной величины 

| |||
| P | 0,3 | 0,6 | 0,1 |
Вычислим  .
.
Итак,
D(X) = 10,2 -  .
.
Находим среднее квадратическое отклонение
 .
.
Определим коэффициент вариации
 %.
%.
2. Две независимые дискретные случайные величины даны таблицами распределения вероятностей
| X |  2 2
| 
|
| P | 0,6 | 0,4 |
| Y | 
| 
| 
|
| P | 0,6 | 0,3 | 0,1 |
Определить: М (2X + 3Y), D (X + 2), D (3X + 2Y), M (2XY).
Составить таблицу распределения вероятностей для случайной величины X + Y.
При вычислении числовых характеристик воспользуемся их свойствами. Для этого предварительно вычислим M(X), D(X), M(Y), D(Y).
Имеем
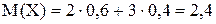 ;
;  ;
;

На основании свойств линейности математического ожидания имеем
М (2X + 3Y) = 2M (X) +3M(Y) = 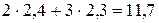 ; Далее на основании свойства 4 дисперсии имеем D (X + 2) = D(X) = 0,24;
; Далее на основании свойства 4 дисперсии имеем D (X + 2) = D(X) = 0,24;
C учетом свойств дисперсии 4 и 5 получим
D (3X + 2Y) = 9D(X) + 4D(Y) =  12,6.
12,6.
На основании свойства 4 математического ожидания имеем

Теперь составим закон распределения случайной величины X+Y.
Возможные значения случайной величины X+Y равны всевозможным суммам случайной величины Х со случайной величиной Y, то есть:
 ,
,
 .
.
Находим вероятности возможных значений. В частности,  . Так как случайные величины X, Y независимые, поэтому события
. Так как случайные величины X, Y независимые, поэтому события  в свою очередь являются независимыми. По теореме умножения вероятностей независимых событий имеем
в свою очередь являются независимыми. По теореме умножения вероятностей независимых событий имеем
 .
.
Итак,

Аналогично,
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Теперь составим таблицу распределения вероятностей для случайной величины X+Y
| X+Y | ||||||
| P | 0,36 | 0,24 | 0,18 | 0,12 | 0,06 | 0,04 |
Замечание. В качестве самоконтроля следует проверить сумму элементов второй строки, то есть, равна ли единице. В самом деле, имеем
0,36 + 0,24 + 0,18 + 0,12 + 0,06 + 0,04 = 1.
3. Дана плотность распределения непрерывной случайной величины X
 .
.
Найти: Функцию распределения F(x); математическое ожидание; дисперсию; среднее квадратическое отклонение; коэффициент вариации; P(1 < X < 6); Построить графики функций f (x), F (x).
Пользуясь формулой  , найдем интегральную функцию распределения F(x). Будем искать по промежуткам для любого
, найдем интегральную функцию распределения F(x). Будем искать по промежуткам для любого  имеем
имеем

Если  , то
, то

При  >2, имеем
>2, имеем

Итак, функция распределения
 .
.
Находим математическое ожидание
 .
.
Определим дисперсию по формуле
 . Итак,
. Итак, 
Находим  .
.
Определим коэффициент вариации
 %.
%.
Вычислим P (1 < X < 6) при помощи интегральной функции
 .
.
Если же дана плотность распределения, то можно найти следующим образом
 .
.
Формула Лапласа
Вернемся к нормальному распределению. Пусть случайная величина Х распределена по нормальному закону. Плотность распределения имеет вид
 . При этом М(Х) = а,
. При этом М(Х) = а,  ,
,  .
.
Итак, второй параметр  выражает среднеквадратическое отклонение нормального распределения. Определим вероятность попадания нормальной случайной величины в интервал
выражает среднеквадратическое отклонение нормального распределения. Определим вероятность попадания нормальной случайной величины в интервал  по формуле Лапласа
по формуле Лапласа
 ,
,
где  , где Ф (t) – функция Лапласа.
, где Ф (t) – функция Лапласа.
Пример 1. На прядильной фабрике вырабатывается пряжа, средняя прочность образцов которой равна 260 сн;  . Прочность как случайная величина приближенно следует нормальному закону распределения. Определить долю образцов пряжи с прочностью от 224 сн до 287 сн.
. Прочность как случайная величина приближенно следует нормальному закону распределения. Определить долю образцов пряжи с прочностью от 224 сн до 287 сн.
Поскольку прочность образцов пряжи Х согласно условию имеет приближенно нормальное распределение, поэтому можно использовать формулу Лапласа. В нашем случае параметры распределения такие: а=260 сн, и  .
.
Причем  . Находим сначала
. Находим сначала 
 .
.
Итак, по формуле Лапласа имеем

Значения функции Лапласа Ф (1,5) и Ф (2) нашли по таблице значений функции Лапласа.
Пример 2. Средняя прочность образцов пряжи равна 280 сн. 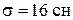 . Определить долю образцов всей пряжи, прочность которой отклоняется от средней на величину не больше 20 сн. Считается, что прочность приближенно изменяется по нормальному закону.
. Определить долю образцов всей пряжи, прочность которой отклоняется от средней на величину не больше 20 сн. Считается, что прочность приближенно изменяется по нормальному закону.
Здесь используем частный случай формулы Лапласа
 . В рассматриваемом примере а =280,
. В рассматриваемом примере а =280,  . Итак, имеем
. Итак, имеем
 .
.
Date: 2016-07-25; view: 310; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |