Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Линейные дифференциальные уравнения с постоянными
Коэффициентами
Линейное однородное уравнение n -го порядка с постоянными коэффициентами записывается в общем виде так
(21)
где 
- действительные постоянные.
Алгебраическое уравнение
(22)
полученное заменой производных искомой функции степенями, называется характеристическим уравнением для уравнения (21). При помощи корней характеристического уравнения можно записать так называемую фундаментальную систему частных решений, которая позволяет составить общее решение уравнения (21). Поскольку частные решения, составляющие фундаментальную систему решений, зависят от вида корней характеристического уравнения, поэтому уместно составить следующую таблицу
| Характер корня характеристического уравнения (22) | Частные решения уравнения (21) |
| 1. l - простой вещественный корень | 
|
| 2. l - вещественный корень кратности к | , x ,  ,..., 
|
| 3. a ± b i – простые комплексные сопряженные корни | 
|
| 4. a ± b i - комплексные сопряженные корни кратности к | 
|
Пусть 
фундаментальная система частных решений уравнения (21). Тогда 
общее решение этого уравнения.
З а д а ч а 6. Найти общее решение уравнения
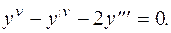
Запишем характеристическое уравнение
Корни 
простые, а 
корень кратности 3.
По найденным корням с учетом приведенной таблицы составим фундаментальную систему решений
Общее решение имеет вид
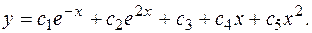
Задача 7. Найти общее решение уравнения
Методом подбора найдем один корень l 
=2 характеристического уравнения
l 
+ 4l 
+ l - 26 = 0.
Разделим
Итак,
Откуда
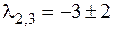i (
Составим по корням (см. таблицу) фундаментальную систему частных решений
Тем самым общее решение устанавливаем в виде
3. Линейное неоднородное уравнение n - го порядка с постоянными коэффициентами в общем виде имеет такой вид
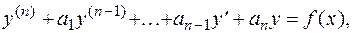(23)
где - действительные постоянные, а f (x) 
Общее решение уравнения (23) можно записать так: y = 
где 
- общее решение соответствующего однородного уравнения, а 
- любое частное решение уравнения (23).
Задача 8. Найти общее решение уравнения
Сначала найдем общее решение однородного уравнения 
Корни характеристического уравнения 
такие: 
i.
Составим фундаментальную систему частных решений
Общее решение однородного уравнения запишется
Частное решение неоднородного уравнения будем искать методом вариации произвольных постоянных
где функции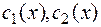 
подлежат определению. Составим систему
Отсюда находим
Интегрируем
Возьмем 
Следовательно, общим решением уравнения будет
Метод вариации произвольных постоянных является универсальным способом нахождения частных решений линейного неоднородного уравнения.
Если же правая часть f (x) уравнения (23) имеет вид
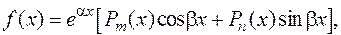
где 
многочлены соответственно степени m и n относительно переменной x, то частное решение можно искать методом неопределенных коэффициентов.
В частности, если 
i не является корнем характеристического уравнения, соответствующего однородного уравнения, то частное решение следует искать в виде
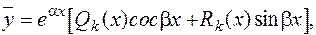
где 
многочлены степени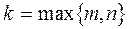 
с неопределенными коэффициентами.
Если i - корень характеристического уравнения кратности r, то
Задача 9. Найти общее решение уравнения
.
Корни характеристического уравнения 
такие:
Правая часть уравнения f (x) = 
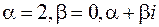- простой корень характеристического уравнения. С учетом вышеуказанных теоретических сведений частное решение будем искать в виде
Находим:
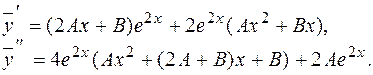
Подставив 
в данное уравнение и сократив обе части его на 
получим
10 Ax+ 2 A+ 5 B= x.
Приравнивая коэффициенты при одинаковых степенях, будем иметь систему
Отсюда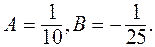 
Итак,
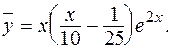
Общее решение исходного уравнения примет вид
+ 
Задача 10. Найти общее решение уравнения
Корни характеристического уравнения 
равны
не является корнем характеристического уравнения. Тем самым частное решение запишется в виде
Продифференцируем
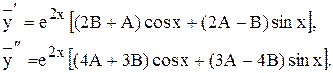
Подставляя 
в исходное уравнение, получаем
-2 A sin x - 2 B cos x = sin x.
Приравнивая коэффициенты при функциях sin x и cos x, будем иметь
Отсюда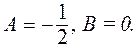 
Итак,
Общее решение уравнения
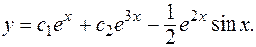
2.3 Системы дифференциальных уравнений
Система дифференциальных уравнений вида
,
где 
- неизвестные функции от независимой переменной 
, правые части представляют заранее заданные функции от переменных , , называется нормальной системой.
Напомним, что для нормальной системы смысл теоремы Коши (существования и единственности решения) состоит в следующем: если правые части системы непрерывны и имеют непрерывные частные производные по переменным в некоторой области D, то для любой точки 
существует единственное решение в некоторой окрестности точки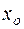 
,
удовлетворяющее начальным условиям
.
Общее решение нормальной системы представляет множество функций
,
зависящих от n параметров, которые при любых допустимых значениях параметров 
обращают каждое уравнение системы в тождество, в области, в которой выполнены условия теоремы Коши и кроме того, из этой совокупности функций можно выделить любое решение задачи Коши.
Уравнение
можно свести к нормальной системе. Действительно, введем новые переменные
, в результате получим эквивалентную нормальную систему уравнений
.
Таким образом, приведенный подход позволяет свести решение дифференциального уравнения n – го порядка к решению нормальной системы n уравнений первого порядка. Именно такой подход часто используется при численном интегрировании дифференциальных уравнений высших порядков.
Многие основные теоретические положения для нормальных систем аналогичны дифференциальным уравнениям высших порядков в силу их вышеуказанной взаимосвязи. Поэтому ограничимся весьма кратким рассмотрением вопросов, связанных системами дифференциальных уравнений.
При решении систем дифференциальных уравнений весьма часто используется метод исключения неизвестных.
Проиллюстрируем на примере решения линейной однородной системы с постоянными коэффициентами.
Задача 1. Найти общее решение системы. Выделить частное решение, удовлетворяющее начальным условиям:
Имеем линейную однородную систему с постоянными коэффициентами. Решим методом исключения неизвестных. Дифференцируем первое уравнение по t:
Подставляя вместо 
из 2-го уравнения, получим
Выразим y из 1-го уравнения и подставим в последнее уравнение, в итоге будем иметь линейное однородное уравнение с постоянными коэффициентами
Найдем его общее решение. Корни характеристического уравнения
равны 
Итак, 
(24)
Далее найдем вторую неизвестную функцию, используя (24)
Кроме того, с учетом начальных условий, получим: 
Ответ:
Замечание. Итак, линейные однородные системы с постоянными коэффициентами сводятся к решению линейных однородных уравнений высших порядков с постоянными коэффициентами. Аналогичное положение имеет место и для линейных неоднородных систем с постоянными коэффициентами. Можно найти общее решение линейной однородной системы с постоянными коэффициентами также через корни характеристического уравнения и т.д.
При помощи дифференциальных уравнений описываются многие физические и механические процессы, природные явления и т.д., то есть, научные достижения в этой области имеют весьма разнообразные и глубокие теоретические и прикладные приложения во многих областях знаний, а также широко используются при решении инженерных, экономических и прикладных задач практического характера. Одним словом, в современном мире диапазон приложений теории дифференциальных уравнений очень широкий.
2.4 Задачи на составление дифференциальных уравнений
В заключение рассмотрим некоторые простейшие задачи геометрического и физического характера, связанные с составлением дифференциальных уравнений и нахождением их решений с учетом начальных условий.
Задача 1. Найти уравнение кривой, проходящей через точку 
, если ее подкасательная вдвое больше абсциссы точки касания.
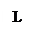
Построим схематический чертеж. Пусть y = y(x) описывает искомую кривую.
Прямые MN и ML означают соответственно касательную и нормаль к кривой y = y(x) в точке M. MQ 
OX. Длина отрезка 
называется подкасательной, а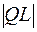 
- поднормалью.
При этом справедливы формулы: 
.
Date: 2016-07-25; view: 287; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |