Уравнения, не разрешенные относительно производной

Рассмотрим теперь случай уравнения первого порядка

F (x, y, 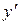) = 0, (18)

не разрешенного относительно производной .

Так же как и в случае уравнения, разрешенного относительно производной, кривые, подозрительные на особое решение уравнения (18), можно найти по семейству интегральных кривых Ф(x,y,C) = 0, как огибающую, исключая параметр С из системы уравнений

или по самому уравнению.

Поясним нахождение особого решения при помощи исходного уравнения (16). Предполагая, что существует , составляем систему уравнений

.

Кривая, получающаяся исключением из этой системы называется дискриминатной кривой уравнения (18). Она может быть особым решением уравнения, для этого, прежде всего, проверить является ли решением этого уравнения.

Таким образом, особым решением уравнения (18) может быть только дискриминатная кривая этого уравнения или семейства интегральных кривых. Дискриминатная кривая (или ее часть) будет особым решением в том случае, когда она (или ее часть) является огибающей семейства интегральных кривых (или части семейства). Не вникая в тонкости этого вопроса, отметим, что дискриминатная кривая может быть также геометрическим местом так называемых точек возврата интегральных кривых или точек прикосновения интегральных кривых различных ветвей решения уравнения (18).

Рассмотрим иллюстративные упражнения:

а) .

Общее решение этого уравнения имеет вид . При помощи исходного уравнения составим систему для определения дискриминатной кривой

.

Отсюда y = 0 - дискриминатная кривая. Она является особым решением, так как ось OX – огибающая семейства интегральных кривых.

б) . Это уравнение имеет два семейства интегральных кривых

. Или объединяя можно записать так

. Далее найдем дискриминатную кривую этого семейства интегральных кривых. Составляем систему ранее указанным образом

.

Отсюда исключая параметр С, находим дискриминатную кривую x = 0, то есть, ось OY. Заметим, что она не является огибающей данного семейства интегральных кривых. Следовательно, x = 0 не является особым решением, а является геометрическим местом точек прикосновения интегральных кривых уравнений

.

в) Уравнение 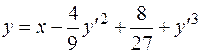имеет семейство интегральных кривых . Составим систему

.

Исключая С, находим дискриминатные кривые . Прямая y = x не является решением этого уравнения, можно убедиться непосредственной подстановкой. Она является геометрическим местом так называемых точек возврата. Вторая прямая является огибающей, следовательно, является особым решением.

Кроме того, особое решение может быть найдено следующим образом:

найти те решения уравнения, которые могли быть потеряны в процессе преобразований. Для этого надо проследить, не происходило ли в процессе преобразований нарушения равносильности уравнений, и если таковые были, то выявить те множители, которые могли давать решения исходного уравнения. Полученные таким путем функции следует подставить в исходное уравнение, чтобы проверить, действительно ли они являются решениями. После этого следует выяснить, не содержатся ли выявленные решения в записи общего решения. Если нет, то их надо дописать отдельно к общему решению уравнения.

Теперь, наконец, рассмотрим вопрос о нахождении общего решения уравнения (18), не разрешенного относительно производной.

1. Пусть уравнение F (x, y, 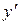) = 0 разрешимо относительно переменной y, то есть уравнение имеет вид

.

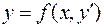Введем параметр р, полагая

.

Тогда получим

y = f (x, p).

Далее продифференцируя по переменной x, будем иметь

.

Получили уравнение, разрешенное относительно производной .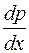

Из системы уравнений

определяют общее решение в явном или параметрической форме.

В частности, если уравнение имеет вид , то в этом случае переменная находится интегрированием

.

Решение в параметрической форме записывается в виде

.

1. Уравнение разрешимо относительно переменной x, то есть

Аналогично, положив , имеем x = f (y, p). Дифференцируя по переменной y, получим

.

Затем общее решение в рассматриваемом случае записывают в явном виде или параметрической форме.

Если же уравнение имеет вид ,

то в параметрической форме решение принимает вид

.

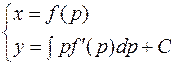Date: 2016-07-25; view: 419; Нарушение авторских прав