
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 2. Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Основные понятия и теоретические сведения
Рассмотрим необходимые теоретические сведения, а также параллельно изложим методы решения ряда типовых задач, разбор которых окажет студенту-заочнику существенную методическую помощь при выполнении контрольной работы.
Напомним, что уравнения вида
F (x, y, 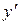 ) = 0 (1)
) = 0 (1)
где x - независимая переменная, y - искомая функция от x, 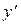 -
-  ее производная, называется дифференциальным уравнением первого порядка.
ее производная, называется дифференциальным уравнением первого порядка.
Если уравнение (1) можно разрешить относительно 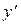 , то оно принимает вид
, то оно принимает вид
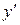 = f (x, y) (2)
= f (x, y) (2)
и называется уравнением первого порядка, разрешенным относительно производной. В некоторых случаях уравнение (2) удобно записать в виде
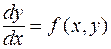
или в такой форме 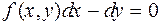 , являющимся частным случаем более общего уравнения
, являющимся частным случаем более общего уравнения
P (x, y) d x + G (x, y) d y = О, (3)
где P (x, y) и Q (x, y) - известные функции. Функция y = y (x), заданная на интервале (a, b), называется решением уравнения (1) или (2), если при подстановке в уравнение его обращает в тождество относительно x Î(a, b). График решения дифференциального уравнения называется интегральной кривой.
Ответ на вопрос о том, при каких условиях уравнение (2) имеет решение, дает теорема Коши.
Т е о р е м а Коши ( существования и единственности решения).
Пусть правая часть f (x, y) уравнения (2) определена в некоторой области D на плоскости OХY. Если существует такая окрестность 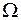 точки
точки 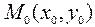 области D, в которой f (x, y) удовлетворяет условиям:
области D, в которой f (x, y) удовлетворяет условиям:
1. Непрерывна по совокупности аргументов;
2. Имеет ограниченную частную производную 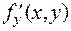 ,
,
то существует и причем единственное решение y = y (x) уравнения (2) в некоторой окрестности точки 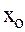 , удовлетворяющее условию y (x
, удовлетворяющее условию y (x 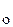 ) = y
) = y 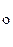 или пишут так:
или пишут так:

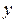
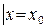
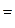
 .
. 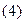
Замечание. Если в теореме требование ограниченности производной 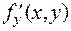 заменить выполнением условия Липшица:
заменить выполнением условия Липшица:
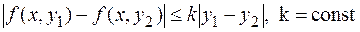 , то теорема Коши в такой формулировке остается в силе.
, то теорема Коши в такой формулировке остается в силе.
Геометрически теорема означает, что через точку M 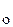 (x
(x 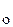 , y
, y 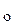 ) проходит единственная интегральная кривая уравнения (2). Эта теорема имеет локальный характер, она гарантирует существование единственности решения уравнения (2) лишь в достаточно малой окрестности точки
) проходит единственная интегральная кривая уравнения (2). Эта теорема имеет локальный характер, она гарантирует существование единственности решения уравнения (2) лишь в достаточно малой окрестности точки 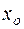 . Из этой теоремы следует, что уравнение (2) имеет бесконечное множество различных решений. Условие (4) называется начальным условием.
. Из этой теоремы следует, что уравнение (2) имеет бесконечное множество различных решений. Условие (4) называется начальным условием.
Отыскание решения уравнения (2), удовлетворяющего начальному условию (4), называется задачей Коши. С геометрической точки зрения решить задачу Коши означает: выделить из множества интегральных кривых ту, которая проходит через заданную точку M 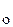 (x
(x 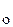 , y
, y 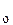 ).
).
Напомним понятие общего решения. Пусть D - некоторая область на плоскости охy, через каждую точку которой проходит единственная интегральная кривая уравнения (2). Однопараметрическое семейство функций y = j (x, C) параметра С называется общим решением уравнения (2), удовлетворяющего условиям теоремы Коши в области D, если при любом допустимом значении параметра C определяет решение этого уравнения и, кроме того, для любой внутренней точки M 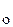 (x
(x 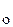 , y
, y 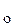 )
) 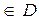 существует такое значение С= С
существует такое значение С= С 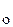 , что функция y = j (x, С
, что функция y = j (x, С 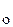 ) удовлетворяет начальному условию
) удовлетворяет начальному условию 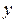
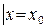
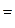
 .
.
Любая функция, выделенная из общего решения, называется частным решением.
Уравнение Ф (x, y, С) = О, определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Остановимся на следующих полезных упражнениях:
1. Рассмотрим уравнение 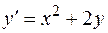 . В этом уравнении
. В этом уравнении
 определена и непрерывна во всех точках плоскости OХY и имеет
определена и непрерывна во всех точках плоскости OХY и имеет 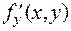 =2. В силу теоремы 1 через каждую точку M
=2. В силу теоремы 1 через каждую точку M 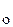 (x
(x 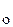 , y
, y 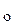 )
) 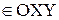 проходит единственная интегральная кривая этого уравнения.
проходит единственная интегральная кривая этого уравнения.
2. Дано уравнение 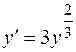 . Функция
. Функция 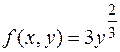 определена и непрерывна на всей плоскости OХY; однако,
определена и непрерывна на всей плоскости OХY; однако, 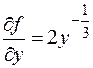 . Заметим, что во всех точках оси OX не выполняется второе условие теоремы Коши. Легко убедиться, что семейство функций
. Заметим, что во всех точках оси OX не выполняется второе условие теоремы Коши. Легко убедиться, что семейство функций 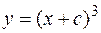 при любом С является решением данного уравнения. Кроме того, это уравнение имеет решение y = 0, т.е., ось OX. Если же искать решения этого уравнения, удовлетворяющие начальному условию y (0) = 0, то таких решений можно найти бесчисленное множество; в частности, такие
при любом С является решением данного уравнения. Кроме того, это уравнение имеет решение y = 0, т.е., ось OX. Если же искать решения этого уравнения, удовлетворяющие начальному условию y (0) = 0, то таких решений можно найти бесчисленное множество; в частности, такие
y = 0, 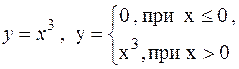 и т.д.
и т.д.
При этом через каждую точку 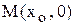 оси OX проходят по крайней мере две интегральные кривые y = 0 и
оси OX проходят по крайней мере две интегральные кривые y = 0 и 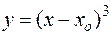 , то есть, в точках оси OX нарушается единственность решения.
, то есть, в точках оси OX нарушается единственность решения.
Если же взять точку 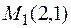 , то в достаточно малой ее окрестности выполнены все условия теоремы 1. Тем самым через данную точку в малом квадрате
, то в достаточно малой ее окрестности выполнены все условия теоремы 1. Тем самым через данную точку в малом квадрате 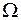 проходит единственная интегральная кривая
проходит единственная интегральная кривая 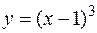 . Естественно, если же квадрат
. Естественно, если же квадрат 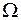 достаточно расширить, то в нем единственность решения не будет выполнена, что убеждает нас о локальном характере теоремы 1.
достаточно расширить, то в нем единственность решения не будет выполнена, что убеждает нас о локальном характере теоремы 1.
Теорема 1 дает лишь достаточные условия единственности решения уравнения (2). Однако, не исключается возможность существования единственного решения y = y (x), удовлетворяющего начальному условию  , хотя в точке M
, хотя в точке M 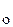 (x
(x 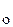 , y
, y 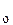 ) и не выполняются условия теоремы Коши. Можно было бы этот вариант тоже проиллюстрировать на примерах.
) и не выполняются условия теоремы Коши. Можно было бы этот вариант тоже проиллюстрировать на примерах.
Таким образом, мы вплотную подошли к необходимости рассмотрения так называемых особых решений дифференциальных уравнений (1) или (2).
2. Особые решения
Решение дифференциального уравнения первого порядка называется особым, если соответствующая интегральная кривая обладает тем свойством, что через каждую ее точку проходит, кроме нее, еще и другая касающаяся ее интегральная кривая данного уравнения.
Итак, особое решение уравнения (2) представляет такое решение, в каждой точке которого нарушается единственность решения задачи Коши.
Отсюда следует, что для существования особого решения уравнения (2) необходимо, чтобы не выполнялось хотя бы одно из условий теоремы 1.
В частности, для уравнения 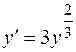 не выполняется второе условие, т.е., производная
не выполняется второе условие, т.е., производная 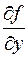 обращается в бесконечность на OX плоскости OХY. Для этого уравнения общее решение представляет семейство кубических парабол, причем решение y = 0 проходит через те точки, где производная
обращается в бесконечность на OX плоскости OХY. Для этого уравнения общее решение представляет семейство кубических парабол, причем решение y = 0 проходит через те точки, где производная 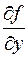 не ограничена. Итак, решение y = 0 – особое, так как через каждую его точку проходит другая интегральная кривая - кубическая парабола.
не ограничена. Итак, решение y = 0 – особое, так как через каждую его точку проходит другая интегральная кривая - кубическая парабола.
Замечание.Заметим, что особое решение не выделяется из общего решения (общего интеграла) при определенном значении параметра С.
Однако, не всякая кривая, в точках которой не выполнено условие ограниченности производной 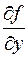 , может быть особой интегральной кривой.
, может быть особой интегральной кривой.
Например, для уравнения 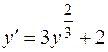 хотя в точках прямой y = 0 не выполняется условие ограниченности производной
хотя в точках прямой y = 0 не выполняется условие ограниченности производной 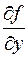 , но эта прямая не представляет особую интегральную кривую, поскольку не является даже решением этого уравнения.
, но эта прямая не представляет особую интегральную кривую, поскольку не является даже решением этого уравнения.
Таким образом, вышеприведенные рассуждения позволяют резюмировать для уравнения (2) при выполнении первого условия теоремы 1 следующее заключение; то есть, особые решения могут быть выявлены так:
1. Найти геометрическое место точек, в которых производная
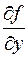 обращается в бесконечность.
обращается в бесконечность.
2. Если такие кривые окажутся, то проверить являются ли они интегральными кривыми уравнения (2).
3. Среди выявленных интегральных кривых проверить: нарушается ли в каждой из точек этих кривых свойство единственности.
При выполнении всех этих условий найденные кривые представляют особые решения уравнения (2).
Кроме того, следует подчеркнуть, что уравнение (2) может иметь решения, которые не являются ни частными, ни особыми. Таким примером является решение 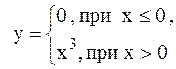 уравнения
уравнения 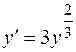 .
.
Если в любой окрестности точки M 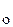 (x
(x 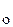 , y
, y 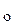 ) не выполняются условия теоремы Коши (1), то точка M
) не выполняются условия теоремы Коши (1), то точка M 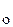 (x
(x 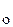 , y
, y 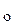 ) называется особой точкой уравнения (2). При этом особая точка M
) называется особой точкой уравнения (2). При этом особая точка M 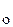 (x
(x 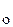 , y
, y 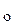 ) называется изолированной, если в некоторой достаточно малой ее окрестности нет других особых точек.
) называется изолированной, если в некоторой достаточно малой ее окрестности нет других особых точек.
Итак, прежде всего особое решение представляет интегральную кривую, состоящую из особых точек.
Пусть общее решение уравнения (2) допускает однопараметрическое семейство интегральных кривых Ф(x,y,C) = 0, где С – параметр. Допустим, что семейство кривых имеет огибающую, т.е., кривую, которая касается каждой кривой этого семейства и причем состоит полностью из этих точек касания. При этом заметим, что огибающая семейства интегральных кривых является особым решением уравнения (2).
Огибающая семейства интегральных кривых Ф(x,y,C) = 0 определяется из следующей системы уравнений
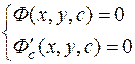 .
.
Второе уравнение системы составляется путем дифференцирования по параметру С первого уравнения. Находят кривую путем исключения параметра С из этой системы, если это возможно. Эта кривая называется дискриминантной. Затем найденную дискриминатную кривую проверяют, является ли она решением данного уравнения.
Таким образом, мы привели еще один весьма эффективный способ нахождения особых решений при помощи огибающих семейства интегральных кривых уравнения (2).
Date: 2016-07-25; view: 515; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |