
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические рекомендации по проведению элективного курса «Задачи с параметрами».
Занятие 1, 2 (параллельный перенос). Графические методы особенно эффективны при исследовании уравнений и неравенств, содержащих модули. Они позволяют сразу отобрать нужные для решения случаи, и не заниматься перебором всех случаев, которые имеют место при формальном раскрытии модулей. Поэтому на первом занятии мы вспомним, что такое модуль.
Модуль положительного числа а равен самому этому числу а. Модуль 0 равен 0. Модуль отрицательного числа а равен противоположному числу (- а).
 .
.
Так же напомним, что при каждом значении а график функции у=а представляет собой прямую, параллельную оси Ох. При разных а это разные прямые. Поэтому, когда а «пробегает» некоторое множество значений, уравнение у=а определяет на плоскости некоторое множество или семейство прямых, параллельных оси Ох.
Теперь перейдем к решению задач:
Задача 1. Сколько корней имеет уравнение  в зависимости от значений параметра а?
в зависимости от значений параметра а?
Решение. Построим графики функций  и
и  . Графиком функции
. Графиком функции  будет являться прямая параллельная оси Ох, при изменении значения параметра а прямая будет перемещаться выше, ниже по оси Оу. Другими словами, мы осуществляем параллельный перенос. Количество точек пересечения графиков функций
будет являться прямая параллельная оси Ох, при изменении значения параметра а прямая будет перемещаться выше, ниже по оси Оу. Другими словами, мы осуществляем параллельный перенос. Количество точек пересечения графиков функций  и
и  будет решением нашего уравнения.
будет решением нашего уравнения.

Рис.5.
Из рисунка 5 видно, что при а <0 точек пересечения нет, следовательно, нет решений уравнения. При а =0 или а >9 точек пересечения будет две, следовательно, уравнения имеет два решения. Если а =9, то уравнение имеет три решения, а при 0< а <9 уравнение имеет четыре решения.
Замечание: Ученики, которые знают приемы построения графиков с модулями, могли бы построить график  проще. Сначала построить график
проще. Сначала построить график  , а затем часть, которая находится под осью Ох, симметрично отобразить относительно оси Ох.
, а затем часть, которая находится под осью Ох, симметрично отобразить относительно оси Ох.
Задача 2. При всех а решить уравнение

Решение состоит из трех стандартных шагов. На первом шаге мы нарисуем графики функций  и
и  . На втором рассмотрим, в скольких точках пересекаются эти графики при различных значениях а. И на третьем найдем координаты точек пересечения этих графиков. Абсциссы этих точек и будут решениями.
. На втором рассмотрим, в скольких точках пересекаются эти графики при различных значениях а. И на третьем найдем координаты точек пересечения этих графиков. Абсциссы этих точек и будут решениями.
64. Графиком функции  будет уголок. Координаты вершины этого уголка х =1-4 а, у =0. Раскрыв знак модуля, получаем:
будет уголок. Координаты вершины этого уголка х =1-4 а, у =0. Раскрыв знак модуля, получаем:

Поскольку при разных значениях а это будут разные уголки с вершиной на оси Ох, то можно сказать, что изменением а уголки «движутся» вдоль оси Ох.
Графиком  является прямая с угловым коэффициентом k =
является прямая с угловым коэффициентом k = 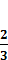 . При изменении а она буде перемещаться вверх или вниз вдоль оси Оу (рис.6).
. При изменении а она буде перемещаться вверх или вниз вдоль оси Оу (рис.6).
Таким образом, в данной задаче оба графика  и
и  зависят от параметра а и при изменении а будут сдвигаться: график
зависят от параметра а и при изменении а будут сдвигаться: график  вдоль оси Ох, а график
вдоль оси Ох, а график  - вдоль оси Оу. Однако на решение задачи это не влияет.
- вдоль оси Оу. Однако на решение задачи это не влияет.
1. Найдем в зависимости от а число пересечений этих графиков.
а) Если прямая  проходит ниже вершины уголка А (прямая
проходит ниже вершины уголка А (прямая  ), то графики не пересекаются. Это будет, если значение функции
), то графики не пересекаются. Это будет, если значение функции  в вершине х =1-4а меньше нуля. Имеем
в вершине х =1-4а меньше нуля. Имеем

b) Если прямая  проходит через вершину А, уравнение будет иметь одно решение (прямая
проходит через вершину А, уравнение будет иметь одно решение (прямая  ). Это имеет место, если
). Это имеет место, если 
Имеем

Решением в этом случае будет абсцисса вершины уголка. Подставляя а =4, находим х=1-4*4=-15.

Рис.6.
с) Если прямая  проходит выше вершины А то она будет пересекаться с двумя ветвями уголка (прямая
проходит выше вершины А то она будет пересекаться с двумя ветвями уголка (прямая  ) и уравнение будет иметь два решения. Последнее имеет место, если
) и уравнение будет иметь два решения. Последнее имеет место, если
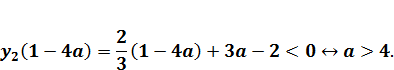
Найдем точки пересечения этой прямой с ветвями уголка. Пересечение прямой  и левой ветви
и левой ветви 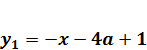 будет при
будет при  =
=  . Откуда находим
. Откуда находим  - первый корень уравнения. Пересечение с правой ветвью
- первый корень уравнения. Пересечение с правой ветвью  будет, когда
будет, когда 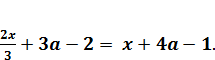 Из этого равенства находим второй корень исходного уравнения
Из этого равенства находим второй корень исходного уравнения  .
.
Ответ: при а <4 решений нет; при а =4 уравнение имеет одно решение х=-15; при а >4 два решения  и
и  .
.
Задача 3 (ЕГЭ 2011года). Найти все значения а, при каждом которых система 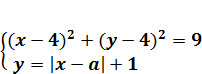 , имеет ровно три различных решения.
, имеет ровно три различных решения.
Решение. Первое уравнение системы задает окружность радиуса 3 с центром в точке О (4;4). Второе - прямой угол с вершиной в точке (а;1) и симметричный относительно прямой х=а. Прямая у =1 является касательной к окружности. Графики имеют ровно три точки в следующих случаях.
1. Вершина прямого угла лежит в точке касания окружности и прямой у =1 (точка М), а его стороны пересекают окружность в двух точках. Это условие выполняется при а =4.
2. Одна из сторон угла пересекает окружность в двух точках, а другая касается окружности. Таких случаев два.

Рис.7.
Ответ: а =4; а =7-3  и а =1+3
и а =1+3 
Замечание. В общем случае для определения абсциссы  точки касания графиков функций ʄ(x) и ƍ(х,а) и соответствующего значения параметра а используют то, что касающиеся графики в точке касания имеют общую касательную. Это означает в точке
точки касания графиков функций ʄ(x) и ƍ(х,а) и соответствующего значения параметра а используют то, что касающиеся графики в точке касания имеют общую касательную. Это означает в точке  равны значения функций ʄ(
равны значения функций ʄ( )= ƍ(
)= ƍ( ,а) и значения их производных ʄ’(
,а) и значения их производных ʄ’( )= ƍ’
)= ƍ’  ,а). В итоге получается система уравнений:
,а). В итоге получается система уравнений:
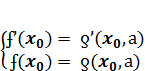
Занятие 3 (поворот). Прежде, чем переходить к решению следующих задач, рассмотрим условия, при которых прямая  касается параболы
касается параболы 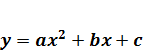 . Случай касания прямой и параболы означает, что они имеют только одну общую точку, это означает, что
. Случай касания прямой и параболы означает, что они имеют только одну общую точку, это означает, что  выполняется только при одном значении х. Или другими словами, что уравнение
выполняется только при одном значении х. Или другими словами, что уравнение 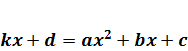 имеет ровно одно решение. Перенося все члены этого уравнения в одну сторону, приходим к квадратному уравнению. А квадратное уравнение имеет одно решение только в том случае, когда его дискриминант равен 0. Это и есть необходимое и достаточное условие касания прямой и параболы. Из сказанного сразу следует: если Д>0, то уравнение имеет два решения. А это означает, что прямая пересекает параболу в двух точках. И, наконец, если Д<0, то парабола и прямая не имеют общих точек.
имеет ровно одно решение. Перенося все члены этого уравнения в одну сторону, приходим к квадратному уравнению. А квадратное уравнение имеет одно решение только в том случае, когда его дискриминант равен 0. Это и есть необходимое и достаточное условие касания прямой и параболы. Из сказанного сразу следует: если Д>0, то уравнение имеет два решения. А это означает, что прямая пересекает параболу в двух точках. И, наконец, если Д<0, то парабола и прямая не имеют общих точек.
Задача 1. При всех а ≥0 определить число решений уравнения

Решение. Построим графики  и
и 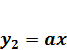 (рис.8). Построение графика
(рис.8). Построение графика  мы уже разбирали. График
мы уже разбирали. График 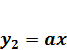 при всех а есть прямая, проходящая через начало координат.
при всех а есть прямая, проходящая через начало координат.
Рассмотрим два случая: а =0 и а >0.
Случай 1. а =0. Тогда  есть прямая, совпадающая с осью Ох. Она пересекает график
есть прямая, совпадающая с осью Ох. Она пересекает график  в двух точках
в двух точках  и
и  (рис.8). Следовательно, при а =0 уравнение имеет два решения.
(рис.8). Следовательно, при а =0 уравнение имеет два решения.
Случай 2. а >0. Тогда при «небольших» а, прямая 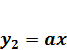 пересекает график
пересекает график  в четырех точках. Это будет до момента касания прямой
в четырех точках. Это будет до момента касания прямой 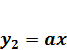 с параболой
с параболой 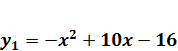 (прямая Ɩ2). Найдем, при каких а прямая
(прямая Ɩ2). Найдем, при каких а прямая 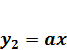 касается параболы.
касается параболы.
Как мы уже говорили, касание параболы и прямой равносильно тому, что уравнение

имеет одно решение. Это будет если D=0. Имеем
D= 
Итак, касание прямой 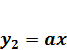 и параболы будет при двух значениях а. Но нам подходит только одно значение а =2. Потому что, мы рассматриваем не всю параболу, а только ее часть на промежутке [2;8] и при а =2, прямая будет касаться нашей параболы внутри рассматриваемого промежутка. При а =18 касание будет вне этого промежутка.
и параболы будет при двух значениях а. Но нам подходит только одно значение а =2. Потому что, мы рассматриваем не всю параболу, а только ее часть на промежутке [2;8] и при а =2, прямая будет касаться нашей параболы внутри рассматриваемого промежутка. При а =18 касание будет вне этого промежутка.

Рис.8.
Ответ: при а =0 и а >0 два решения; при а =2 три решения; при а ϵ(0,2) четыре решения.
Замечание: Заметим, что прямая у=ах «вращается» вокруг начало координат, поэтому этот метод и называется методом «поворота».
Задача 2.(ЕГЭ 2012г). Найти все значения а, при каждом из которых уравнение 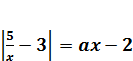 на промежутке (0;+∞) имеет более двух корней.
на промежутке (0;+∞) имеет более двух корней.
Решение. Данное уравнение имеет вид:
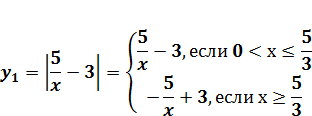
График  состоит частей двух гипербол, а
состоит частей двух гипербол, а  задает семейство линейных функций, графиками которых являются прямые, проходящие через точку А (0;-2).
задает семейство линейных функций, графиками которых являются прямые, проходящие через точку А (0;-2).

Рис.9.
Ответ: 
Занятие 4 (подобие). При решении ряда задач с параметрами с использованием геометрических методов, получаем семейство геометрических фигур, «подобных» друг другу.
Задача 1. Найти значение параметра а, при которых система уравнений  имеет ровно два решения.
имеет ровно два решения.
Решение.  - окружность с центром в начале координат и с радиусом 1. Уравнение
- окружность с центром в начале координат и с радиусом 1. Уравнение 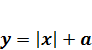 задает семейство «уголков» с вершиной на оси Оу.
задает семейство «уголков» с вершиной на оси Оу.

Рис.10.
«Уголок» касается окружности при а =−√2. По рис.9 видим, что система имеет ровно два решения при а ϵ{−√2 } ∪ (−1; 1).
Ответ: a ϵ {−√2 } ∪ (−1; 1).
Занятие 5 (координатная плоскость а0х). Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах, этот метод один из эффективных методов решения задач с параметрами. Для того чтобы наиболее полно раскрыть возможности этого метода, покажем его применение для основных типов задач.
Задача 1. При каких значениях а уравнение  имеет два корня?
имеет два корня?
Решение. Перейдем к равносильной системе

Эта система на координатной плоскости (х;а) задает кривую, изображенную на рис.11 сплошной линией. Ясно, что все точки этой дуги параболы имеют координаты (х;а), удовлетворяющие исходному уравнению. Поэтому число решений уравнения при каждом фиксированном значении параметра а равно количеству точек пересечения кривой с горизонтальной прямой, соответствующей этому значения параметра.

Рис.11.
Очевидно, при  указанные прямые пересекают график в двух точках, что равносильно исходному уравнению иметь два корня.
указанные прямые пересекают график в двух точках, что равносильно исходному уравнению иметь два корня.
Ответ: 
Задача 2. При каких значениях а уравнение  имеет ровно три корня?
имеет ровно три корня?
Решение. Имеем

График этой совокупности – объединение «уголка» и параболы (рис.12). Очевидно лишь прямая а =-1 пересекает полученное объединение в трех точках.
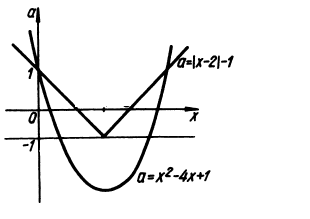
Рис.12.
Ответ. а =-1.
Занятие 6 (координатная плоскость аох неравенства).
Задача 1. Найти все значения а, при которых любое решение неравенства  по модулю не превосходит двух.
по модулю не превосходит двух.
Решение. Перепишем данное неравенство в таком виде:
 . Графики уравнений
. Графики уравнений  и
и  разбивают координатную плоскость (х;а) на четыре области. «Методом интервалов» устанавливаем, что решением исходного неравенства будут заштрихованные области (рис.13). Теперь, если при каком-то фиксированном значении
разбивают координатную плоскость (х;а) на четыре области. «Методом интервалов» устанавливаем, что решением исходного неравенства будут заштрихованные области (рис.13). Теперь, если при каком-то фиксированном значении  прямая
прямая  в пересечении с полученной областью дает лишь точки, абсциссы которых удовлетворяют условию
в пересечении с полученной областью дает лишь точки, абсциссы которых удовлетворяют условию  , то
, то  - одно из искомых значений параметра. Тогда очевидно, что все а из отрезка АВ нам подходят.
- одно из искомых значений параметра. Тогда очевидно, что все а из отрезка АВ нам подходят.

Рис.13.
Ответ:  .
.
Задача 2. Решить неравенство  .
.
Решение. Данная совокупность двух систем равносильна данному неравенству.

Далее, при объединении графических образов каждой из этих систем следует учесть, что прямая  касается параболы
касается параболы 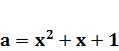 в точке (-1;1).
в точке (-1;1).

Рис.14.
Итак, на рис.14 изображены все решения исходного неравенства. Горизонтальные прямые, пересекающие это множество, пересекают его по отрезку (за исключением одной прямой  ). Очевидно абсциссы всех точек этого отрезка и будут решениями данного неравенства. Для получения ответа осталось выразить х через а в уравнении
). Очевидно абсциссы всех точек этого отрезка и будут решениями данного неравенства. Для получения ответа осталось выразить х через а в уравнении  . При
. При  имеем
имеем  .
.
Ответ: 
Вывод: Геометрический метод нагляден, позволяет сэкономить время, увидеть и рассмотреть все возможные варианты решений, способствует не только выработке умений и закреплению навыков решения задач, но и формированию устойчивого интереса к предмету.
Аналитический способ - это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра.
По мнению большинства авторов различных сборников по решению задач с параметром, аналитический способ решения задач есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Занятие 7 (линейные уравнения и неравенства).
Самыми простыми уравнениями с параметрами является линейные уравнения с одним неизвестным. Это уравнения вида

где а и b – некоторые числа. Число а называется коэффициентом, b – свободным членом уравнения.
Основные задачи, которые мы будем решать применительно к уравнению, является стандартными для всех уравнений с параметрами.
Для решений неравенств нам понадобятся основные свойства неравенств.
Задача 1. При всех а решить уравнение

Решение. Перенесем все члены, содержащие х, в левую часть, а не содержащие в правую. Имеем
 или
или  .
.
Теперь очевидно, исходное уравнение – линейное. Заметим, что мы не можем сразу разделить обе части уравнения на  и сказать, что
и сказать, что  не имеет смысла.
не имеет смысла.
Поэтому, необходимо отдельно рассмотреть случай, когда  .
.
Случай 1.  , т.е
, т.е 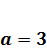 или
или  .
.
а) При 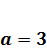 уравнение принимает вид 0* х =0. Это уравнение имеет решениями все действительные числа.
уравнение принимает вид 0* х =0. Это уравнение имеет решениями все действительные числа.
б) При  уравнение имеет вид 0*х=-6, которое, очевидно, решений не имеет.
уравнение имеет вид 0*х=-6, которое, очевидно, решений не имеет.
Случай 2.  , т.е. а≠3 и а≠-3. Тогда из уравнения получаем
, т.е. а≠3 и а≠-3. Тогда из уравнения получаем  .
.
Ответ: при  решений нет; при
решений нет; при 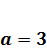 решениями являются все хϵ R; при а≠3 и а≠-3 уравнение имеет одно решение
решениями являются все хϵ R; при а≠3 и а≠-3 уравнение имеет одно решение 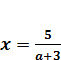 .
.
Замечание. При решении системы двух уравнений с одним неизвестным совсем не обязательно решать оба уравнения и затем выбирать одинаковые корни обоих уравнений в качестве решений системы. Можно решить одно из уравнений и, подставив полученные значения во второе, проверить, удовлетворяют ли они ему, что зачастую проще.
Главные выводы при исследовании линейных уравнений с параметрами:
1. Имеет решения хϵR при  ;
;
2. Не имеет решений при  ;
;
3. Имеет единственное решение  при
при  .
.
Желательно эти выводы запомнить, чтобы при решении более сложных задач сразу пользоваться готовыми результатами, а не выводить их каждый раз заново.
Задача 2. При всех значениях параметра а решить неравенство

Если бы мы решали уравнение  мы бы рассматривали два случая:
мы бы рассматривали два случая:  и
и  . При решении же неравенства нам придется рассмотреть три случая:
. При решении же неравенства нам придется рассмотреть три случая: 
 и
и 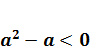 . Это связано с тем, что свойства неравенств при делении на положительные и на отрицательные числа разные. А нам придется в этом примере делить на
. Это связано с тем, что свойства неравенств при делении на положительные и на отрицательные числа разные. А нам придется в этом примере делить на  .
.
Решение.
Случай 1.  , т.е. а=0 или а=1.
, т.е. а=0 или а=1.
а) а=0. Тогда неравенство имеет вид 0*х<3, которое, очевидно, выполняется при любых х.
в) а=1. Тогда имеем неравенство 0*х<0, которое не выполняется ни при каких х.
Случай 2.  . Тогда, разделив обе части неравенства на
. Тогда, разделив обе части неравенства на  , получаем
, получаем

Следовательно, решениями неравенства в этом случае будут  .
.
Случай 3. 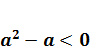 ↔
↔  Тогда, разделив на
Тогда, разделив на  и поменяв знак неравенства, получаем
и поменяв знак неравенства, получаем
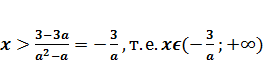 .
.
Ответ: при а =0 решениями являются х ϵ R; при а =1 решений нет; при  решениями являются
решениями являются  ; при
; при  решениями являются
решениями являются  .
.
Занятие 8 (уравнения и неравенства с модулем).
Задача 1. При каких а уравнение

имеет не менее четырех различных решений, являющихся целыми числами?
Решение. Очевидно, что при а =0 это уравнение имеет вид

и, как нетрудно установить, его решением служит отрезок [-1;0], содержащий лишь два целых числа, а не четыре, как требует условие. Поэтому для решения задачи достаточно исследовать полученное уравнение.
Мы можем раскрыть модули, рассмотрев необходимые случаи. Но мы покажем другое решение, наиболее рациональное.
Вначале заметим, что  , так как левая часть уравнения неотрицательна. Теперь воспользуемся геометрической интерпретацией модуля. Тогда искомое значения переменной х – это координаты точек числовой прямой, у которых сумма расстояний до точек -
, так как левая часть уравнения неотрицательна. Теперь воспользуемся геометрической интерпретацией модуля. Тогда искомое значения переменной х – это координаты точек числовой прямой, у которых сумма расстояний до точек -  и -1 равна
и -1 равна  , т.е длина отрезка [-1;
, т.е длина отрезка [-1;  ]. Следовательно, каждая точка отрезка [-1;
]. Следовательно, каждая точка отрезка [-1;  ], и только она, есть решение уравнения. Для завершения решения достаточно потребовать, чтобы отрезок [-1;
], и только она, есть решение уравнения. Для завершения решения достаточно потребовать, чтобы отрезок [-1;  ] содержал четыре целых числа. Ясно, что этими числами будут -1,0,1,2. Отсюда получаем условие 2 ≤
] содержал четыре целых числа. Ясно, что этими числами будут -1,0,1,2. Отсюда получаем условие 2 ≤  или а ≤
или а ≤ 
Ответ: а ≤ 
Задача 2. При всех a решите неравенство
|x + a| > a.
Решение. Отметим, что при замене параметра a на произвольное число получается вполне стандартная задача. Поэтому можно применить метод интервалов для модулей. Сначала отметим, что при a < 0 это неравенство, очевидно, верное (так как модуль числа — неотрицательная величина) при любом a. Поэтому получаем часть ответа: если a < 0, то x ∈ (−∞; +∞).
Если a = 0, то | x | > 0 и x ∈ (−∞; 0) ∪ (0; +∞).
Если a > 0, то следует рассмотреть два случая: x < − a и x ≥ − a.
В первом из них исходное неравенство равносильно следующему:
− x − a > a ↔ − x > 2 a ↔ x < −2 a.
Так как a > 0, число −2 a меньше, чем − a. Поэтому
x ∈ (−∞; −2 a) ⊂ (−∞; − a), и пересечение этих областей совпадает с (−∞; −2 a).
Во втором случае, т. е. при x + a > 0, получаем x + a > a, x > 0, x ∈ (0; +∞). Так как −a < 0, множество [− a; +∞) содержит множество (0; +∞), и их пересечение равно (0; +∞). Поэтому при a > 0 решением неравенства будет (−∞; −2 a) ∪ (0; +∞).
Объединим части ответа: если a < 0, то x ∈ (−∞; +∞); если a = 0, то x ∈ (−∞; 0) ∪ (0; +∞); если a > 0, то x ∈ (−∞; −2 a) ∪ (0; +∞).
Заметим, что если a = 0, то −2 a = 0, поэтому последние две части ответа можно объединить так: если a > 0, то x ∈ (−∞; −2 a)∪(0; +∞).
Ответ. Если a < 0, то x ∈ (−∞; +∞); если a > 0, то x ∈ (−∞; −2 a) ∪ (0; +∞).
Замечание. В задачах с модулем полезны неравенства

Занятие 9 (квадратные уравнения).
Мы рассмотрим уравнения вида  . При а =0 это уравнение линейное, при а ≠0 – квадратное. Число различных задач с параметрами для квадратных уравнений больше, чем для линейных, и они намного разнообразнее. Рассмотрим задачи.
. При а =0 это уравнение линейное, при а ≠0 – квадратное. Число различных задач с параметрами для квадратных уравнений больше, чем для линейных, и они намного разнообразнее. Рассмотрим задачи.
Задача 1. При каких а уравнение

имеет один корень; два корня; ни одного корня.
Решение. Данное уравнение – квадратное. Оно имеет один корень, когда дискриминант равен 0. Имеем:

Итак, при а =1 и а =6 уравнение имеет один корень. Исходное уравнение имеет два корня, если D>0. Имеем,  . Решая это неравенство, получаем а ϵ (-∞;1)ᴗ(6;+∞). И квадратное уравнение не имеет корней, если D<0. Имеем,
. Решая это неравенство, получаем а ϵ (-∞;1)ᴗ(6;+∞). И квадратное уравнение не имеет корней, если D<0. Имеем,  . Решая последнее неравенство, получаем а ϵ(1;6).
. Решая последнее неравенство, получаем а ϵ(1;6).
Ответ: при а=1 и а=6 одно решение; при а ϵ(1;6) решений нет; при а ϵ (-∞;1)ᴗ(6;+∞) два решения.
Задача 2. При всех а решить уравнение

Решение. Случай 1.  =0↔а=1 или -1. В этом случае уравнение – линейное.
=0↔а=1 или -1. В этом случае уравнение – линейное.
а) При а=1 имеем  .
.
в) При а=-1 имеем  .
.
Случай 2. а≠1, а≠-1. Тогда исходное уравнение квадратное. Имеем, D=  .
.
a) Если D<0↔  ↔аϵ(
↔аϵ( ), то решений нет.
), то решений нет.
b) Если D>0↔  ↔аϵ(-∞;(
↔аϵ(-∞;( )ᴗ(
)ᴗ( ), то с учетом того, что а≠±1, уравнение имеет два решения
), то с учетом того, что а≠±1, уравнение имеет два решения  и
и 
c) Если D=0↔ 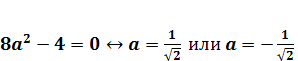 уравнение имеет один корень:
уравнение имеет один корень:
1. При  уравнение принимает вид
уравнение принимает вид  . Его единственный корень которого
. Его единственный корень которого  .
.
2. При 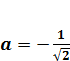 уравнение имеет вид
уравнение имеет вид  . Его единственный корень которого
. Его единственный корень которого 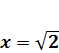 .
.
Ответ: при аϵ( ) решений нет; при а=1 решение х
) решений нет; при а=1 решение х  ; при а=-1 решение х=
; при а=-1 решение х=  ; при
; при  решение
решение  ; при
; при 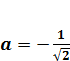 решение
решение 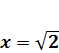 ; при
; при  решения
решения  .
.
Замечание. Это занятие является одним из самых важных, потому что большинство задач сводятся к исследованию квадратного трехчлена. Поэтому желательно научиться свободно решать эти задачи. И, последнее, при исследовании всех квадратных уравнений вида ax 2+ bx+c=0 обязательно рассматривать случай а =0.
Занятие 10 (квадратные неравенства).
Задача 1. При каких а неравенство

выполняется при всех х <2.
Решение этой задачи сведется к поиску нужного нам расположения параболы относительно точки х =2.
Решение. Нарисуем график  . В зависимости от а он может быть выше оси Ох, касаться ее и иметь с ней две общие точки. При этом, если парабола
. В зависимости от а он может быть выше оси Ох, касаться ее и иметь с ней две общие точки. При этом, если парабола  имеет общие точки
имеет общие точки  и
и  с осью Ох, то они могу быть слева от точки х =2, справа, и точка х =2 может быть между
с осью Ох, то они могу быть слева от точки х =2, справа, и точка х =2 может быть между  и
и  .
.
Случай 1. Если график  находится выше оси Ох, то очевидно, что у>0 при всех хϵR, и в частности, при х <2. А как мы уже говорили, условием того, что график находится выше оси Ох, является условие D<0. Имеем D=
находится выше оси Ох, то очевидно, что у>0 при всех хϵR, и в частности, при х <2. А как мы уже говорили, условием того, что график находится выше оси Ох, является условие D<0. Имеем D=  Таким образом, часть решений мы нашли.
Таким образом, часть решений мы нашли.
Случай 2. Парабола пересекает ось Ох в двух точках. Чтобы увидеть все возможные варианты расположения такой параболы относительно точки 2, лучше всего представить себе, что парабола «движется слева направо» вдоль оси Ох. Сначала обе точки пересечения находятся левее точки 2, затем правая ветвь проходит через точку 2, затем точка становится между точками пересечения, потом левая ветвь проходит через точку 2, и, наконец, обе точки пересечения становятся правее точки 2. Мы видим пять возможных вариантов расположения парабол.
Очевидно, что нам первый вариант не подходит, т.к. на промежутке [  ] значение у≤0. Аналогично нам не подходят и второй, третий вариант. А вот четвертый вариант нам подходит, т.к. при всех х <2 значение у >0. Нам так же подходит и пятый вариант, хотя в самой точке 2 имеем у (2)=0, но при всех х <2 значение у >0.
] значение у≤0. Аналогично нам не подходят и второй, третий вариант. А вот четвертый вариант нам подходит, т.к. при всех х <2 значение у >0. Нам так же подходит и пятый вариант, хотя в самой точке 2 имеем у (2)=0, но при всех х <2 значение у >0.
Парабола в пятом варианте характеризуется тем, что ее корни находятся правее точки 2. А это имеет место, если выполняются условия:
1. 
Парабола в четвертом варианте характеризуется тем, что меньший из ее корней 2. А это выполняется тогда и только тогда, когда
2. 
Случай 3. Рассмотрим теперь касания параболы оси Ох. Возможны три различных варианта расположения такой параболы относительно точки 2. Вершина параболы находится левее точки 2; в точке 2; правее точки 2. Рассуждая, как и ранее, видим, что парабола первого варианта не удовлетворяет условиям задачи, а варианты два и три удовлетворяют.
В итоге получаем две системы:
3.  и 4.
и 4. 
Решив полученные системы 1-4, мы найдем все значения а, удовлетворяющие условиям задачи.
Но можно все эти четыре системы объединить в одну систему, которая содержит решения всех четырех систем и только их:
 .
.
Вспоминая случай 1, получаем окончательный ответ.
Ответ: а ϵ 
Замечание. Если еще раз посмотреть на решение этой задачи, то легко видеть, что нам подошли только параболы, которые находятся над осью Ох (в этом случае неравенство выполнялось вообще при всех х) и параболы, которые пересекали ось Ох вне множества х <2 (в крайнем случае, проходили через саму точку х =2). Примерно такая же картина будет иметь место при исследовании всех неравенств этого типа.
Вывод. Аналитический метод является не только самостоятельным методом решения задач, но и обязательной составной частью всех остальных методов. Основной частью аналитического метода решения задач является метод равносильных преобразований. Предлагаемый подход к решению уравнений и неравенств с параметрами, их систем или совокупностей основан на замене одного математического высказывания другим равносильным математическим высказываниям. В аналитическом методе решения задач чаще всего используется прием дробления – разделение условия задач на совокупность более простых условий.
2.5 Апробация элективного курса «Задачи с параметрами»
Педагогический эксперимент проводился в 2015 году в 10-ых классах гимназии №45 г. В качестве основной экспериментальной базы был выбран 10 «Б» класс. Изучение курса предполагает формирование у учащегося интереса к предмету, развитие их математических способностей, подготовку к ЕГЭ, развивать исследовательскую и познавательную деятельность учащегося.
Несмотря на то, что элективный курс – это курс по выбору, связанный, прежде всего, с удовлетворением индивидуальных образовательных интересов, потребностей и склонностей каждого школьника, на занятиях присутствовал почти весь класс, так как занятия проводились в рамках времени, отведенного на факультативы, которые в данной школе проводятся в обязательном порядке.
Некоторые школьники уже выбрали математику в качестве основы продолжения своего образования. Они были заинтересованы в рассмотрении предложенных тем, выполнении заданий. Так как на занятиях присутствовал весь класс в обязательном порядке, то среди учащихся были те, у которых нет потребностей и способностей к изучению математики, вследствие чего предложенные задания оказались непосильными и не вызвавшими интереса.
Разработка курса проводилась в III этапа:
Первый этап состоял в получении данных, с помощью тестирование, которые позволили выявить уровень знаний и умений учащихся, необходимых для усвоения содержания элективных курсов.
На втором этапе осуществлялась разработка экспериментальных материалов.
Третий, завершающий этап работы, состоял в проверке гипотезы исследования. Выяснить, действительно ли разработанные нами элективные курсы и методика их реализации способствуют повышению качества знаний и интенсивности деятельности учащихся.
В соответствии с указанными этапами остановимся на описании результатов экспериментальной работы.
Первый этап экспериментальной работы носил констатирующий характер. На этом этапе проводилось тестирование. В этом тестирование приняли участие 10 «А» и 10 «Б» классы. Целью данного этапа исследования явилось определение знаний и умений в решение задач с параметрами.
Учащимся предлагалось решить 4 задачи с параметрами.
1.При всех, а решить уравнение (2а-4)х=3а+1.
2.При каких значениях, а парабола  касается оси х.
касается оси х.
3.При каких значениях параметра, а уравнение имеет решение  .
.
4. Найдите все значения параметра а, при которых неравенство  не имеет решений на отрезке [-1;2].
не имеет решений на отрезке [-1;2].
Результаты решения представлены в таблице.
Таблица 1.
| oценки | описание | 10 «А» (27 чел) | 10 «Б» (25 чел) |
| Справились со всеми задачами. | 0 (0%) | 0 (0%) | |
| Не справились с одной, задачей. | 5 (18%) | 4 (16%) | |
| Не справились с двумя задачами. | 10 (37%) | 8 (32%) | |
| Не справились от трех и больше задачами. | 12 (45%) | 13(52%) |
Второй этап экспериментальной работы носил поисковый характер. Этот этап был связан с уточнением тематики элективных курсов, разработкой их содержания и соответствующих методических материалов.
Разрабатываемые методические материалы включили в себя содержание элективных курсов, систему организации и методическое обеспечение и соответствующие рекомендации учителям математики в процессе реализации каждого курса.
Поэтому на данном этапе исследования осуществлялся отбор содержания и методики реализации элективных курсов в соответствии с принципами, указанными в первой главе диссертации.
Наблюдения за ходом внедрения элективных курсов, результатами их выполнения давали возможность для уточнения, улучшения содержания элективных курсов и методических рекомендаций по их использованию.
Результаты второго этапа экспериментальной работы дали возможность выделить тематику целесообразных элективных курсов, получить содержание и методику их реализации.
Третий, завершающий этап экспериментального исследования, носил обучающий (формирующий) характер и преследовал цель - проверить гипотезу исследования.
Для проведения эксперимента были отобраны 2 класса – 10 «А» и 10 «Б». 10 «Б» класс был экспериментальный, в нем проводились элективные курсы, а в 10 «А» классе не проводились элективные курсы.
В экспериментальном классе элективные курсы были организованы на базе наших разработок в объеме 2 часа в неделю.
Общее количество учащихся в экспериментальном классе составило 25 и во втором классе -27.
С целью сравнения первоначального уровня знаний учащихся и сформированности у них умений решать математические задачи осуществлялась проверка интенсивности деятельности и выявление индивидуальных особенностей учащихся.
Интенсивность деятельности учащихся проверялась в ходе наблюдения за их временными затратами при решении определенных задач.
Для этого были выделены следующие этапы деятельности учащихся:
1. Планирование работы;
2. Составление математической модели (если задача текстовая или прикладная).
3. Составление алгоритма решения задачи.
4. Реализация алгоритма решения.
5. Анализ результатов.
Больше всего времени учащиеся затрачивают на планирование своей деятельности. Этот факт отмечен в обеих группах. В экспериментальном классе у учащихся вызвали некоторые затруднения анализ результатов.
Результаты во втором классе несколько выше, чем в экспериментальном. Это объясняется тем, что во второй класс вошли учащиеся, у которых были выше баллы на ГИА, чем у экспериментального класса.
Для выявления индивидуальных особенностей учащихся пользовались методом экспертных оценок. В качестве экспертов выступали учителя математических дисциплин и классные руководители. Им было предложено заполнить карту оценки характеристики интеллекта учащегося. Результаты оценки отражены в таблице.
Таблица 2.
|
Эти данные указывают на достаточно высокий потенциал учащихся.
На основе выше изложенного можно сделать следующие выводы: 1. Учащиеся экспериментального класса имеют достаточно высокий интеллектуальный уровень, что подтверждает результаты констатирующего эксперимента о возможности усвоения содержания предлагаемых элективных курсов. Однако, как показали наблюдения, учащиеся экспериментальной группы имеют несколько низкие показатели индивидуальных особенностей и уровня успеваемости.
2. Среднее значение темпа работы и характеристика интеллекта в обеих группах показывают на возможность дальнейшего сравнения качества знаний.
На этапе формирующего эксперимента осуществлялись внедрение и проверка эффективности предлагаемых курсов.
Анализ результатов усвоения у учащихся:
Таблица 3.
| оценки | описание | 10 «А» (27 чел) | 10 «Б» (25 чел) |
| Справились со всеми задачами. | 0 (0%) | 2 (8%) | |
| Не справились с одной, задачей. | 6 (22%) | 8 (32%) | |
| Не справились с двумя задачами. | 12 (44%) | 13 (52%) | |
| Не справились от трех и больше задачами. | 9 (34%) | 2(8%) |
Во время проведения занятий было выявлено, что ученики усвоили
тему из школьного курса алгебры и имеют представление о том, что такое параметр. Но при выполнении предложенных заданий у школьников возникали затруднения, так как задачи требовали исследовательских навыков, логического мышления, что, как оказалось, у них развито слабо. Это говорит о том, что школьный курс ограничен и не позволяет рассматривать задачи, требующие не только действий по алгоритму.
Самостоятельный поиск решения оказался для учеников сложным, но все же позволил школьникам проявить свои способности, заставил задуматься над задачами.
У некоторых учеников есть склонность к изучению математики, но базовый курс математики не создает условий для подтверждения выбранной траектории обучения в соответствии со склонностями, способностями и потребностями школьника и развития этих способностей.
На основе полученных данных формирующего эксперимента можно сделать выводы:
1. Предлагаемые элективные курсы могут быть использованы в подготовке учащихся.
2. Предлагаемая методика является доступной для понимания учащимися старшего звена школы.
3. Дифференцированный подход к учащимся позволил повысить интенсивность их деятельности и добиться на различных этапах однородных результатов.
4. Результаты проведённого исследования указывают на эффективность предлагаемой методики.
Согласно выдвинутой гипотезе нашего исследования в результате внедрения элективных курсов в учебный процесс общеобразовательного учебного заведения повышается эффективность учебного процесса, мотивация и интерес учащихся к знаниям в области математики.
Заключение
В данной работе была рассмотрена проблема подготовки школьников к сдаче ЕГЭ и создание элективного курса «Задачи с параметрам».
В соответствии с целью данной работы и поставленными задачами, а также в результате проведенного теоретического и экспериментального исследования получены следующие выводы и результаты:
Определена структура тестов, которая послужила основой при подборе тем элективного курса;
разработано содержание элективного курса;
подобраны формы проведения элективных курсов;
разработаны методические рекомендации и проведения элективного курса.
Элективные курсы дают учащимся не только необходимые для поступления знания, умения, навыки, но и позволяют систематизировать самоподготовку учащихся, способствуют развитию у учеников логического мышления, математической речи, навыков самоконтроля и самооценки.
Разработанный элективный курс может быть использован учителями математики при подготовке к ЕГЭ. В нем систематизирован теоретический и дидактический материал, отвечающий принципу последовательного нарастания сложности.
Date: 2016-07-22; view: 440; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |