
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методы описания процессов в системах управления
Анализ динамики процессов составляет основу решения задач управления в предметных областях широкого класса. Целью данного раздела является рассмотрение базовых моделей динамики процессов, используемых при решении задач управления.
Детализованное во времени описание функциональных процессов может быть представлено, например, следующим рекуррентным выражением
 (10)
(10)
Здесь текущее значение выходного процесса 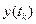 на момент времени
на момент времени  определяется множеством предыдущих значений самого процесса
определяется множеством предыдущих значений самого процесса  , множеством предыдущих значений входного процесса
, множеством предыдущих значений входного процесса  и текущим моментом времени
и текущим моментом времени  . Отображение
. Отображение  представляет в общем случае теоретико-множественную функцию многих переменных. Само выражение (10) определяет рекуррентный вычислительный процесс определения неизвестных значений выходного процесса
представляет в общем случае теоретико-множественную функцию многих переменных. Само выражение (10) определяет рекуррентный вычислительный процесс определения неизвестных значений выходного процесса 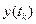 , исходя из известных предыдущих значений самого процесса
, исходя из известных предыдущих значений самого процесса  , известных предыдущих значений входного процесса
, известных предыдущих значений входного процесса  и текущего момента времени
и текущего момента времени  .
.
Обратим внимание, что функция (10), определяет значения выходного процесса, исходя из знания только предыдущих значений наблюдаемых процессов. Это свойство отражает реальное свойство физических систем – строгой неупреждаемости действий во времени. Действия, проходящие в физических системах, всегда задерживаются во времени вследствие инерционности, присущей реальным физическим процессам. Поэтому ограничения
 ,
,  , (11)
, (11)
наложенные на рекуррентный процесс (10), являются условиями его физической реализуемости. Связи процессов, определяемые рекуррентным выражением (10) при условиях (11) являются связями с запаздывающим действием (инерционные связи).
В идеализированных случаях возможно выполнение нестрогих условий
 ,
,  . (12)
. (12)
Действия, удовлетворяющие условиям (12), являются неупреждающими. Подобные действия проявляются без запаздывания, мгновенно. Поэтому в данном случае связи процессов являются связями с безынерционным действием (безынерционные связи).
В общем случае с математической точки зрения рекуррентное соотношение (9) может быть определено и при условиях
 ,
,  . (13)
. (13)
Такие действия являются упреждающими и физически нереализуемыми. Однако если удается тем или иным физически реализуемым способом получать прогноз будущих значений процессов  ,
,  , то соответствующее рекуррентное соотношение будет определять связи процессов с прогнозируемым действием (прогнозирующие связи).
, то соответствующее рекуррентное соотношение будет определять связи процессов с прогнозируемым действием (прогнозирующие связи).
Далее, связь процессов называется статической, если она определяется для статических процессов, постоянных во времени:
 ,
,  . (14)
. (14)
В этом случае рекуррентное соотношение (9) вырождается в функцию
 (15)
(15)
Функция (15) определяет статическую характеристику связи. В общем случае связи носят динамический характер. При этом описание динамических характеристик связей может быть осуществлено на основе разнообразных представлений. Одним из способов представления динамических характеристик связей является использование рекуррентных соотношений вида (10).
При использовании рекуррентных соотношений вида (10) последовательности значений процессов
 ,
,  (16)
(16)
определяют предысторию рассматриваемой динамической связи процессов относительно текущего момента времени  . Значение выходного процесса на текущий момент времени зависит от его предыстории. При этом величина интервала времени предыстории
. Значение выходного процесса на текущий момент времени зависит от его предыстории. При этом величина интервала времени предыстории 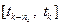 , из которого значения (16) входного процесса
, из которого значения (16) входного процесса  учитываются в динамической характеристике связи (10), определяет память динамической связи. Соответственно число
учитываются в динамической характеристике связи (10), определяет память динамической связи. Соответственно число  предыдущих значений выходного процесса (16), которые учитываются динамической характеристикой связи (10), определяет порядок динамической связи. В общем случае понятия памяти и порядка динамической связи определяются в зависимости от конкретного вида представлений динамических характеристик связей процессов.
предыдущих значений выходного процесса (16), которые учитываются динамической характеристикой связи (10), определяет порядок динамической связи. В общем случае понятия памяти и порядка динамической связи определяются в зависимости от конкретного вида представлений динамических характеристик связей процессов.
Для начала рекуррентного вычислительного процесса (10) в начальный момент времени  необходимо знать начальные условия, которые в данном случае определяются предысторией выходного процесса
необходимо знать начальные условия, которые в данном случае определяются предысторией выходного процесса
 . (17)
. (17)
Из выражения (17) следует, что число начальных условий для однозначного определения выходного динамического процесса по входному процессу определяется порядком динамической связи процессов.
В общем случае однозначное определение выходных процессов основывается на использовании понятия состояния динамической системы. Под состоянием динамической системы понимается совокупность исходной информации о процессах в системе на начальный момент времени  , достаточная для однозначного определения выходного процесса системы по входному процессу в последующие моменты времени
, достаточная для однозначного определения выходного процесса системы по входному процессу в последующие моменты времени  . В соответствии с данным определением предыстория выходного процесса (17) для случая описания динамических связей рекуррентным соотношением (10) играет роль состояния динамической связи. Для других форм описания динамических связей в роли состояния могут быть использованы иные характеристики процессов. Например, при описании связей непрерывных процессов дифференциальными уравнениями в роли состояния используются начальные значения производных выходного процесса.
. В соответствии с данным определением предыстория выходного процесса (17) для случая описания динамических связей рекуррентным соотношением (10) играет роль состояния динамической связи. Для других форм описания динамических связей в роли состояния могут быть использованы иные характеристики процессов. Например, при описании связей непрерывных процессов дифференциальными уравнениями в роли состояния используются начальные значения производных выходного процесса.
Рассмотрим процессы, происходящие в контурах обратной связи. Типовая структура контура обратной связи изображена на рис. 4.2.1.
 |
Структурная схема связей процессов (рис. 4.1.1) служит основой для построения системы уравнений, описывающих процессы в рассматриваемом контуре обратной связи. При этом можно дать концептуальную схему системы уравнений связей процессов
 (18)
(18)
Соответственно, для случая представления процессов в форме развертки во времени с учетом рекуррентного соотношения (10) вид системы уравнений будет следующий
 (20)
(20)
Решение систем уравнений (19), (20) может быть выполнено соответствующими вычислительными методами.
На решения систем уравнений (19), (20) существенное влияние оказывает характер обратной связи в контуре (рис. 4.2.1). Обратная связь считается положительной (формально), если в узле обратной связи, описываемым уравнениями (18 а), (19 а), (20 а), осуществляется формальная операция сложения процессов  ,
,  . Соответственно, обратная связь считается отрицательной (формально), если в указанном узле осуществляется формальная операция вычитания процесса
. Соответственно, обратная связь считается отрицательной (формально), если в указанном узле осуществляется формальная операция вычитания процесса  из процесса
из процесса  . В действительности процессы, последовательно проходя по контуру обратной связи, могут менять свой знак на противоположный. В этом случае обратная связь, формально положительная с точки зрения операции в узле обратной связи, фактически становится отрицательной, и наоборот, формально отрицательная обратная связь становится фактически положительной. Данные особенности обратных связей необходимо иметь в виду при рассмотрении процессов в контурах обратной связи.
. В действительности процессы, последовательно проходя по контуру обратной связи, могут менять свой знак на противоположный. В этом случае обратная связь, формально положительная с точки зрения операции в узле обратной связи, фактически становится отрицательной, и наоборот, формально отрицательная обратная связь становится фактически положительной. Данные особенности обратных связей необходимо иметь в виду при рассмотрении процессов в контурах обратной связи.
___________________________________
Остановимся более подробно на характере процессов,которые могут происходить в динамических системах.
Характер процессов, происходящих в динамических системах, может быть самым разнообразным. Мы остановимся на некоторых типовых наиболее часто встречающихся видах процессов. К таким процессам можно отнести процессы экспоненциального роста, затухающие процессы, колебательные и их комбинации.
Так, процессы в контуре с положительной обратной связью во многих случаях характеризуются экспоненциальным ростом. Это связано с тем, что процессы, последовательно преобразуясь в контуре с положительной обратной связью, циклически усиливаются пропорционально своей величине. Это наглядно можно видеть на простом численном примере.
Экспоненциальная функция  в общем случае является решением дифференциального уравнения
в общем случае является решением дифференциального уравнения
 , (21)
, (21)
которое выступает как порождающее уравнение процесса экспоненциального роста.
В дискретном варианте, который можно получить, например, на основе явного метода Эйлера интегрирования дифференциальных уравнений[1], уравнение (21) имеет вид
 (22)
(22)
Из соотношений (22) следует, что величина  . Поэтому решение уравнения (22) определяет процесс экспоненциального роста.
. Поэтому решение уравнения (22) определяет процесс экспоненциального роста.
Отрицательные обратные связи способствуют стабилизации процессов. Поэтому контурам с отрицательной обратной связью присущи затухающие процессы.
Так, затухающие процессы во многих случаях могут быть представлены в виде затухающей экспоненты  . Данной экспоненте соответствует дифференциальное уравнение
. Данной экспоненте соответствует дифференциальное уравнение
 , (23)
, (23)
В дискретном варианте, который можно получить, например, на основе неявного метода Эйлера интегрирования дифференциальных уравнений, уравнение (23) имеет вид
 (24)
(24)
Из соотношений (22) следует, что величина  . Поэтому решение уравнения (24) определяет процесс экспоненциального затухания.
. Поэтому решение уравнения (24) определяет процесс экспоненциального затухания.
Типовыми для контуров обратной связи являются колебательные процессы.
Так, колебательный процесс:
 , (25)
, (25)
является решением дифференциального уравнения
 , (26)
, (26)
где  ‑ круговая частота колебаний.
‑ круговая частота колебаний.
Порождающее дифференциальное уравнение для процесса (25) может быть представлено также в полярной системе координат.
В полярной системе координат процесс (25) представляется в виде
 (27)
(27)
Здесь  ‑ длина полярного радиуса, описывающего траекторию процесса,
‑ длина полярного радиуса, описывающего траекторию процесса,  ‑ угол между полярной осью и полярным радиусом. Связь между представлением процесса (25) и представлением (27) определяется формулами
‑ угол между полярной осью и полярным радиусом. Связь между представлением процесса (25) и представлением (27) определяется формулами
 ,
,  ,
,  .
.
В пространстве состояний уравнение (26) принимает вид
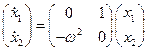 , (28)
, (28)
 ; (29)
; (29)
где  . Здесь выражение (28) представляет собой уравнение перехода состояний
. Здесь выражение (28) представляет собой уравнение перехода состояний  ,
,  ; выражение (29) – выходная функция.
; выражение (29) – выходная функция.
Соответствующие рекуррентные вычислительные выражения имеют вид:
‑ для явного метода Эйлера
 , (30)
, (30)
‑ для неявного метода Эйлера
 , (31)
, (31)
Рассмотрим физическую интерпретацию процесса (25).
Будем полагать, что уравнение (26) описывает движение механической системы. В соответствии с аналитической механикой энергия движения подобной системы состоит из трех составляющих:
‑ кинетической энергии, зависящей от скорости движения,
 ; (32)
; (32)
‑ потенциальной энергии, зависящей от величины координат системы,
 ; (33)
; (33)
‑ рассеянной энергии, определяемой диссипативной функцией
 . (34)
. (34)
Здесь  ‑ масса,
‑ масса,  ,
,  ‑ коэффициенты пропорциональности.
‑ коэффициенты пропорциональности.
Движение соответствующей системы можно описать уравнением в форме Лагранжа
 , (35)
, (35)
где  ‑ действующая потенциальная сила,
‑ действующая потенциальная сила,  ‑ диссипативная сила,
‑ диссипативная сила,  ‑ некоторая внешняя сила.
‑ некоторая внешняя сила.
Если в системе не действуют диссипативные силы, то она является консервативной. В такой системе не происходит рассеивания (диссипации) энергии. Система считается автономной, если на нее не действуют внешние силы.
При условии, что рассматриваемая система является автономной и консервативной, подстановка в уравнение движения системы (35) выражений кинетической (32) и потенциальной (33) энергии приводит к уравнению движения
 . (36)
. (36)
Сравнивая уравнения (26), (36), легко видеть их идентичность при 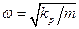 . Таким образом, процесс (25) соответствует движению автономной консервативной системы.
. Таким образом, процесс (25) соответствует движению автономной консервативной системы.
Физика процессов в автономной консервативной системе иллюстрируется графиками на рис. 4.2.2.
 |
Из рассмотрения графиков (рис. 4.2.2) видно, что возникновение колебаний в системе основано на чередовании переходов кинетической энергии в потенциальную и обратно. На максимуме отклонения координаты кинетическая энергия обращается в нулевое значение. Однако здесь достигается максимум потенциальной энергии, которая стремится вернуть координату в положение равновесия. При возврате значения координаты в положение равновесия достигается максимум кинетической энергии и минимум потенциальной. Обладая кинетической энергией, система по инерции проходит положение равновесия и снова достигает максимума отклонения координаты. При этом кинетическая энергия переходит в потенциальную. Так как в консервативной системе отсутствует рассеивание энергии, суммарная энергия системы остается постоянной. Таков физический механизм колебаний.
В случае автономной диссипативной системы подстановка в уравнение движения (35) выражений для различных составляющих энергии системы (32)‑(34) приводит к уравнению движения
 . (37)
. (37)
Решение уравнения (37) имеет вид
 , (38)
, (38)
где
 ,
,  ,
,  . (39)
. (39)
В полярной системе координат уравнение (37) имеет вид
 (40)
(40)
в пространстве состояний –
 , (41)
, (41)
 . (42)
. (42)
Соответствующие рекуррентные вычислительные выражения:
‑ для явного метода Эйлера
 (43)
(43)
‑ для неявного метода Эйлера
 (44)
(44)
Вернемся к рассмотрению выражения (38). Из данного выражения следует, что уравнение (37) определяет затухающие колебания в системе. Численно затухание определяется величиной  ‑ логарифмическим декрементом затухания. При этом в системе наблюдается срыв колебаний при условии
‑ логарифмическим декрементом затухания. При этом в системе наблюдается срыв колебаний при условии  , где
, где  ‑ автоколебания в консервативной системе.
‑ автоколебания в консервативной системе.
Если в системе происходит генерация энергии, то уравнение движения имеет вид
 , (45)
, (45)
где  ‑ коэффициент, характеризующий поставку энергии в систему.
‑ коэффициент, характеризующий поставку энергии в систему.
Решение уравнения (45)
 , (46)
, (46)
где
 ,
,  ,
,  ,
,  . (47)
. (47)
Из выражения (46) следует, что уравнение (45) определяет рост колебаний в системе. Численно рост определяется величиной  ‑ логарифмическим инкрементом роста. При этом в системе также наблюдается срыв колебаний при условии
‑ логарифмическим инкрементом роста. При этом в системе также наблюдается срыв колебаний при условии  .
.
Рост колебаний в системе определяет рост поставляемой энергии
 . (48)
. (48)
В случае если внешний источник энергии имеет ограниченную мощность, величина коэффициента  будет убывать при возрастании величины
будет убывать при возрастании величины  . Другими словами, система будет являться нелинейной относительно коэффициента
. Другими словами, система будет являться нелинейной относительно коэффициента  . Состояние равновесия будет достигнуто при
. Состояние равновесия будет достигнуто при  . При этом в системе установятся автоколебания
. При этом в системе установятся автоколебания
 . (49)
. (49)
В данном случае приток энергии извне компенсирует рассеивание энергии в системе.
Автоколебания (49), установившиеся в нелинейной системе (45), будут устойчивыми. Действительно, если в установившемся состоянии вследствие случайных колебаний энергия в системе уменьшится, то в соответствии с формулой процесса (46) в последующем она возрастет до состояния (49). И наоборот, если энергия в системе возрастет, значение коэффициента  снизится, и система вернется в установившееся состояние.
снизится, и система вернется в установившееся состояние.
Рассмотрим поведение системы (37) под внешним воздействием.
В этом случае дифференциальное уравнение, описывающее динамику процессов в системе, имеет вид
 ; (50)
; (50)
в пространстве состояний –
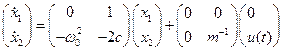 , (51)
, (51)
 . (52)
. (52)
Соответствующие рекуррентные выражения:
‑ для явного метода Эйлера
 (53)
(53)
‑ для неявного метода Эйлера
 (54)
(54)
В рассматриваемом случае процесс на выходе системы будет состоять из двух компонент:
‑ свободной составляющей движения (38), определяемой решением однородного дифференциального уравнения (37);
‑ вынужденной реакцией системы.
Свободная составляющая движения системы была уже рассмотрена выше, см. (39). Поэтому здесь рассмотрим более подробно вынужденную реакцию системы.
Если внешнее воздействие имеет синусоидальный вид
 , (55)
, (55)
то вынужденная реакция системы, движение которой описывает уравнение (50), будет также синусоидальной:
 . (56)
. (56)
Для исследования решений уравнения (50) удобно использовать представления процессов с помощью комплексных чисел. Для данного случая выражения входного и выходного процессов будут иметь вид:
 , (57)
, (57)
 . (58)
. (58)
Подстановка представлений процессов (55)‑(58) в дифференциальное уравнение (50) приводит к выражению данного уравнения в частотной области:
 . (59)
. (59)
Из уравнения (59) следует
 , (60)
, (60)
где
 . (61)
. (61)
Соотношение (60) определяет в частотной области решение уравнения (50). Особенностью указанного частотного подхода является то, что он переводит решение рассматриваемой задачи из дифференциальной формы в алгебраическую. Тем самым решение задачи значительно упрощается.
В классической теории управления функция  называется передаточной функцией. Это связано с информационной трактовкой выражения (60) как преобразования входного сигнала
называется передаточной функцией. Это связано с информационной трактовкой выражения (60) как преобразования входного сигнала  в выходной
в выходной  . Таким образом, передаточная функция
. Таким образом, передаточная функция  характеризует преобразование сигналов, их ориентированную связь
характеризует преобразование сигналов, их ориентированную связь 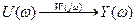 .
.
В общем случае произвольного входного сигнала  вынужденное движение системы может быть получено с использованием преобразования Фурье, которое определяет разложение сигналов в гармоническом базисе. Формулы данного преобразования следующие:
вынужденное движение системы может быть получено с использованием преобразования Фурье, которое определяет разложение сигналов в гармоническом базисе. Формулы данного преобразования следующие:
‑ прямое преобразование Фурье
 ; (62)
; (62)
‑ обратное преобразование Фурье
 . (63)
. (63)
В теории управление широкое распространение получило преобразование Лапласа для сигналов, определенных в положительные моменты времени:
‑ прямое преобразование Лапласа
 ; (64)
; (64)
‑ обратное преобразование Лапласа
 ,
,  . (65)
. (65)
Переменная  здесь является комплексной переменной:
здесь является комплексной переменной:  , где
, где  ‑ абсцисса сходимости преобразования,
‑ абсцисса сходимости преобразования,  ‑ круговая частота. Таким образом, здесь
‑ круговая частота. Таким образом, здесь  . Положительной особенностью преобразования Лапласа является то, что интеграл (64) сходится для более широкого класса функций по сравнению с преобразованием Фурье.
. Положительной особенностью преобразования Лапласа является то, что интеграл (64) сходится для более широкого класса функций по сравнению с преобразованием Фурье.
Для случая преобразования Лапласа решение уравнения (50) имеет вид аналогичный решению (60) для преобразования Фурье:
 , (66)
, (66)
где
 . (67)
. (67)
Передаточные функции систем относительно гармонических воздействий характеризуются амплитудной и фазовой частотными характеристиками:
 =
=  , (68)
, (68)
 ; (69)
; (69)
где  ,
,  ‑ операции взятия вещественной и мнимой частей комплексных чисел соответственно. Физически амплитудная частотная характеристика определяет коэффициент усиления (ослабления) амплитуды гармонических колебаний, при их прохождении через систему. Соответственно, фазовая частотная характеристика определяет соответственно запаздывание (опережение) колебаний по фазе.
‑ операции взятия вещественной и мнимой частей комплексных чисел соответственно. Физически амплитудная частотная характеристика определяет коэффициент усиления (ослабления) амплитуды гармонических колебаний, при их прохождении через систему. Соответственно, фазовая частотная характеристика определяет соответственно запаздывание (опережение) колебаний по фазе.
Для динамической системы, представляемой передаточной функцией (61), амплитудная частотная характеристика имеет вид
 . (70)
. (70)
Из зависимости (70) следует, что максимальное значение амплитудная частотная характеристика имеет на частоте  , которая является частотой резонанса системы (59). Величина амплитудной частотной характеристики на частоте резонанса определяется коэффициентом рассеивания энергии
, которая является частотой резонанса системы (59). Величина амплитудной частотной характеристики на частоте резонанса определяется коэффициентом рассеивания энергии  . При
. При  величина амплитудной частотной характеристики неограниченно возрастает
величина амплитудной частотной характеристики неограниченно возрастает  .
.
Рассмотренная динамическая система, движение которой описывается уравнением (50), относится к классу линейных стационарных систем второго порядка. В общем случае линейные стационарные системы могут иметь произвольный порядок. Движение подобных систем может быть описано как сумма движений элементарных динамических звеньев первого и второго порядков. Математически этот факт показывается следующим образом.
Пусть передаточная функция линейной стационарной динамической системы имеет вид дробно-рациональной функции комплексной переменной:
 ,
,  . (71)
. (71)
Характеристическим уравнением для функции (71) называется уравнение
 . (72)
. (72)
Предположим, что корнями характеристического уравнения (72) являются числа  в общем случае комплексные. Для простоты сначала предположим, что все корни являются простыми. Случай кратных корней будет рассмотрен ниже. Тогда полином, представляющий знаменатель передаточной функции (71), может быть разложен на элементарные сомножители:
в общем случае комплексные. Для простоты сначала предположим, что все корни являются простыми. Случай кратных корней будет рассмотрен ниже. Тогда полином, представляющий знаменатель передаточной функции (71), может быть разложен на элементарные сомножители:
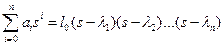 . (73)
. (73)
В случае комплексных корней справедливо правило, что указанные корни являются парными и комплексно сопряженными. Поэтому комплексно сопряженные пары корней можно представить в виде сомножителей второго порядка
 , (74)
, (74)
где  ,
,  .
.
В результате выражение (73) может быть представлено в виде
 . (75)
. (75)
На основе формулы (75) передаточная функция (71) может быть разложена на элементарные динамические звенья:
 , (76)
, (76)
где  ,
,  ,
,  ‑ постоянные коэффициенты, которые определяются из условия равенства левой и правой частей соотношения (76).
‑ постоянные коэффициенты, которые определяются из условия равенства левой и правой частей соотношения (76).
В случае кратных корней соответствующие сомножители  входят в разложение передаточной функции (76) в виде суммы
входят в разложение передаточной функции (76) в виде суммы
 . (77)
. (77)
Формулы свободного движения для элементарных звеньев с кратными корнями также имеют свои особенности. Здесь экспоненциальная составляющая в решениях дифференциального уравнения  -го порядка имеет дополнительно полиномиальную составляющую
-го порядка имеет дополнительно полиномиальную составляющую
 .
.
Физический смысл разложения передаточной функции линейной стационарной системы на элементарные звенья состоит в том, что для сложной динамической системы характерным является наличие целого спектра собственных частот, которые существенно определяют ее динамику. Данные частоты возбуждаются как вследствие ненулевых начальных условий, так и входных воздействий. В итоге общая реакция системы на начальные условия и внешние воздействия представляет собой сумму частных движений, определяемых элементарными динамическими звеньями системы.
___________________________________
Рассмотрим действие контура с отрицательной обратной связью на динамику поведения систем. Отрицательные обратные связи возникают в системах, как естественным путем, так и вводятся искусственно для целенаправленного воздействия на их движение. В последнем случае контуры с отрицательной обратной связью являются контурами управления.
Пример контура управления с отрицательной обратной связью представлен на рис. 4.2.3. Здесь 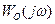 ‑ передаточная функция управляемой динамической системы;
‑ передаточная функция управляемой динамической системы; 
 ‑ коэффициент усиления регулятора;
‑ коэффициент усиления регулятора;  ‑ передаточная функция корректирующего звена регулятора;
‑ передаточная функция корректирующего звена регулятора;  ‑ задающее воздействие,
‑ задающее воздействие,  ‑ управляющее воздействие на динамическую систему;
‑ управляющее воздействие на динамическую систему;  ‑ возмущающее воздействие;
‑ возмущающее воздействие;  ‑ выходная реакция системы;
‑ выходная реакция системы;  ‑ сигнал рассогласования между
‑ сигнал рассогласования между  и
и  .
.
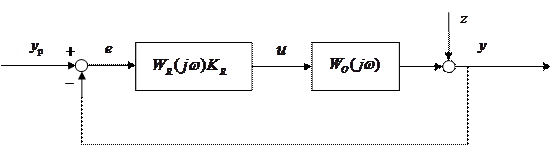 | |||
|
Зависимость выходной реакции системы от внешних воздействий на контур управления в данном случае имеет вид
 , (78)
, (78)
где  ‑ передаточная функция контура по задающему воздействию;
‑ передаточная функция контура по задающему воздействию;
 ‑ передаточная функция контура по возмущающему воздействию.
‑ передаточная функция контура по возмущающему воздействию.
Соответствующие передаточные функции определяются формулами
 , (79)
, (79)
 . (80)
. (80)
В технических системах контур управления на основе выбора значения коэффициента усиления и корректирующего звена регулятора проектируется таким образом, чтобы в рабочем диапазоне частот  выполнялись условия:
выполнялись условия:
 ,
,  ,
,  ,
,  ,
,  . (81)
. (81)
В этом случае управляемая динамическая система отслеживает задающее воздействие:
 ,
,  . (82)
. (82)
При этом влияние возмущающих воздействий должно быть пренебрежимо мало
 ,
,  . (83)
. (83)
Рассчитанный таким образом контур с отрицательной обратной связью становится системой управления. Это – новое качество, которое не было присуще исходной динамической системе. При этом сама динамическая система, которая вошла составной частью в систему управления, стала управляемой.
Качество системы управления должно быть устойчивым. Другими словами система управления не должна терять свое качество, определяемое техническими условиями (81)‑(83), при воздействии возмущений. В рассматриваемом случае это означает, что техническое условие (83) должно выполняться не только для рабочего диапазона частот, но и для частот самого широкого спектра при самых различных спектральных характеристиках помех.
Действие возмущений на выход системы управления можно оценить величиной
 , (84)
, (84)
где  ‑ дисперсия выхода системы;
‑ дисперсия выхода системы;  ‑ спектральная плотность помехи
‑ спектральная плотность помехи  ;
;  ‑ допустимая величина дисперсии выхода системы.
‑ допустимая величина дисперсии выхода системы.
Для выражения (84) справедливо неравенство
 , (85)
, (85)
где  ‑ дисперсия, оценивающая уровень помех в системе:
‑ дисперсия, оценивающая уровень помех в системе:
 .
.
На основе неравенства (85) можно сформулировать требование к запасу устойчивости системы управления при воздействии помех
 . (86)
. (86)
С учетом (80) требование (86) к запасу устойчивости системы управления можно представить в виде
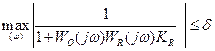 . (87)
. (87)
Показатель (87) называется показателем колебательности системы. Он характеризует резонансные свойства замкнутого контура системы управления по отношению к действующим возмущениям и непосредственно связан с запасами устойчивости системы по частотному критерию устойчивости Найквиста.
Действительно, из неравенства (87) следует
 . (88)
. (88)
Физический смысл неравенства (88) можно наглядно показать с помощью годографа Найквиста (рис. 4.2.4).
 |
Здесь запретная область радиусом  вокруг критической точки (‑1, 0) определяет ограничение для годографа
вокруг критической точки (‑1, 0) определяет ограничение для годографа  частотной характеристики разомкнутого контура системы управления, соответствующее неравенству (88).
частотной характеристики разомкнутого контура системы управления, соответствующее неравенству (88).
Рассмотрим физическую основу потери устойчивости в системах с обратной связью. Обратим внимание, если годограф Найквиста захватывает критическую точку (‑1, 0), это свидетельствует о том, что колебания, проходя по контуру с обратной связью, меняют свой знак на противоположный. При этом формально отрицательная обратная связь становится фактически положительной, что и ведет к потере устойчивости.
____________________________________
Рассмотрим общий подход к описанию процессов в автоматических системах.
Будем полагать, что реализация процесса на выходе автоматической системы  является некоторой функцией от
является некоторой функцией от  и реализации процесса на входе
и реализации процесса на входе  :
:
 . (102)
. (102)
Для автоматических систем выходная функция (102) обладает свойством сочленения. Это означает следующее.
Пусть процесс на входе системы  на интервале времени
на интервале времени  может быть представлен как объединение двух следующих друг за другом составляющих процессов
может быть представлен как объединение двух следующих друг за другом составляющих процессов 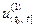 ,
,  на интервалах
на интервалах  ,
,  :
:
 =
= 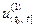 ,
,  =
=  .
.
Тогда выходная функция (102) будет обладать свойством сочленения, если для каждых  и
и  найдется
найдется  , определяемое некоторой функцией
, определяемое некоторой функцией
 ,
,
при котором процесс на выходе

будет составлен из двух следующих друг за другом частных процессов:
 ,
,  .
.
Естественно определить состояние  как начальное состояние
как начальное состояние  , а состояние
, а состояние  ‑ как текущее состояние
‑ как текущее состояние  .
.
Смысл приведенного свойства сочленения состоит в том, что для описания процессов в системе достаточно использовать две функции:
переходную функцию состояния
 , (103)
, (103)
и выходную функцию
 . (104)
. (104)
Уравнения (103), (104) представляют собой уравнения «вход‑выход‑состояние» в интегральной форме. Если продифференцировать уравнение (103) и осуществить предельный переход  в уравнении (104), то в результате можно получить уравнения «вход‑выход‑состояние» в дифференциальной форме
в уравнении (104), то в результате можно получить уравнения «вход‑выход‑состояние» в дифференциальной форме
 , (105)
, (105)
 . (106)
. (106)
Здесь переходная функция состояния  и выходная функция
и выходная функция  уже обычные векторные числовые функции.
уже обычные векторные числовые функции.
Уравнения (105), (106) описывают поведение стационарной нелинейной динамической системы. В нестационарном случае уравнения имеют вид
 , (107)
, (107)
 . (108)
. (108)
Для линейной нестационарной системы уравнения следующие
 , (109)
, (109)
 . (110)
. (110)
В стационарном случае
 , (111)
, (111)
 . (112)
. (112)
Здесь  ,
,  ,
,  ,
,  ‑ матрицы коэффициентов.
‑ матрицы коэффициентов.
В вырожденных случаях, когда входное воздействие  отсутствует, мы имеем автономную систему
отсутствует, мы имеем автономную систему
 , (113)
, (113)
 . (114)
. (114)
Если состояние системы единственно, то получаем обычную статическую векторную функцию
 . (115)
. (115)
Если дискретизировать уравнения (107), (108) на основе какого либо численного метода интегрирования дифференциальных уравнений, то получим дискретный вариант уравнений «вход‑выход‑состояние»
 , (116)
, (116)
 .
.  1, 2, … (117)
1, 2, … (117)
Примерами подобных рекуррентных процедур могут служить ранее рассмотренные рекуррентные выражения для расчета динамических процессов (10), (20), (22), (24), (30), (31), (43), (44), (53), (54).
Аналогичную форму имеют уравнения для автоматов:
‑ автомат Мили
 , (118)
, (118)
 .
.  1, 2, … (119)
1, 2, … (119)
‑ автомат Мура
 , (120)
, (120)
 .
.  1, 2, … (121)
1, 2, … (121)
В частном случае, когда в наличии имеется лишь одно состояние, автомат называется автоматом без памяти и представляет собой логическую схему.
Обратим внимание, что схемы автоматов (108)‑(121) могут быть определены на переменных, которые принимают значения на множествах элементов произвольной природы. Поэтому данная схема носит достаточно общий характер.
Наглядно схему работы автомата можно изобразить с помощью диаграммы перехода состояний, пример которой приведен на рис. 4.2.6. Здесь объекты диаграммы обозначают состояния автомата, дуги ‑ переходы состояний. Каждая дуга помечена упорядоченной парой соответствующих значений входа и выхода автомата. Данный автомат называется конечным, так как число его состояний конечно.
 |
Работа автомата (рис. 4.2.6) может быть описана в табличном виде, как совокупность его действий при наступлении определенных событий на входе.
Таблица действий конечного автомата

| 
| 
|

| 
| 
|
Рассмотренные выше уравнения были получены для частного случая, когда действия динамической системы не распределены в пространстве. При наличии распределения действий в пространстве уравнения «вход‑выход‑состояние» имеют более общий вид
 (t, d) = f (
(t, d) = f ( (t, d); и (t, l); t), (122)
(t, d); и (t, l); t), (122)
y (t, d) = g ( (t, d); и (t, l); t)). (123)
(t, d); и (t, l); t)). (123)
Здесь  (t, d) представляет собой вектор частных производных состояния по временной и пространственным координатам:
(t, d) представляет собой вектор частных производных состояния по временной и пространственным координатам:
 (t, d) =
(t, d) =  ,
,
где [·]T – операция транспонирования матриц (в данном случае матрицы-строки в матрицу-столбец).
Уравнения (122) определяют переходную функцию состояния динамической системы, уравнения (123) – выходную функцию. Указанные функции являются нелинейными и зависят от состояния системы, входных воздействий, времени и пространственных координат. Для однозначного решения системы уравнений (122), (123) необходимо по временной координате задать начальное распределение состояния по исходным границам пространственной области (начальные по времени граничные условия в пространстве)
 (t,
(t,  ) =
) =  (t 0,
(t 0,  ),
), 
 Г 0,
Г 0,
где Г 0 – исходная граница области допустимых изменений пространственных координат.
_________________________________________
Контрольные вопросы
- Какие формализованные модели можно использовать для представления динамических процессов общего вида?
- Какие ограничения, присущие физическим системам, должны отражать формализованные представления динамических систем?
- Какова физическая интерпретация процессов экспоненциального роста и колебательных процессов?
- В чем состоят частотные методы исследования динамики линейных стационарных систем? Дайте их физическую интерпретацию.
- Каким образом можно оценить качество и помехоустойчивость систем управления с обратной связью на основе частотных методов?
- Приведите представления автоматических систем общего вида в пространстве состояний.
[1] Явный метод Эйлера численного интегрирования дифференциального уравнения основан на его дискретном представлении в виде. Неявный метод интегрирования Эйлера основан на ином дискретном представлении исходного уравнения:. Названия методов связаны с тем, что в первом случае неизвестная определяется дискретным уравнением в явном виде, во втором случае – в неявном виде. Неявный метод Эйлера по сравнению с явным методом обладает более высокой помехоустойчивостью, поэтому используется для интегрирования дифференциальных уравнений с разнотемповыми процессами на фоне помех.
| <== предыдущая | | | следующая ==> |
| написания студентом выпускной квалификационной работы | | | Методы оценки яйценоскости |
Date: 2016-07-22; view: 522; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |