Порядка при постановке многофакторных экспериментов

Обобщение изложенной выше методики на многофакторный эксперимент не связано с какими-либо принципиальными отличиями, кроме усложнения вычислений, требующих привлечения математического аппарата матричной алгебры для решения более громоздких систем линейных уравнений. Так, например, при двухфакторном эксперименте отличие линейной математической модели от использованного нами простейшего уравнения регрессии (5.1) будет заключаться в появлении дополнительного слагаемого, связанного с появлением второго значащего фактора − х₂. Уравнение линейной регрессии при этом будет иметь вид:

(11)

В результате подстановки в условие (3) расчетного значения , определяемого выражением (11), и последующего выполнения действий, аналогичных описанным выше, можно получить следующую систему уравнений, являющихся линейными относительно трех неизвестных коэффициентов регрессии k ₁, k ₂, b:

Сравнивая между собой системы уравнений для однофакторной модели и двухфакторной модели, можно констатировать, что число уравнений в этих системах, как и число слагаемых в правой части самих уравнений, равно числу неизвестных коэффициентов в линейных математических моделях. При этом с ростом числа факторов значительно усложняются алгебраические формулы для расчета коэффициентов. В частности, уже при двухфакторном эксперименте эти формулы имеют следующий вид:

где А, B, С, D, E, F – дополнительные промежуточные комплексы, определяемые по выражениям:

Из вышеизложенного следует, что в многофакторном эксперименте для расчета коэффициентов регрессии алгебраическим методом, даже при использовании наиболее простой двухфакторной линейной математической модели, кроме вычисления восьми сумм, присутствующих в уравнениях системы, требуется предварительное вычисление еще шести дополнительных промежуточных комплексов по формулам.

Общее количество предварительно вычисляемых параметров при этом становится равным 14, что на 10 параметров больше, чем требуется для обработки результатов однофакторного эксперимента.

Кроме того, при избыточном числе уровней в многофакторных экспериментах может резко возрастать общее число опытов. Так, например, если в двухфакторном эксперименте сохранить cемь уровней варьирования, использованных нами для расчета коэффициентов регрессии однофакторной линейной зависимости в предыдущем примере, то число опытов, требуемое для реализации ПФЭ-7² составит:

где р − число уровней, равное 7; q − число факторов, равное 2.

Однако производить такое большое число опытов для получения простых линейных зависимостей нецелесообразно. Известно, что любая прямая всегда может быть построена по двум точкам. Поэтому в тех случаях, когда линейный характер функции отклика не вызывает

сомнений, число уровней варьирования каждого фактора может быть сведено к минимальному значению р = 2 без какого-либо ущерба для точности математической модели. Таким образом, для реализации ПФЭ в данном случае достаточно поставить всего 4 опыта:

При этом необходимо сразу задать область определения функции отклика, в которой будет производиться эксперимент, ограничив интересующую часть факторной плоскости (или факторного пространства, при q > 2) предельными значениями каждого аргумента:

Согласно методике многофакторного эксперимента, поочередная установка факторов на нижний и верхний уровни дает возможность получения четырех характерных комбинаций, схематично показанных точками факторной плоскости на рис. 3.

Рис. 3. Геометрическая интерпретация факторной плоскости ПФЭ-2²

Координаты этих точек задают условия проведения серии опытов, необходимых для реализации плана двухуровневого полнофакторного эксперимента: ПФЭ−2². Номера точек соответствуют номерам опытов, а символы минус и плюс показывают, на каком из уровней (нижнем «−» или верхнем «+») должны быть установлены соответствующие факторы х 1 и х 2 в каждом из опытов.

Совокупность всех точек плана, отличающихся уровнями хотя бы одного фактора, называется спектром плана. Таким образом, схема, представленная на рис. 3, представляет собой не что иное, как геометрическую интерпретацию спектра плана ПФЭ-2².

Точка «0», являющаяся центром области эксперимента, называется центральной точкой плана. Координаты этой точки соответствует нулям нормализованной шкалы, по которой должен производиться отсчет всех факторов при переходе к безразмерному виду записи плана эксперимента.

Планы проведения любых многофакторных экспериментов удобно представлять в форме специальных таблиц, которые называются матрицами планов. Согласно определению, матрица плана представляет собой стандартную форму записи условий проведения эксперимента в виде

прямоугольной таблицы, строки которой отвечают опытам, а столбцы – факторам.

Примером такой матрицы может служить табл. 3.

Таблица 3

Пример матрицы плана полнофакторного

эксперимента ПФЭ−2²

Четыре первые строки табл. 3 представляют собой так называемое ядро плана. Пятая строка (нулевая точка) предназначена для сравнения фактических и прогнозных значений отклика в центре плана. Эта строка вводится для контроля и, как правило, не используется при расчете коэффициентов. Однако после нахождения коэффициентов в эту строку заносится рассчитанное при помощи полученной математической модели прогнозное значение отклика , которое сравнивается со средним экспериментальным значением . В том случае, если полученная разность значений не выходит за пределы требуемой точности, делается предварительный вывод о пригодности линейной модели для математического описания результатов данного эксперимента.

Нормализация факторов при ортогональном планировании. В матрицу планирования могут заноситься как натуральные, так и нормализованные значения факторов. Под нормализацией понимается преобразование натуральных значений факторов в безразмерные.

Процедура нормализации факторов производится для упрощения записи матрицы планирования и последующего облегчения обработки экспериментальных данных. По сути, эта процедура заключается в переносе точки отсчета уровней всех факторов в центр плана с одновременным переходом на такие единицы измерения каждого фактора, которые обеспечивают единичные числовые значения уровней на границах области эксперимента (х_{u , min} = −1 и х_u,max = +1).

Формально процедура нормализации сводится к тому, что, располагая минимальным и максимальным натуральными значениями (хu, min и хu,max), определяют некое среднее значение хu, 0 (в натуральном исчислении), которое для каждого u −го фактора принимается за ноль отсчета и, согласно, считается его основным уровнем, определяющим одну из координат центральной точки плана:

Далее определяются отсчитываемые от основного уровня интервалы варьирования Δ хu, которые в дальнейшем будут выполнять роль новых единиц измерения уровней каждого нормализованного фактора:

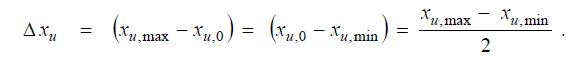
С учетом вышеизложенного формулы для прямого и обратного пересчета натурального значения любого u -го фактора в нормализованное и обратно имеют вид:

где * X_u и х_u – соответственно нормализованное и натуральное значения u –го фактора;

Δ x_u – интервал варьирования u –го фактора.

Согласно теории планируемого эксперимента зависимости откликов от нормализованных значений всех факторов описываются нормализованными уравнениями регрессии. Такие уравнения по своей структуре в точности соответствуют математическим моделям, использующим натуральные значения факторов. Все отличия между ними заключаются только в разных числовых значениях соответствующих коэффициентов. Так, например, для линейной математической модели (11) нормализованное уравнение регрессии может быть записано в виде

где B *; K*1; K*2 - коэффициенты нормализованного уравнения.

Зависимости между коэффициентами натуральных и нормализованных уравнений регрессии могут быть легко найдены с использованием двух следующих условий: равенства частных приращений отклика в пределах интервалов варьирования каждого u – го фактора и равенства значений отклика в центре плана, то есть

где Δ Xu* − интервал варьирования u –го нормализованного фактора, равный 1;

Xu,0* − нормализованная координата центра, равная 0;

U − общее количество слагаемых в уравнении регрессии.

Зависимости для пересчета соответствующих коэффициентов регрессии, полученные в результате решения уравнений, имеют следующий вид:

Нормализация факторов позволяет строить ортогональные матрицы планирования использование которых превращает расчет коэффициентов в простую арифметическую процедуру, независимо от числа слагаемых и сложности математических моделей.