Метод наименьших квадратов

Из математической статистики известны несколько научно обоснованных методов обработки результатов эксперимента. Однако наиболее востребованным и широко используемым по праву считается разработанный Лежандром и Гауссом на рубеже ХVIII – ХIХ веков метод

наименьших квадратов (МНК), составляющий основу регрессионного анализа.

Рассмотрим суть этого метода на примере аппроксимирования результатов однофакторного эксперимента линейным уравнением регрессии, которое представляется полиномом первой степени, имеющим в рассматриваемом случае наиболее простой вид

у = kx + b, (1)

где х – варьируемый фактор, уровни которого изменяются в процессе эксперимента, принимая ряд заданных дискретных значений;

y – отклик, значения которого фиксируются экспериментатором при каждом дискретном значении х;

k, b – неизвестные постоянные коэффициенты уравнения регрессии, используемого в качестве математической модели изучаемого процесса.

Покажем, как по результатам эксперимента, содержащим случайные погрешности, можно определять значения коэффициентов уравнения регрессии с наибольшей точностью.

Пусть в процессе эксперимента при каждом дискретном уровне х_i

(i = 1, 2,… N) было произведено n параллельных измерений отклика у_j

(j = 1, 2,… n). Дублирование измерений производилось равномерно на всех уровнях, так что число параллельных опытов в данном случае является постоянным (n = const) в пределах всего эксперимента. Средние арифметические значения отклика y_i при каждом дискретном

уровне фактора х_i определены по выражению

(2)

Эти среднеарифметические значения и выделенные вокруг них зоны естественного разброса результатов измерения схематично покажем на графике рис. 5.1.

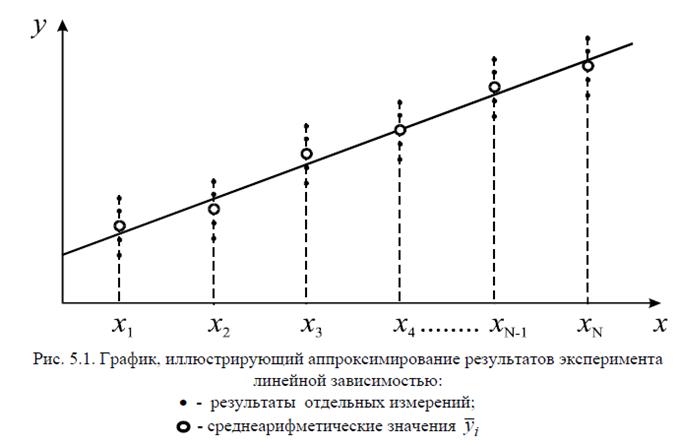
Анализируя этот график, видим, что точки, построенные на основании среднеарифметических значений, из-за естественного разброса никак не могут точно выстраиваться в одну линию. При этом возникает вопрос о том, как по результатам данного эксперимента можно построить прямую, которая проходила бы как можно ближе к истинной функциональной зависимости у = f(x).

В теории вероятностей доказывается, что наилучшим приближением к истинной функциональной зависимости всегда может служить такая кривая или прямая линия, сумма квадратов отклонений которой от экспериментальных точек по оси ординат минимальна. Этот принцип является основой метода наименьших квадратов.

Используя этот принцип, можно получить математическую запись основного условия МНК в следующем виде:

, (3)

где SUM – сумма квадратов отклонений;

– среднеарифметические экспериментальные значения отклика,

полученные при каждом i –м уровне фактора;

– расчетные значения отклика, определяемые при помощи выбранной математической модели.

Согласно условиям поставленной задачи, математической моделью в данном случае является линейная функция (1). Подставив значение , определяемое функциональной зависимостью (5.1), в (5.3), перепишем последнее в следующем виде:

. (4)

Так как значения и х_i всегда известны в результате выполненного эксперимента, полученное выражение следует рассматривать как целевую функцию двух неизвестных коэффициентов, являющихся аргументами этой функции: SUM = f(k; b). Анализ выражения (4) на экстремум позволяет получить систему уравнений для нахождения коэффициентов k и b линейной математической модели в наиболее простом частном случае: при однофакторном эксперименте.

Известно, что минимум функции нескольких переменных определяется координатами точки, в которой первые частные производные этой функции по каждому из аргументов равны нулю, а вторые – имеют положительное значение. Поэтому условие минимизации суммы квадратов отклонений в данном случае можно записать как:

С учетом этого условия после дифференцирования функции (4)получаем следующую систему уравнений:

Эта система в результате математических преобразований легко приводится к виду:

После решения системы уравнений с двумя неизвестными получаем следующие формулы для определения экспериментальных коэффициентов однофакторной линейной зависимости методом наименьших квадратов:

Полученные формулы позволяют по результатам однофакторного эксперимента определять параметры, обеспечивающие наилучшее приближение линейных математических моделей к действительным функциональным зависимостям между величинами.

Для практического использования этих формул необходимо по результатам эксперимента предварительно вычислить суммы четырех входящих в них комплексов.

Пример. Определим значения коэффициентов линейной регрессии по результатам однофакторного эксперимента, представленным в табл. 1.

Таблица 1

Исходные данные для расчета коэффициентов регрессии однофакторной линейной математической модели

Используя суммы, полученные в соответствующих столбцах табл. 1, по ранее выведенным формулам рассчитаем численные значения коэффициентов регрессии:

Таким образом, исследованная однофакторная функциональная зависимость может быть описана линейным уравнением, которое с учетом полученных коэффициентов будет иметь вид:

(10)

Для более строгого подтверждения адекватности принятой математической модели необходим регрессионный анализ, основанный на статистических методах проверки гипотез.