
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение оптимизационных задач
Многочисленные проблемы, связанные с распределением и использованием финансовых, трудовых и других ресурсов, планированием, управлением и оценкой эффективности производства, управлением запасами, календарным планированием работ, могут быть формализованы и решены с использованием специальных математических методов, объединенных общим названием - математическое программирование.
Наиболее общая математическая постановка задачи математического программирования - определить значения переменных Х 1, Х 2... Х n;, доставляющих максимум (минимум) заданной функции
 (1)
(1)
при условиях

Функцию W принято называть целевой функцией или показателем эффективности исследуемой экономической операции.
Приведем пример вербальной постановки задачи математического программирования.
Задача. Фабрика выпускает три вида изделий. Суточные ресурсы фабрики следующие: 700 единиц производственного оборудования; 800 единиц сырья; 600 единиц энергоресурсов. Расходы каждого вида ресурсов на единицу изделий каждого типа представлены в табл. 4
Таблица 4
Исходные данные задачи оптимизации
| Ресурсы | Виды изделий | ||
| А | В | С | |
| Оборудование | |||
| Сырьё | |||
| Э/ ресурсы |
Цена единицы изделия первого вида равна 8 ден. ед., изделия второго вида - 7 ден. ед., изделия третьего вида - 6 ден. ед.
Сколько ткани каждого вида необходимо производить в сутки, чтобы выручка от реализации готовой продукции была наибольшей?
Допущение: вся произведенная ткань реализуется. В данной задаче показателем эффективности W является выручка; переменными Х 1, Х 2, Х 3 - физические объемы производимой ткани первого, второго и третьего вида соответственно; ограничения fj (j = 1, 2, 3) связаны с располагаемыми ресурсами.
Общая характеристика задачи линейного программирования
Задача линейного программирования (ЛП) в общей постановке состоит в отыскании значений п переменных Х 1, Х 2, Х 3,...,, доставляющих экстремум функции:

при условиях
 (2)
(2)
Как следует из приведенных выражений, условия (2) представляют собой систему нестрогих линейных неравенств, а показатель эффективности W является аддитивной линейной функцией п переменных.
Вернувшись к задаче, нетрудно убедиться в том, что ее формально-математическая постановка соответствует общей постановке задачи линейного программирования.
Действительно, требуется определить значения переменных Х 1, Х 2, Х 3, доставляющие максимум целевой функции
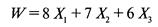
при ограничениях
 (3)
(3)
Ограничения-неравенства в задачах линейного программирования замещают равенствами, введя дополнительные переменные. Так, в случае (3) получим
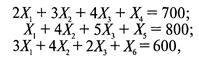 (4)
(4)
где Х 4, Х 5, Х 6 - дополнительные переменные.
С учетом последнего положения общая постановка задачи линейного программирования может быть записана в виде:
найти значения n переменных Х 1, Х 2, Х 3,..., Х п, доставляющие экстремум функции

при условиях
 (5)
(5)
Кроме того, дополнительно вводится условие неотрицательности всех переменных

Последнее условие требует, чтобы решение задачи было допустимым, т.е. неотрицательным.
Заметим, что в ряде случаев система ограничений может отличаться от (2) и (5). Однако следует помнить о том, что приведенная постановка задачи линейного программирования является общей, а значит, остальные случаи могут быть сведены к ней.
Допустимое решение (Х 1, Х 2,..., Х п), при котором функция (показатель) W принимает оптимальное (наилучшее) значение, называют оптимальным.
Частное решение системы уравнений (5), получаемое приравниванием нулю п из (п + т) переменных, называют базисным. При этом переменные, приравненные нулю, принято называть неосновными, или свободными. Оставшиеся переменные называют основными.
Оптимальное решение задачи ЛП ищут среди допустимых базисных решений. Для этого используют специфические свойства задачи ЛП, которые вводят рядом теорем. Из этих теорем непосредственно следует справедливость следующего положения:
Экстремум целевой функции является абсолютным и достигается хотя бы в одной крайней точке многогранника, задающего область определения задачи линейного программирования; данная точка соответствует допустимому базисному решению системы - уравнений ограничений.
Для решения задач линейного программирования в зависимости от их специфики применяют различные методы:
геометрический метод; симплекс-метод; распределительный метод и др.
Геометрический подход к решению задач линейного программирования
Геометрический метод решения задач ЛП имеет весьма ограниченное применение и главным образом используется для наглядной иллюстрации существа подобных задач.
В этой связи отметим, что если система ограничений задачи ЛИ задана в виде системы линейных неравенств с двумя переменными или в виде системы линейных уравнений, В которой число переменных на две больше, чем число уравнений, то такая задача может быть решена геометрически.
Если размерность задачи линейного программирования позволяет представить область определения переменных в виде многоугольника, расположенного в первом квадранте системы координат, то экстремум целевой функции находится в одной из его вершин, а ее координаты соответствуют оптимальному решению.
Пример выполнения задания
Содержательная постановка задачи
Фирма выпускает два вида тканей. Суточные ресурсы фирмы следующие: 700 единиц производственного оборудования; 800 единиц сырья; 600 единиц энергоресурсов. Расходы каждого вида ресурсов на единицу ткани каждого типа представлены в табл. 4.
Цена единицы ткани первого вида равна 8 ден. ед., а второго вида - 6 ден. ед.
Сколько единиц ткани каждого вида необходимо произвести в сутки, чтобы выручка от реализации готовой продукции была максимальной?
Математическая постановка задачи
Найти Х 1, Х 2, доставляющие максимум целевой функции

при ограничениях
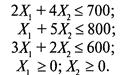
Геометрическое решение задачи
В системе координат (X 1, 0, Х 2) строим график линейной зависимости, полученной переходом от первого неравенства к равенству (рис. 1):

По аналогии получаем выражения для двух других линейных зависимостей

Изображаем графики данных зависимостей в той же системе координат и штриховкой выделяем область определения рассматриваемой задачи.
Затем на том же рисунке (рис. 5) изображаем прямую, полученную с использованием целевой функции для случая

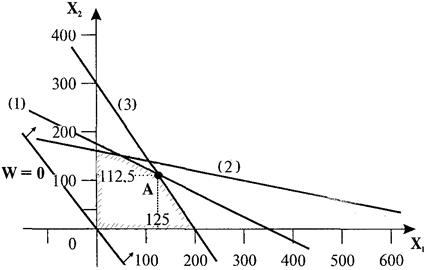
Рис. 5. Графическая интерпретация решения
оптимизационной задачи

График данной линейной зависимости перемещаем параллельно самому себе до вершины с максимальным значением целевой функции (при поиске минимума - линию, соответствующую функции цели перемещаем в противоположном направлении).
Координаты данной вершины (точка А) и соответствуют оптимальному решению задачи.
В этой точке пересекаются линии (1) и (3). Решая совместно систему из двух уравнений, соответствующих этим линиям, получаем координаты точки А:

Вычтем из первого уравнения второе и получим:
0 = 125 – Х 1
отсюда
Х 1 = 125.
Подставляя найденное значение в одно из уравнений, получим
Х 2 = 175 – ½ 125
отсюда
Х 2 = 112,5.
Подставляя значения переменных в целевую функцию, получим
W = 8·125 + 6·112,5 = 1675.
Выводы: продукции первого вида должно быть произведено 125 единиц, второго вида – 112,5. Максимальная выручка от реализации продукции составит 1675 ден.ед.
Варианты заданий
Исходные данные для своего варианта задания каждый студент формирует самостоятельно по следующему алгоритму:
1) обращение к таблице, содержащей выборку из таблицы случайных чисел, и извлечение из нее трёх чисел подряд (а 1, а 2, а 3), начиная с числа, соответствующего в таблице номеру варианта.
Таблица 5
Таблица случайных чисел
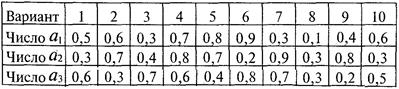
2) замена в задаче переменных в 1, в 2, в 3 числами, полученными по зависимостям

Примечание. ] с [ - означает целую часть от с.
Задача. Фирма выпускает два вида продукции А и В. Суточные ресурсы фирмы следующие:
в 1 - единиц производственного оборудования;
в 2 - единиц сырья;
в 3 - единиц электроэнергии.
Расходы каждого вида ресурсов на единицу продукции каждого типа представлены в табл. 6:
Таблица 6
| Ресурсы | Тип продукции | |
| А | В | |
| Оборудование | ||
| Сырьё | ||
| Э/ ресурсы |
Цена единицы продукции первого вида равна 8 ден. ед., а второго вида - 6 ден. ед.
Сколько единиц продукции каждого вида необходимо произвести в сутки, чтобы выручка от реализации готовой продукции была максимальной?
Date: 2016-07-18; view: 316; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |