Основы векторного исчисления

Вектор. Нулевой вектор. Длина (модуль) вектора.

Коллинеарные векторы. Компланарные векторы.

Равенство векторов. Сложение и вычитание векторов.

Законы сложения. Законы умножения вектора на число.

Скалярное произведение векторов и его свойства.

Единичные ортогональные векторы.

Векторное произведение векторов и его свойства.

Необходимое и достаточное условие коллинеарности векторов.

Необходимое и достаточное условие компланарности векторов.

Вектор – это направленный отрезок, соединяющий две точки в пространстве или в плоскости. Векторы обычно обозначаются либо маленькими буквами, либо начальной и конечной точками. Сверху обычно ставят чёрточку. Например, вектор, направленный из точки A к точке B, можно обозначить a, __ Нулевой вектор 0или 0 -это вектор, у которого начальная и конечная точки совпадают, т.e. A = B. Отсюда, 0 = – 0. Длина (модуль) вектора a - это длина отображающего его отрезка AB, обозначается | a |. В частности, | 0 | = 0. Векторы называются коллинеарными, если их направленные отрезки лежат на параллельных прямых. Коллинеарные векторы a и b обозначаются a || b. Три и более векторов называются компланарными, если они лежат в однойплоскости. Сложение векторов. Так как векторы - это направленные отрезки, то их сложение может быть выполнено геометрически. (Алгебраическое сложение векторов изложено ниже, в пункте «Единичные ортогональные векторы»). Предположим, что __ __ a = AB and b = CD, тогда вектор __ __ a + b = AB + CD есть результат выполнения двух операций: a) параллельного переноса одногоиз векторов таким образом, чтобы его начальная точка совпала с конечной точкой второго вектора; б) геометрического сложения, т.е.построения результирующего вектора, идущего от начальной точки неподвижного вектора к конечной точке перенесённого вектора.   Вычитание векторов. Эта операция сводится к предыдущей путём замены вычитаемого вектора на противоположный: a –b = a + (–b).   Законы сложения. I. a + b = b + a (П е р е м е с т и т е л ь н ы й закон). II. (a + b) + c = a + (b + c) (С о ч е т а т е л ь н ы й закон). III.a + 0= a. IV.a + (–a) = 0 .   Законы умножения вектора на число. I. 1 · a = a,0 · a = 0, m · 0 = 0, (– 1) · a = – a. II. m a = a m, | m a | = | m | · | a |. III. m (n a) = (m n) a. (С о ч е т а т е л ь н ы й закон умножения на число). IV. (m + n) a = m a + n a, (Р а с п р е д е л и т е л ь н ы й m (a + b)= m a + m b. закон умножения на число).   Скалярное произведение векторов. __ __ Угол между ненулевыми векторами AB и CD – это угол, образованный векторами при их параллельном переносе до совмещения точек A и C. Скалярным произведением векторов a и b называется число, равное произведению их длин на косинус угла между ними: 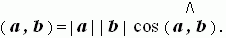  Если один из векторов нулевой, то их скалярное произведение в соответствии с определением равно нулю: (a, 0) = (0 ,b) = 0. Если оба вектора ненулевые, то косинус угла между ними вычисляется по формуле: 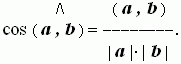  Скалярное произведение (a, a), равное | a | 2, называется скалярным квадратом. Длина вектора a и его скалярный квадрат связаны соотношением: 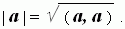  Скалярное произведение двух векторов: - положительно, если угол между векторами острый; - отрицательно, если угол между векторами тупой. Скалярное произведение двух ненулевых векторов равно нулю тогда итолько тогда, когда угол между ними прямой, т.е. когда эти векторы перпендикулярны (ортогональны):     Свойства скалярного произведения. Для любых векторов a,b, c и любого числа m справедливы следующие соотношения: I. (a,b) = (b, a). (П е р е м е с т и т е л ь н ы й закон) II. (m a,b) = m (a,b). III. (a + b, c) = (a,c) + (b,c). (Р а с п р е д е л и т е л ь н ы й закон)   Единичные ортогональные векторы. В любой прямоугольной системе координат можно ввести единичные попарно ортогональные векторы i, j и k, связанные с координатными осями: i – с осью Х, j – с осью Y и k – с осью Z. В соответствии с этим определением:   (i, j) = (i, k) = (j, k) = 0,   | i | = | j | = | k | = 1.   Любой вектор a может быть выражен через эти векторы единственным образом: a = x i + y j + z k. Другая форма записи: a = (x, y, z). Здесь x, y, z - координаты вектора a в этой системе координат. В соответствии с последним соотношением и свойствами единичных ортогональных векторов i, j, k скалярное произведение двух векторов можно выразить иначе. Пусть a = (x, y, z); b = (u, v, w). Тогда (a,b) = xu + yv + zw. Скалярное произведение двух векторов равно сумме произведений соответствующих координат. Длина (модуль) вектора a = (x, y, z) равна:   Кроме того, теперь мы получаем возможность проведения алгебраических операций над векторами, а именно, сложение и вычитание векторов можетвыполняться по координатам: a +b = (x + u, y + v, z + w); a – b = (x – u, y – v, z – w). Векторное произведение векторов. Векторным произведением [ a,b ] векторов a и b (в указанном порядке) называется вектор: 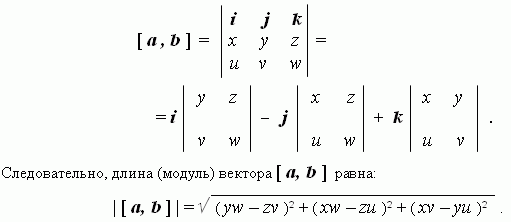Существует другая формула длины вектора [ a, b ]:   /\ | [ a, b ] | = | a | | b | sin (a, b),   т.e. длина (модуль) векторного произведения векторов a и b равнапроизведению длин (модулей) этих векторов на синус угла между ними. Иначе говоря: длина (модуль) вектора [ a, b ] численно равна площади параллелограмма, построенного на векторах a и b. Свойства векторного произведения. I. Вектор [ a, b ] перпендикулярен (ортогонален) обоим векторам a и b. (Докажите это, пожалуйста!). II. [ a,b ] = – [ b, a ]. III. [ m a,b ] = m [ a,b ]. IV. [ a + b, c ] = [ a,c ] + [ b,c ]. V. [ a, [ b, c ] ] = b (a, c) – c (a, b). VI. [ [ a,b ], c ] = b (a, c) – a (b, c).   Необходимое и достаточное условие коллинеарности векторов a = (x,y, z) и b = (u, v, w): 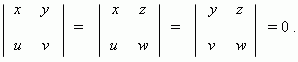Необходимое и достаточное условие компланарности векторов a = (x, y, z), b = (u, v, w) и c = (p, q, r): 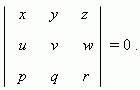П р и м е р. Даны векторы: a = (1, 2, 3) и b = (– 2, 0,4). Вычислить их скалярное и векторное произведения и угол между этими векторами.   Р е ш е н и е. Используя соответствующие формулы (см. выше), получим: a). скалярное произведение:   (a, b) = 1 · (– 2) + 2 · 0 + 3 · 4 = 10; б). векторное произведение:

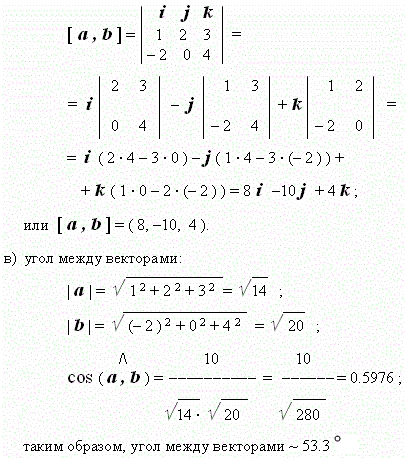
Комплексные числа

Мнимые и комплексные числа. Абсцисса и ордината

комплексного числа. Сопряжённые комплексные числа.

Операции с комплексными числами. Геометрическое

представление комплексных чисел. Комплексная плоскость.