
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Положительной связи, однако не позволяет ввести обобщенную ее меру
Примеры различного вида диаграмм, позволяющих графически интерпретировать характер связи между наборами данных А'и Y, приведены на рис. 5.16.
Прямая связь
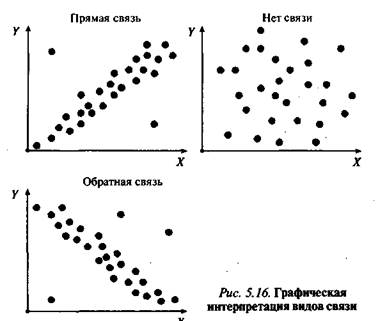
Ковариация. Без сомнения, необходимо поставить вопрос о введении определенной меры для выражения степени соответствия между наборами данных Х и Y. Точнее сказать, той меры, которая позволит выявить степень соответствия больших значений из множества X большим же значением из множества Y (прямая связь) либо, наоборот, больших значений из Х малым из Y (обратная связь). Подобная мера связи называется ковариацией. Для выявления смысла понятия «ковариация» удобно рассмотреть результаты выполнения группой испытуемых двух тестов Х и Y, образующих два множества.
Пусть результаты по первому тесту X— это множество Xi (i = 1, 2,..., N), а по второму тесту — Yi(i= 1,2,..., /V). Тогда для установления меры связи между результатами тестирования необходимо сравнить положение каждого тестируемого в выборках относительно данных по тесту Х и по тесту Y. Обычно это положение устанавливают по отношению к среднему, тогда степень соответствия результатов i-го испытуемого в первом (А) и во втором (Y) тестированиях будет проявляться в величине и знаке произведения отклонений
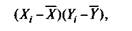
где Xi Yi — результаты /-го испытуемого в первом и во втором тестированиях соответственно (/= 1, 2,..., N); X, Y — средние значения результатов по тестам; N — число учеников тестируемой группы.
При подсчете произведений для различных результатов учеников тестируемой группы выявляется интересная закономерность. Если результат i-го ученика выше среднего балла по обоим тестам,
то произведение (Xj-X)(Yj-Y) будет большим и положительным.
Аналогично выглядит произведение отклонений для случая, когда результаты ученика намного ниже средних баллов по обоим тестам, поскольку произведение двух отрицательных чисел
(Xj г - X < О и I - Y < 0) также больше нуля.
Таким образом, при прямой связи значений Х( и Yi(i=l, 2,..., N) по тестам Х и К большие значения X. соотносятся с большими значениями Y.f, а малые значения X. с малыми Yr Тогда произведение (Xj - X)(Yj - Y) будет положительным для всех или почти всех
результатов учеников тестируемой группы. Соответственно большой и положительной получится сумма всех произведений, т.е.

будет намного больше нуля для случая, когда результаты по тестам Х и У связаны прямой зависимостью.
При обратной связи результатов тестирования значения Xf выше
(ниже) среднего X по тесту X сменяются на значения Yt ниже (выше) среднего F по тесту Y, а сумма
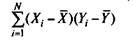
будет велика по модулю и меньше нуля в силу отрицательного знака всех или почти всех произведений (Xj - X)(Yi - F).
Наконец, в том случае, когда систематической связи между результатами учеников по тестам Хн Уне наблюдается, знак произведения (X,-X)(Yj-Y) будет хаотически меняться. Скорее всего, в сумме произведений, подсчитанных по достаточно большой выборке учеников, положительные слагаемые будут уравновешиваться отрицательными и потому сумма произведений
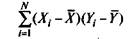
получится близкой к нулю.
Таким образом, произведение (Xj-X)(Yj-Y) по знаку и абсолютной величине отражает характер связи между наборами данных, что является ее несомненным достоинством. Однако выбору этой суммы в качестве обобщенной меры связи препятствует ее зависимость от объема выборки объектов, участвующих в измерении, в то время как для сравнения мер связи между результатами тестовых измерений по выборкам разного объема необходимо иметь показатель, не зависящий от размеров выборок. Такой показатель позволяет получить операция усреднения, осуществляемая путем деления суммы произведений отклонений на число испытуемых в выборке. Поэтому в качестве меры связи выбирается величина
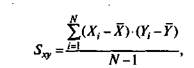
которая называется ковариацией и обозначается символом 5.
Коэффициент корреляции Пирсона. Для повышения сопоставимости оценок показателей связи по выборкам с различной дисперсией ковариацию делят на стандартные отклонения. Таким образом, S^ необходимо разделить на Sx и Sy, где Sx и S' — стандартные отклонения по множествам Х и У соответственно. В результате получается величина, которая называется коэффициентом корреляции Пирсона 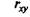 :
:
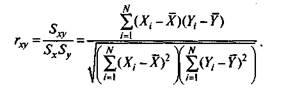
Переход к другой, не содержащей X и Y формуле показан в приложении 5.4.
Коэффициент (р. Для оценки связи между результатами выполнения двух заданий теста коэффициент корреляции Пирсона
необходимо преобразовать, поскольку результаты выполнения заданий представляются в дихотомической шкале (см. табл. 5.3). Действительно, в матрице содержатся столбцы из нулей и единиц. Каждая единица и каждый нуль соответствуют результатам ответов учеников на задания теста.
Преобразованный коэффициент Пирсона, вычисляемый по дихотомическим данным, называется коэффициентом «фи». (Переход от г к ф-коэффиценту показан в приложении 5.5.) После перехода формула для вычисления коэффициента корреляции фij результатов по двум заданиям теста с номерами i и j имеет вид

Результаты подсчета значений коэффициента корреляции между результатами по отдельным заданиям теста сводятся в матрицу, которая для данных табл. 5.3 имеет вид табл. 5.10.
Интерпретация. Анализ значений коэффициента корреляции в табл. 5.10 позволяет выделить задания 3 и 8 теста. Поданным таблицы, задание 3 отрицательно коррелирует с заданиями 7, 8,9 и 10 теста. О том, что «виновато» третье, а не другие задания теста, свидетельствует анализ значений коэффициента корреляции в столбцах с номерами семь, девять и десять. В них просматривается только один минус на месте, соответствующем заданию теста 3, которое в свою очередь отрицательно коррелирует с четырьмя заданиями теста.
Таблица 5.10. Матрица коэффициентов корреляции заданий для табл. 5.3
| 1,0000 | 0,6667 | 0,5092 | 0,4082 | 0,3333 | 0,3333 | -0,4082 | 0,2182 | 0,1667 | 0,1111 | |
| 0,6667 | 1,0000 | 0,2182 | 0,6124 | 0,0000 | 0,0000 | -0,1021 | 0,3273 | 0,2500 | 0,1667 | |
| 0,5092 | 0,2182 | 1,0000 | 0,3563 | 0,2182 | 0,2182 | -0,3563 | -0,476 | -0,2182 | -0,5092 | |
| 0,4082 | 0,6124 | 0,3563 | 1,0000 | 0,4082 | 0,4082 | -0,1667 | 0,5345 | 0,4082 | 0,2722 | |
| 0,3333 | 0,0000 | 0,2182 | 0,4082 | 1,0000 | 0,6000 | 0,0000 | 0,6547 | 0,5000 | 0,3333 | |
| 0,3333 | 0,0000 | 0,2182 | 0,4082 | 0,6000 | 1,0000 | 0,0000 | 0,2182 | 0,5000 | 0,3333 | |
| -0,4082 | -0,1021 | -0,3563 | - 0,1667 | 0,0000 | 0,0000 | 1,0000 | 0,3563 | 0,6124 | 0,4082 | |
| 0,2182 | 0,3273 | -0,476 | 0,5345 | 0,6547 | 0,2182 | 0,3563 | 1,0000 | 0,7638 | 0,5092 | |
| 0,1667 | 0,2500 | -0,2182 | 0,4082 | 0,5000 | 0,5000 | 0,6124 | 0,7638 | 1,0000 | 0,6667 | |
| 0,1111 | 0,1667 | -0,5092 | 0,2722 | 0,3333 | 0,3333 | 0,4082 | 0,5092 | 0,6667 | 1,0000 | |
| Суммы | 3,3385 | 3,1392 | 1,3888 | 4,2417 | 4,0478 | 3,6114 | 1,3436 | 4,5346 | 4,6495 | 3,2915 |
Аналогичная ситуация наблюдается в столбце, соответствующем заданию 8 теста. Отрицательные значения коэффициента корреляции указывают на определенный просчет разработчиков в содержании заданий 3 и 8 теста. Наиболее распространенная причина — отсутствие предметной чистоты содержания — нередко встречается при разработке самых разных тестов.
Понятно, что предметная чистота — скорее идеализируемое, чем реальное требование к содержанию любого теста. Например, в тесте по физике всегда встречаются задания с большим количеством математических преобразований, в тесте по биологии — задания, требующие серьезных знаний по химии, в тесте по истории — задания, рассчитанные на выявление культурологических знаний, и т. п. Поэтому говорить об отсутствии пересечения содержания заданий одной учебной дисциплины с содержанием другой в чистом виде не приходится. Можно лишь стремиться к тому, чтобы при выполнении каждого задания доминировали знания по проверяемому предмету.
По-видимому, противоположная ситуация наблюдалась в заданиях 3 и 8, отрицательные значения корреляции по которым указывают на отсутствие связи их содержания с содержанием других заданий теста.
Таким образом, задания 3 и 8 для повышения гомогенности содержания необходимо удалить из теста. Конечно, окончательное решение остается за автором, поскольку оно бессмысленно без тщательного анализа содержания заданий теста. Правда, подобное решение об удалении заданий может быть принято в том случае, когда эмпирические результаты собраны по репрезентативной выборке учеников. Если представительность выборки не достигнута, то появление минусов может не отражать ни в коей мере реальную ситуацию с содержанием заданий теста.
Анализ 9-го столбца с максимальной суммой 4,6495, приведенной в конце, указывает на наличие ряда довольно высоких значений коэффициента корреляции (ср9 g = 0,6124; <р9 7 = 0,7638; <р9 10 = 0,6667), каждое из которых может получить различную трактовку в зависимости от вида разрабатываемого теста.
Для тематических тестов высокая корреляция между заданиями неизбежна, так как задания отражают слабо варьирующее, исходное содержание, что вполне оправдано назначением теста.
Однако для итоговых тестов высокой корреляции между заданиями по возможности стараются избегать тестов, оценивающих одинаковые содержательные элементы, поскольку вряд ли имеет смысл включать в итоговый тест несколько заданий. Поэтому в итоговых тестах обычно стремятся к невысокой положительной корреляции, когда значения коэффициента варьируют в интервале (0; 0,3) и каждое задание привносит свой специфический вклад в общее содержание теста.
Десятый шаг. На десятом шаге с помощью подсчета значений коэффициента бисериальной корреляции оценивается валидность отдельных заданий теста.
Коэффициент бисериальной корреляции используется в том случае, когда один набор значений распределения задается в дихотомической шкале, а другой — в интервальной (подробнее см. гл. 7). Тогда в качестве показателя связи между распределениями выбирают бисериальный коэффициент. Под эту ситуацию подпадает подсчет корреляции между результатами выполнения каждого задания (дихотомическая шкала) и суммой баллов испытуемых (интервальная или квазиинтервальная шкала) по заданиям теста.
Объяснение, на котором основан вывод формулы для подсчета бисериального коэффициента корреляции приводится в книге [9] и ряде других изданий. Формула для подсчета, полученная по результатам вывода, имеет вид
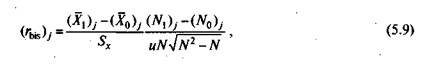
где (Х{)j — среднее значение индивидуальных баллов испытуемых,
выполнивших верно j-е задание теста; (X0)j — среднее значение
индивидуальных баллов испытуемых, выполнивших неверно j-е задание теста; Sx — стандартное отклонение по множеству значений индивидуальных баллов; (Л^).— число испытуемых, выполнивших верно j-е задание теста; (1ч0),— число испытуемых, выполнивших неверно j-е задание теста; N— общее число испытуемых, N= N{ + N0;u — ордината нормированного нормального распределения в точке, за которой лежит 100 (Ni/N) процентов площади под нормальной кривой.
Вычисление по формуле (5.9) требует использования специальных таблиц для нахождения ординат стандартной нормальной кривой и определенной математической подготовки. Поэтому нередко используют другой коэффициент корреляции, получивший название точечно-бисериального коэффициента — г pbis. Основания для подобной замены вполне понятны, поскольку и точечно-бисе-риальный и бисериальный коэффициенты очень похожи и вычисляются по сходным наборам данных. Однако формула для г bis намного проще, поэтому именно ему часто отдают предпочтение в практической работе. Помимо простоты в вычислении, точечно-бисериальный коэффициент по сравнению с бисериальным обладает еще одним важным преимуществом. Для подсчета значения лpbis не нужны те гипотезы, которые выдвигаются в силу необходимости относительно нормального характера распределения дихотомических данных при определении меры связи по формуле (5.9).
Предположение о нормальном распределении весьма существенно для вычисления rpbis. В том случае, когда гипотеза о нормальности нарушается, значения гмогут выходить за границы интервала [-1;+1], смещаясь в ту или иную сторону вдоль числовой прямой.
В отличие от бисериального точечно-бисериальный коэффициент не бывает больше +1 или меньше — 1. Формула для вычисления значения rpbis, имеет вид
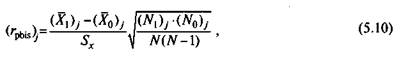
где все обозначения те же, что и в формуле (5.9).
Формула (5.10) может быть представлена в виде одного из двух вариантов, эквивалентных исходному выражению:
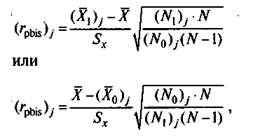
где все обозначения прежние и X — среднее значение всех индивидуальных баллов по выборке учеников.
С точки зрения интерпретации удобнее всего первая формула (5.10), которая используется ниже для данных матрицы в табл. 5.3. Например, для результатов по заданию 5
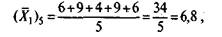
так как 1,4, 5, 9 и 10-й испытуемые выполнили задание 5 верно;
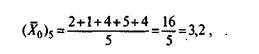
так как 2, 3, 6, 7 и 8-й испытуемые выполнили задание 5 неверно. Стандартное отклонение, подсчитанное для рассматриваемого примера ранее,

Более точные значения rbis, рассчитанные с помощью компьютерных программ для данных матрицы в табл. (5.3), приводятся в табл. 5.11.
Интерпретация. Анализ значений коэффициента бисериальной корреляции в табл. 5.11 указывает на два довольно неудачных задания теста. Это те же самые третье [(rtis)3 = 0,26] и восьмое rbis = 0,26 задания. Полученный вывод дает ценную информацию о низкой валидности заданий 3 и 8 теста. Эти задания следует признать неудачными и для улучшения теста их необходимо удалить.
В целом задание можно считать валидным, когда значение (rbis).= 0,5. Под этот критерий подпадают все, кроме двух заданий (третьего и восьмого) рассматриваемого примера матрицы теста.
Оценка валидности задания позволяет судить о том, насколько задание пригодно для работы в соответствии с общей целью создания теста. Если эта цель — дифференциация учеников по уровню подготовки, то валидные задания должны четко отделять хорошо подготовленных от слабо подготовленных учеников тестируемой группы.
Решающую роль в оценке валидности задания играет разность
(A7, )j -(X0)j, находящаяся в числителе дроби формулы (5.10). Чем
выше значение этой разности, тем лучше работает задание на общую цель дифференциации испытуемых, выполняющих тест. Значения, близкие к нулю, указывают на низкую дифференцирующую способность задания теста. В том случае, когда в разности доминирует вклад (Уо), а не (Х1), задание следует просто удалить из теста.
В нем побеждают слабые ученики, а сильные выбирают неверный ответ либо пропускают задание при выполнении теста. Таким образом, подлежат выбросу все задания, у которых rbis< 0.-
Таблица 5.11. Значение коэффициента бисериальной корреляции десяти заданий теста (табл. 5.3) с суммой
Баллов
| № | ||||||||||
| Задание | ||||||||||
| (rbis)y | 0,8032 | 0,7.887 | 0,7378 | 0,7229 | 0,6426 | . 0,5355 | 0,5355 | 0,5020 | 0,2629 | 0,2459 |
5.3. МЕТОДЫ ОБРАБОТКИ ДАННЫХ В РАМКАХ СОВРЕМЕННОЙ ТЕОРИИ СОЗДАНИЯ ТЕСТОВ
Под современной теорией понимается существующая на Западе Item Response Theory (IRT), предназначенная для оценки латентных параметров испытуемых и параметров заданий теста посредством применения математико-статистических моделей измерения [31,46,47„ 50 и др.]. IRT является частью более общей теории латентно-структурного анализа, хотя каждое из этих направлений имеет свои особенности. В частности, в теории латентно-структурного анализа оцениваемые значения параметров рассматриваются как некоторые дискретные точки на оси латентной переменной, в то время как в IRT распределения переменных предполагаются непрерывными.
В отличие от классической теории тестов, для IRT характерно стремление к фундаментальному теоретическому подходу и вместе с тем к корректному решению целого ряда практических задач педагогического измерения. В практическом плане это стремление неизбежно сопряжено с некоторыми трудностями, которые, кстати, не всегда осознаются ведущими тестологами — создателями современной теории тестов. В частности, необходимо привлечение довольно сложного математико-статистического аппарата, использование дорогостоящей компьютерной техники, нужна разработка специальных программных продуктов.
Эти трудности иногда кажутся непреодолимыми неопытным создателям, а тем более пользователям педагогических тестов, поэтому и первые и вторые иногда приходят к неверному выводу и полностью отказываются от IRT в пользу классической теории. Это решение, без сомнения, ошибочно. В конечном счете оно обязательно приводит к неполному извлечению информации из эмпирических результатов тестирования, к созданию неэффективных новых тестов или к неэффективным оценкам испытуемых при использовании общепринятых старых. Окончательное решение в пользу того или иного подхода лучше все же оставить до полного ознакомления со всеми преимуществами и возможностями, которые дает IRT.
Другой, более гибкий подход основан на взаимодействии этих теорий. Такое взаимодействие означает, что разработку теста следует разбить на два этапа. На первом этапе создания теста из набора предтестовых заданий эмпирические данные лучше обрабатывать с помощью более простого, но и менее эффективного математико-статистического аппарата классической теории тестов. На втором этапе, в процессе углубленного анализа качества заданий, для объективной оценки их параметров необходимо привлекать аппарат IRT.
К наиболее значимым преимуществам IRT обычно относят следующие.
• Устойчивость и объективность оценок параметра, характеризующего уровень подготовки испытуемых. Устойчивость можно считать наиболее важным преимуществом IRT. Источником ее является относительная инвариантность оценок параметра испытуемых от трудности заданий теста.
• Устойчивость и объективность оценок параметра трудности заданий, их независимость от свойств выборки испытуемых, выполняющих тест.
• Возможность измерения значений параметров испытуемых и заданий теста в одной и той же шкале, имеющей свойства интервальной. Последнее преимущество крайне важно, поскольку преобразование исходных величин разного происхождения в одну стандартную шкалу позволяет соотнести уровень знаний любого испытуемого с мерой трудности каждого задания теста. Практическое значение введения единой шкалы трудно переоценить. Особенную важность она приобретает в последние годы, поскольку на ней основана организация современного адаптивного автоматизированного контроля знаний, который на сегодняшний день является наиболее эффективной формой оценки знаний школьников или студентов.
С помощью IRT можно предсказать вероятность правильного выполнения заданий теста любым испытуемым в выборке до предъявления теста группе учеников, выявить эффективность различных по трудности заданий, используемых для оценки знаний, отличающихся по подготовке учеников тестируемой группы.
Вообще говоря, даже одного из перечисленных преимуществ было бы достаточно для того, чтобы отдать предпочтение IRT при создании теста. Однако эти преимущества не случайны. Они подкреплены соответствующим научным аппаратом, для которого характерно стремление к строгому формализованному представлению и анализу эмпирических данных. Соответственно, в IRT исходят из ряда строгих предположений как о характере оцениваемых параметров, так и о характере процессов, протекающих при выполнении заданий теста группой испытуемых.
Первоначально в IRT вводится основное предположение о существовании некоторой взаимосвязи между наблюдаемыми результатами тестирования и латентными (скрытыми от непосредственного наблюдения) качествами испытуемых, выполняющих тест. Обычно эти латентные качества трактуются как способности испытуемых или как уровни подготовки по предмету в зависимости от целей измерения, которые выдвигаются при создании педагогического теста.
Предполагается, что каждому испытуемому ставится в соответствие только одно значение латентного параметра, определяющего наблюдаемые результаты выполнения теста. Требование одномерности не носит, как правило, противоречивого характера, так как логика разработчика теста часто следует этому образцу. Он выдвигает гипотезу о том, что, скажем, создаваемый тест призван измерить уровень подготовки по предмету или по другому, меньшему объему содержания курса. Однако это требование существенно снижает возможности IRT в той ситуации, когда создается тест не по одной конкретной учебной дисциплине и не все задания в нем связаны с определенной областью знаний. В последнем случае на первом этапе формирования теста необходимо удалить задания, не удовлетворяющие требованию одномерности. Затем из удаленных заданий сформировать субтесты, отбирая задания по признаку одномерности оцениваемого латентного параметра испытуемых.
Разумеется, можно пойти и по другому пути и использовать тест с не удаленными заданиями. Тогда при обработке эмпирических результатов тестирования лучше обратиться к классической теории тестов. Правда, интерпретация полученных индивидуальных баллов требует соблюдения определенных мер предосторожности. Неопытный пользователь теста, плохо понимающий, каким путем был получен тот или иной индивидуальный балл, легко может прийти к его неверной интерпретации. Скорее всего, следует отдать предпочтение созданию гомогенных тестов, допускающих корректную обработку эмпирических результатов тестирования, а затем разрабатывать методы объединения отдельных оценок в одну общую, как это необходимо, например, при оценке достижений в обучении с помощью гетерогенных полидисциплинарных тестов.
Другие предположения носят специальный характер и связаны с математико-статистическим аппаратом, используемым в IRT для обработки эмпирических данных тестирования. Среди них можно выделить одно наиболее важное для понимания существенного различия между IRT и классической теорией тестов. Это предположение о характере измеряемых параметров испытуемых и заданий теста.
В отличие от классической теории, где индивидуальный балл тестируемого рассматривается как постоянное число, в IRT латентный параметр трактуется как некоторая переменная. Начальное значение параметра получается непосредственно из эмпирических данных тестирования. Переменный характер измеряемой величины указывает на возможность последовательного приближения к объективным оценкам параметра с помощью тех или иных итерационных методов.
Математические модели современной теории тестов. В рамках основного предположения IRT устанавливается связь между латентными параметрами испытуемых и наблюдаемыми результатами выполнения теста. При установлении связи важно понимать, что первопричиной являются латентные параметры. Если говорить точнее, то взаимодействие двух множеств значений латентных параметров порождает наблюдаемые результаты выполнения теста.
Элементы первого множества — это значения латентного параметра, определяющего уровень подготовки W испытуемых 0i, (i= 1, 2,..., N). Второе множество образуют значения латентного параметра рi., (i= 1, 2,..., n ), равные трудностям n заданий теста. Идея взаимодействия двух множеств отражена на рис. 5.17.

|
Однако на практике всегда ставится обратная задача: по ответам испытуемых на задания теста оценить значения латентных параметров Q и b. Для ее решения нужно ответить по меньшей мере на два вопроса. Первый связан с выбором вида соотношения между латентными параметрами Q и b. Идея установления соотношения принадлежит датскому математику Г. Ращу, который предложил ввести его в виде разности Q - b, предполагая, что параметры Q и b оцениваются в одной и той же шкале [52].
Значение параметра Q можно рассматривать как положение i-го испытуемого, а значение bj — как положение j-го задания на одной и той же оси переменных Q и b. В таком случае идея введения разности параметров получает интересную геометрическую интерпретацию. Абсолютная величина разности Qi-bi — это расстояние, на котором находится испытуемый с уровнем подготовки Q от задания с трудностью р. Если эта разность велика по модулю и отрицательна, то задание бесполезно для измерения уровня знаний i-го ученика. Ученик наверняка не может выполнить его верно. Большие положительные значения этой разности тоже не представляют интереса ни для процесса контроля, ни для обучения i-го испытуемого. Задание такой трудности давно им освоено, и он наверняка справится с ним успешно при выполнении теста. С точки зрения подхода, предлагаемого в IRT, такие задания неэффективны для оценивания данного значения 9.
Конечно, в том случае, когда Q незначительно больше ф, испытуемый может ошибиться в задании, хотя, скорее всего, выполнит его верно. При отрицательных значениях разности Q — b испытуемого, вероятнее всего, ждет неуспех, кроме исключительных ситуаций, когда возможно угадывание правильного ответа.
Ответ на второй вопрос, который является центральным в IRT, связан с выбором математической модели для описания рассматриваемой связи между латентными параметрами и наблюдаемыми результатами выполнения теста. Следуя основному предположению IRT, можно утверждать, что есть некоторая математическая модель взаимосвязи между эмпирическими результатами тестирования и значениями латентных переменных 0 и р.
При выборе модели следует учитывать, что в реальных условиях на наблюдаемые результаты оказывают влияние как случайные, так и неслучайные факторы. Несмотря на всю «случайность» отдельных результатов тестирования, проявляется относительная инвариантность значений латентных переменных от конкретного испытания или от ряда испытаний. Например, определенная устойчивость частот появлений значений переменных 0,, 02,..., 0^ наблюдается при многократном тестировании группы Л1'обучаемых параллельными тестами. Эта устойчивость является основанием для использования понятия вероятности события как меры возможности его появления. В качестве такого события обычно выбирается правильный ответ j-го испытуемого на j-е задание теста. Условную вероятность правильного выполнения обучаемыми заданий теста выражают с помощью различных математических моделей, которые записываются как функции одной переменной.
В частности, можно рассматривать условную вероятность правильного выполнения /-м испытуемым с уровнем подготовки Q различных по трудности заданий теста, считая 6, параметром i -го ученика, а b — независимой переменной. В этом случае условная вероятность будет функцией латентной переменной b:
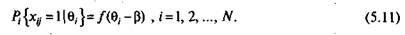
Аналогично вводится условная вероятность правильного выполнения у-го задания трудностью р. различными испытуемыми группы. Здесь независимой переменной является 0, а р.— параметр, определяющий трудность/- го задания теста:
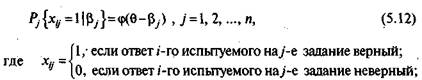
N— число испытуемых; п — количество заданий в тесте.
Если подставить в функцию ^.(0) значение переменной 0 = 0,. или в функцию /'ДР) значение р = Р(., то получится выражение для вероятности PtJ, значения которой можно охарактеризовать следующим образом:
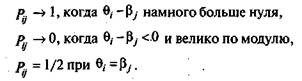
Связь между значениями разности Qi - bj и вероятностью правильного ответа i-го испытуемого на j-е задание теста показана на рис. 5.18.
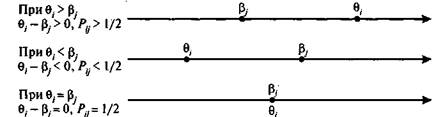
Рис. 5.18. Соотношение между значениями разности Qi ~ bj и вероятностью правильного ответа
В теории IRT функции f(b) и фи (Q) получили название Item Response Functions (IRF). Специальное название имеют и их графики. График функции Рi — это характеристическая кривая j-го задания (ICC), а график функции Рi— индивидуальная кривая i-го испытуемого (РСС).
При выборе вида функций Р. и Р. учитываются обстоятельства как эмпирического, так и математического характера. Подробный анализ оснований для такого выбора можно найти, например, в работе [50].
В предположении нормального распределения значений латентных переменных вир таких функций предлагаются две. Одна из них, обычно обозначаемая \|/(х), относится к семейству логистических кривых, другая Ф(х) является интегральной функцией нормированного нормального распределения. Поскольку для одних и тех же значений х ординаты точек графиков функций Ф(х) и \|/(1,7;с) отличаются друг от друга достаточно мало, то в том, что их две, нет ни ошибки, ни противоречия. А именно для всех х, принадлежащих области определения этих функций,

Наиболее сильный аргумент в пользу логистической функции связан не с качеством измерений, а с относительной простотой ее аналитического задания, выгодной при оценивании параметров 0 и р. Поэтому в практических приложениях предпочтение обычно отдают функции \|/(1,7х).
Число параметров, входящих в аналитическое задание функций, является основанием для подразделения семейства IRF на классы. Среди логистических функций различают:
• однопараметрическую модель Г. Раша

где Q и b — независимые переменные для первой и второй функций соответственно;
• двухпараметрическую модель А. Бирнбаума

Кроме прежних обозначений в формулах (5.16) и (5.17) появляются параметры аi и аj. Параметр а, был введен А. Бирнбаумом (A. Birnbaurm) [50] для характеристики дифференцирующей способности задания при измерении различных значений в; параметр at указывает на меру структурированности знаний ученика;
• трехпараметрическую модель А. Бирнбаума
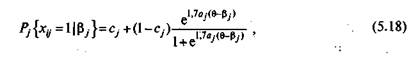
где с. является третьим параметром модели, характеризующим вероятность правильного ответа на задание j в том случае, если этот ответ угадан, а не основан на знаниях ученика.
В каждой из представленных моделей параметры Q и b выражаются как шкалированные показатели единой для всех моделей шкалы логитов. Введение единой шкалы для элементов двух различных множеств — значений 0 и значений b — позволяет решить ряд вопросов, как теоретических, так и практических. В частности, благодаря единой шкале можно ввести взаимосвязь между переменными в виде разности Q — b, корректно сравнить результаты учеников, полученные с помощью различных тестов, подобрать оптимальные значения b, позволяющие измерить искомое Q с минимальной ошибкой измерения. В целом эти важные преимущества позволяют преодолеть ряд существенных недостатков классической теории тестов и значительно повысить эффективность тестовых измерений.
Перевод значений Q и b в общую шкалу логитов с помощью специальных преобразований рассмотрен в следующем разделе для модели Г. Раша.
Однопараметрическая модель Г. Раша. Однопараметрическая модель, которая часто называется простой логистической моделью, является одной из семейства логистических кривых, описанных Г. Рашем. Аналитическое задание однопараметрической модели представлено формулами (5.14) и (5.15).
Вид аналитического задания можно несколько изменить, записав функции Рi(Q) и Pj(b) следующим образом:
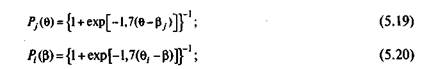
В первом случае вероятность правильного выполненияу'-го задания теста является возрастающей функцией от переменной. Это свойство функции легко интерпретируется и согласуется с практическим опытом педагога. Естественно ожидать, что чем больше уровень подготовки испытуемого, тем больше вероятность правильного выполнения иму-ro задания теста.
На рис. 5.19 изображена характеристическая кривая j- го задания теста, показывающая взаимосвязь между значениями независимой переменной 0 и величиной Pj(Q) приведена на рис. 5.19. Точке перегиба характеристической кривой соответствует значение 6= Р7, а Р, в этой точке равно 0,5.
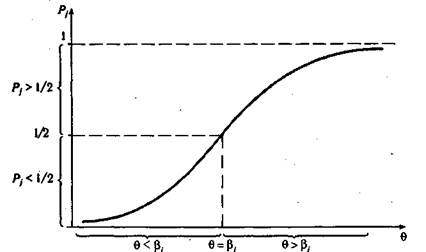
Рис. 5.19. Характеристическая кривая у-го задания теста
Таким образом, испытуемый с уровнем подготовки, равным трудности у-го задания теста, ответит на него правильно с вероятностью 0,5. Для испытуемых с уровнями знаний намного большими b, вероятность правильного ответа стремится к единице. Если же 0 расположено достаточно далеко от значения 0 = р. и слева от точки перегиба кривой, то вероятность правильного выполнения j-го задания теста стремится к нулю.
Разность Q — b обладает интересным свойством, позволяющим на репрезентативной выборке испытуемых реализовать идею инвариантности параметров вир. Для иллюстрации свойства достаточно рассмотреть ситуацию, когда испытуемый или группа испытуемых с уровнем подготовки Q, ответит на задание j с вероятностью Pj (рис. 5.20).

Рис. 5.20. Иллюстрация инвариантности оценок уровня подготовки испытуемых от трудности заданий теста
Увеличение трудности j-го задания теста на константу с (с > 0) вызовет смещение характеристической кривой вправо. С прежней вероятностью на это более трудное задание будет отвечать испытуемый с уровнем подготовки Qj + с. Так как
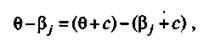
значения функции Pj (Q) не изменятся, что дает основание для вывода об относительной инвариантности уровня подготовки испытуемых от трудности заданий теста.
Вероятность правильного выполнения j-м испытуемым различных по трудности заданий Q+c является убывающей функцией переменной р. Это означает, что с ростом трудности заданий значения вероятности Р. (Р) будут уменьшаться. График функции называется индивидуальной кривой j-го испытуемого (рис: 5.21).
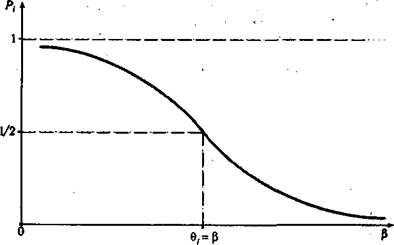
Рис. 5.21. Индивидуальная кривая i-ro испытуемого
В точке перегиба кривой, соответствующей значению независимой переменной Qi = b, функция Pi(b) принимает значение Pt= 0,5. В процессе обучения по мере накопления знаний индивидуальная кривая испытуемого смещается вправо.
Если /-и ученик выполняет задание трудностью Р[ с вероятностью Р, (рис. 5.22), то задание трудностью bi + с (с > 0) с прежней вероятностью будет выполнять более подготовленный ученик: Qi + с (с > 0). Как и ранее, это соображение дает основание для вывода об инвариантности оценок параметров вир.
Эффект инвариантности оценок параметра трудности заданий от характера распределения испытуемых по уровню подготовки в тестируемой выборке учеников отражен на рис. 5.23.
Поскольку вдоль кривой откладываются доли правильных ответов на задания, которые не зависят от характера распределения группы тестируемых учеников, то форма характеристической кривой задания и ее положение получатся одними и теми же при шкалировании задания в первой слабой и во второй сильной группах.
Конечно, практика свидетельствует о том, что эффект инвариантности наблюдается далеко не всегда, а только в тех случаях, когда реальная статистика — доли правильных ответов учащихся на задания — лежит достаточно близко к теоретической кривой.
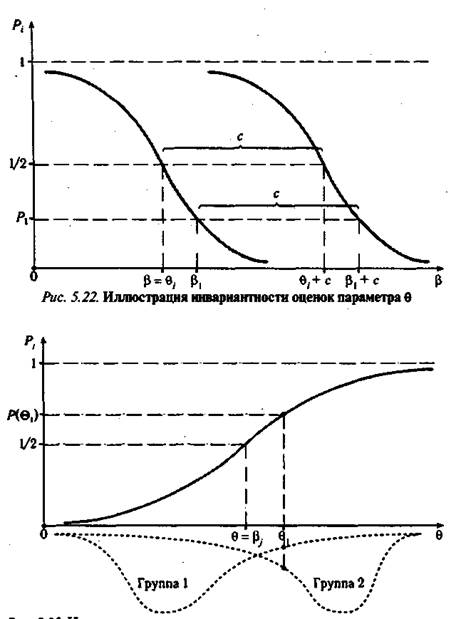
Рис. 5.23. Иллюстрация инвариантности оценок параметра трудности от уровня подготовленности тестируемой группы учеников
Причем чем ближе подходят точки распределения долей к кривой — графика функции Р., тем ярче проявляется инвариантность при шкалировании заданий теста, тем больше оснований для получения устойчивых значений параметра В. (j = 1,2,..., и) при создании теста.
Алгоритмы расчета оценок параметра испытуемых и трудности заданий теста. Для построения характеристических кривых заданий теста и индивидуальных кривых испытуемых необходимо знать значения параметров 9 и р. Оценка параметров проводится в предположении нормальности распределений эмпирических данных тестирования по множеству как испытуемых, так и заданий теста. Нормально распределенными считаются и значения латентных переменных. ;
Обычно в процессе разработки теста приходится оценивать оба параметра 0 и р. В случае использования готового теста с известными устойчивыми значениями параметра трудности, выраженными в логитах, задача сводится к оценке только значений параметра в
[31].
Алгоритм расчета значений параметров Эйр можно разбить на ряд этапов.
Первый этап. На первом этапе производится подсчет дол ей правильных и неправильных ответов каждого испытуемого на все задания теста. Доля правильных ответов /-го ученика находится по формуле

где i = 1, 2,..., N; п — число заданий в тесте. Доля неправильных ответов

Например, для 1-го ученика из примера матрицы результатов тестирования в разд. 5.2 (см. табл. 5.3)
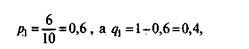
для второго р2 = 0,2, a q2 = 0,8 и т. д. Результаты подсчета долей для всех учеников выборки приводятся в табл. 5.12 совместно с данными по второму этапу.
Второй этап. Производится предварительная оценка значений параметра, характеризующего уровень подготовки учеников тести-
Таблица 5.12. Начальные значения логитов уровня подготовки испытуемых
| i | Xi | Доля правильных ответов i-го испытуемого pi | Доля неправильных ответов i-го испытуемого qi | Начальные оценки уровня подготовки в логитах Qi0 |
| 0,6 | 0,4 | 0,4055 | ||
| 0,2 | 0,8 | -1,3863 | ||
| 0,1 | 0,9 | -2,1972 | ||
| 0,9 | 0,1 | 2,1972 | ||
| 0,4 | 0,6 | -0,4055 | ||
| 0,4 | 0,6 | -0,4055 | ||
| 0,5 | 0,5 | 0,0000 | ||
| 0,4 | 0,6 | -0,4055 | ||
| 0,9 | 0,1 | 2,1972 | ||
| 0,6 | 0,4 | 0,4055 |
руемой группы. Начальные значения параметра оцениваются в логитах. Логит уровня подготовки/-го ученика 9/ находят по формуле

где pj и q. — доли правильных и неправильных соответственно ответов i-го ученика на задания теста.
Например, для 1 -го ученика начальное значение логиста уровня подготовки будет

Доли правильных и неправильных ответов учеников, а также начальные значения параметра Qi0 (i= 1,2,..., N) приведены в табл. 5.12.
Третий этап. На третьем этапе подсчитываются доли правильных gi и неправильных я ответов на каждое задание теста:

где rj— количество правильных ответов на j-е задание теста,. i= 1, 2,..., п, и п — число заданий в тесте.
Например, для 1-го задания из матрицы в табл. 5.3
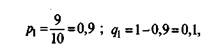
для 2-го р2= 0,8, а д2= 0,2 и т. д.
Доли правильных и неправильных ответов для всех заданий приводятся в табл. 5.13, где задания ранжированы по убыванию чисел R,
Четвертый этап. Производится предварительная оценка значений параметра р, характеризующего трудность заданий теста. В качестве меры трудности заданий выбирается единица измерения, называемая логитом. По определению, логит трудности j-го задания равен
Таблица 5.13. Начальные значения логитов трудности заданий
| j | Rj | Доля правильных ответов на j-е задание | Доля неправильных ответов на j-е задание | Начальные оценки трудности заданий в логитах bj0, |
| 0,9 | 0,1 | -2,1072 | ||
| 0,8 | 0,2 | -1,3863 | ||
| 0,7 | 0,3 | -0,8473 | ||
| 0,6 | 0,4 | -0,4055 | ||
| 0,5 | 0,5 | 0,0000 | ||
| 0,5 | 0,5 | 0,0000 | ||
| 0,4 | 0,6 | 0,4055 | ||
| 0,3 | 0,7 | 0,8473 | ||
| 0,2 | 0,8 | 1,3863 | ||
| 0,1 | 0,9 | 2,1972 |

где р. и q. — доли правильных и неправильных ответов на j-е задание теста;

Начальные значения логитов трудности приводятся в табл. 5.13. Теоретически начальные значения параметров вир могут меняться в интервале 
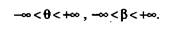
Но практически при Qi - bi < -5 значения Pij близки к нулю.
Аналогичная пограничная ситуация наблюдается, когда Q – bj > 5,
тогда Р.. очень близка к единице. Для иллюстрации утверждения соотношение между разностью в - Р и соответствующим значением вероятности правильного ответа по однопараметрической модели (5.14) приводится в табл. 5.14.
Пятый этап. На пятом этапе подсчитываются средние значения логитов уровня подготовки и логитов трудности заданий теста.
Среднее значение 0 для множества Qi0 (i= 1, 2,..., N) подсчитывают по формуле

где Q —начальные значения уровня подготовки i- го ученика; N- число учеников в группе.
Среднее значение р для множества b°i (i = 1> 2,..n., и) будет
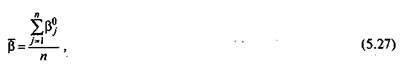
Таблица 5.14. Соотношение между значениями разности и вероятностью правильного ответа
| Оценка уровня подготовки Q | Оценка трудности заданий теста bi | Разность Qi - bj | Вероятность правильного ответа PijJ |
| 0,99 | |||
| 0,98 | |||
| 0,95 | |||
| 0,88 | |||
| 0,73 | |||
| 0,50 | |||
| -1 | 0,27 | ||
| -2 | 0,12 | ||
| -3 | 0,05 | ||
| -4 | 0,02 | ||
| -5 | 0,01 |
где Рj — начальные значения логитов трудности заданий; «— число заданий теста.
Для рассматриваемого примера матрицы
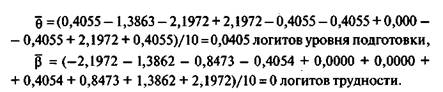
Шестой этап. После завершения пятого этапа оценки каждого из параметров Q b b будут выражены в интервальной шкале, но с разными значениями средних и разными стандартными отклонениями. На шестом этапе начальные значения логитов уровней подготовки и трудности заданий теста переводятся в единую интервальную шкалу стандартных оценок. Стандартизация достигается с помощью ряда специальных преобразований [6], для осуществления которых вычисляются:
— дисперсия по множеству значений Qi0 (i= 1, 2,..., N)

— дисперсия по множеству р°. (/= 1, 2,..., n)

- поправочные коэффициенты

Оценки параметров 9 и р в единой интервальной шкале находятся по формулам

где все обозначения прежние, а параметры вир имеют оценки Qi (i=1,2,..., N) и bj(j = 1, 2,...,n) в стандартной интервальной шкале.
Роль двух последних формул в развитии современной теории тестов трудно переоценить, хотя на первый взгляд они имеют узкую практическую направленность. Эти формулы позволяют преодолеть ряд существенных недостатков классической теории тестов, поскольку с их помощью можно получить объективные оценки параметров испытуемых и заданий, не зависящие друг от друга и выраженные в единой интервальной шкале.
Для рассматриваемого примера по данным табл. 5.12
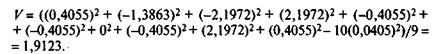
По данным табл. 5.13

Логит уровня подготовки 1-го испытуемого в стандартной шкале будет Qi = 1,6108 • 0,4055 = 0,6531 логита.
Оценки уровня подготовки группы испытуемых для данных рассматриваемого примера матрицы (см. табл. 5.3) помещены в табл. 5.15.
Оценка трудности 1-го задания в стандартной шкале

Таблица 5.15. Стандартные оценки уровня подготовки испытуемых
| i | Вектор уровня подготовки испытуемых Qi (в логитах) |
| 0,6531 | |
| -2,2329 | |
| -3,5392 | |
| 3,5392 | |
| -0,6531 | |
| -0,6531 | |
| -0,6531 | |
| 3,5392 | |
| 0,6531 |
Стандартные оценки параметра трудности заданий для рассматриваемого примера матрицы приводятся в табл. 5.16.
Обращает на себя внимание тот факт, что рассматриваемый тест первоначально казался на редкость удачно сбалансированным по трудности, поскольку
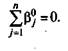
Как раз к этому эффекту обычно и стремятся разработчики нормативно-ориентированных тестов. Однако после перехода в интервальную шкалу логитов это соотношение изменилось, и

Таким образом, в тесте наблюдается избыточное количество трудных заданий, так как
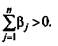
Таблица 5.16. Стандартные оценки трудности заданий теста
| j | Вектор уровня трудности заданий bj логитов |
| -3,5811 | |
| -2,2445 | |
| -1,3561 | |
| -0,6279 | |
| 0,0405 | |
| 0,0405 | |
| 0,7089 | |
| 1,4371 | |
| 2,3255 | |
| 3,6621 |
Например, для 1-го испытуемого с уровнем подготовки bi = 0,6531

Результаты подсчета ошибок измерения 9(. (/= 1, 2,..., N) для рассматриваемого примера приведены в табл. 5.17.
Восьмой этап. На восьмом этапе оценивается стандартная ошибка измерения Se(bj), которая вычисляется для каждого значения bj:
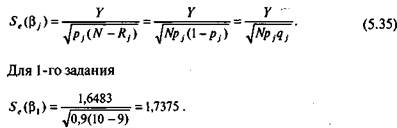
Таблица 5.17. Ошибки измерения параметра 6,
| Вектор уровня подготовки испытуемых 6, (в логитах) | Стандартная ошибка оценки уровня подготовки | |
| -3,5392 | 1,6979 | |
| -2,2329 | 1,2734 | |
| -0,6531 | 1,0398 | |
| -0,6531 | 1,0398 | |
| -0,6531 | 1,0398 | |
| 1,0188 | ||
| 0,6531 | 1,0398 | |
| 0,6531 | 1,0398 | |
| 3,5392. | 1,6979 | |
| 3,5392 | 1,6979 |
Для 10 заданий рассматриваемого примера матрицы стандартные ошибки оценок трудности заданий приводятся в табл. 5.18.
Анализ значений ошибок в табл. 5.17 и 5.18 указывает на нарастание ошибочного компонента в оценках параметров Q и b к концам распределения.
Хотелось бы напомнить еще раз о важном преимуществе полученных оценок параметров Q и b. Благодаря особенностям математического аппарата IRT проведенные расчеты обеспечивают объективные оценки уровня подготовки каждого испытуемого, не зависящие от трудности заданий теста. Отмеченное свойство инвариантности позволяет провести корректное сравнение результатов испытуемых, выполнивших различные по трудности задания теста и даже разные тесты.
Аналогичное преимущество существует в IRT и для оценок трудности заданий теста. Получаемые по алгоритмам значения параметра b инвариантны относительно уровня подготовки испытуемых в тестируемой группе.
Построение характеристических кривых заданий теста для однопараметрической модели. После подсчета значений параметров Q и b в шкале логитов приступают к построению характеристических кривых заданий теста. Анализ их взаимного расположения позволяет наметить пути дальнейшего совершенствования теста и сформировать систему заданий, наиболее эффективных для оценки уровня подготовки каждого испытуемого выборки.
Таблица 5.18. Стандартные ошибки оценок параметра трудности заданий
| j | Вектор уровня трудности заданий bj (в логитах) | Стандартная ошибка оценки трудности заданий |
| -3,5811 | 1,7375 | |
| -2,2445 | 1,3031 | |
| -1,3561 | 1,1375 | |
| -0,6279 | 1,0640 | |
| 0,0405- | 1,0425 | |
| 0,0405 | 1,0425 | |
| 0,7089 | 1,0640 | |
| 1,4371 | 1,1375 | |
| 2,3255 | 1,3031 | |
| 3,6621 | 1,7375 |
Процесс совершенствования теста начинается с удаления лишних заданий, нарушающих нормальный характер распределения значений р. Далее разработчику необходимо обратить внимание на случаи наложения характеристических кривых и избавиться от лишних заданий, которые ничего не дают для теста как совокупности работающих заданий возрастающей трудности.
Следующий важный шаг при коррекции теста связан с выделением «пустых» интервалов оси 0, где нет характеристических кривых. В тест необходимо добавить задания, соответствующие по трудности выделенным интервалам на оси латентной переменной 9. В идеале характеристические кривые должны заполнять более или менее равномерно практически весь интервал (-5; +5) шкалы логитов. Причем заданий средней трудности должно быть намного больше, чем на краях распределения. Заполнение всех «пустых» интервалов может привести к неоправданному увеличению длины теста, что в конечном счете сделает тестирование неэффективным и приведет к ухудшению, а не к улучшению теста. Поэтому решение о добавлении недостающих заданий, равно как и об устранении лишних, пока не является окончательным. Его можно рассматривать лишь как предварительный этап в создании теста, разумный после первоначального сбора эмпирических данных, когда число заданий в тесте намного превышает планируемое и рассчитано именно на такую предварительную работу.
Для более обоснованного решения необходим дополнительный анализ тестируемого контингента. Если группа гомогенна по уровню подготовки и большинство значений в расположено на небольшом интервале оси латентной переменной, то основную часть заданий следует сгруппировать на этом интервале, расположив характеристические кривые достаточно плотно. В случае гетерогенной по подготовке выборки испытуемых значения параметра трудности должны охватывать больший интервал оси 6, а характеристические кривые заданий могут быть расположены довод i-но далеко друг от друга.
При построении характеристической кривой задания его трудность считается параметром, a G — независимой переменной, значения которой выбираются произвольно. Ординаты характеристических кривых — значения функции Р. — подсчитываются по формуле (5.14). Например, для 1-го задания с трудностью bj = - 3,5811 логита характеристическая функция имеет вид:
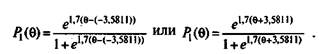
Для построения графика функции /^(8) необходимо выбрать несколько значений независимой переменной 6, а затем вычислить значения функции P{(Q). Эти значения приводятся в табл. 5.19.
Таблица 5.19. Значения функции Рi(Q)
| Q | Pi(Q) |
| -5,0 | 0,0000=0 |
| -4,5 | 0,1733=0,2 |
| -4,0 | 0,3291=0,3 |
| -3,5 | 0,5344=0,5 |
| -3,0 | 0,7287=0,7 |
| -2,5 | 0,8627=0,9 |
| -2,0 | 0,9363=0,9 |
После нанесения значений функции на координатной плоскости и соединения полученных точек график функции P{(Q) имеет вид (рис. 5.24).
Характеристические кривые 10 заданий для данных табл. 5.3 приведены на рис. 5.25. Как правило, для полного решения задачи отбора наиболее эффективных заданий при конструировании теста однопараметрической модели Г. Раша оказывается недостаточно. Это связано с определенными ограничениями, накладываемыми на крутизну кривых заданий в рамках данной модели. В частности, она считается одинаковой у всех кривых, что, конечно, обеспечивает определенную простоту в практических приложениях модели Г. Раша, но вместе с тем является и недостатком. Этот недостаток особенно заметен, когда нужно отдать предпочтение одному из заданий равной трудности. Если анализ проводится без привлечения двухпараметрической модели, то можно легко
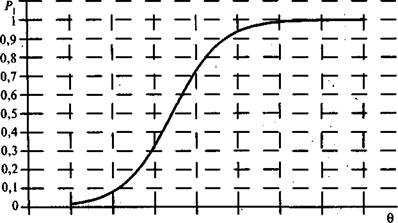
Рис. 5.24. Характеристическая кривая 1-го задания теста
прийти к неверному решению и существенно снизить надежность и валидность теста, удалив задания с более крутыми характеристическими кривыми, а оставив с более пологой.
Двухпараметрическая модель А. Бирнбаума. Формулу (5.16) для условной вероятности правильного выполнения j-го задания теста испытуемыми с различными значениями 0 в случае двухпараметрической модели А. Бирнбаума можно переписать в виде
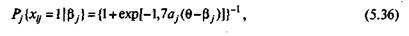
где кроме прежних обозначений вводится новое а, идя 2-го параметра j-го задания теста.
При геометрической интерпретации 1-й параметр b можнорассматривать как характеристику положения кривой i-го задания относительно оси 0. Второй параметр а, связан с крутизной кривой задания в точке ее перегиба. А именно значение а, прямо пропорционально тангенсу угла наклона касательной к характеристической кривой задания теста в точке Q=bj. (рис. 5.26). Это означает, что более крутые кривые соответствуют большим значениям а, соответственно для пологих кривых aj - 0.
На рис. 5.27 приведены характеристические кривые трех заданий одинаковой трудности (b = b1 = b2= b3), но разной крутизны. Для сравнительной характеристики качества заданий при дифференциации знаний испытуемых группы лучше рассмотреть заметно различающиеся по крутизне кривые 1 -го (кривая 7) и 3-го (кривая J) заданий теста.
Date: 2016-11-17; view: 350; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |