Критерий устойчивости Михайлова.

Из выражения (5.10) следует критерий устойчивости Михайлова, согласно которому изменение аргумента характеристического вектора определяется по годографу вектора, записанному в виде

D(jw) = X(w) + jY(w) = D(w)e^jy(w) , (5.11)

где X(w) и Y(w) действительная и мнимая части характеристического вектора, а D(w) и y(w) его модуль и аргумент.

Формулировка критерия. Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента функции D(jw) при изменении w от 0 до ¥ равнялось бы n .

Другими словами, система устойчива, если годограф характеристического вектора (кривая Михайлова), начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n - порядок характеристического уравнения системы.

На рис.5.8 приведены примеры годографов для устойчивой и неустойчивой систем.

а) б)

Рис. 5.8. Кривая Михайлова:

а - устойчивой системы 3-го порядка; б - неустойчивой системы

Если годограф проходит через начало координат, то система находится на границе устойчивости. В этом случае

X(w) = 0 и Y(w) = 0. (5.12)

Из этих уравнений можно определить значения параметров, при которых система находится на границе устойчивости.

Пример. Исследуем на устойчивость систему, рассмотренную в предыдущем примере, характеристический полином которой имеет вид: D(p) = T₁ T₂ p³ + (T₁ + T₂ )p² + p + k.

Решение. Найдем годограф характеристического вектора

D(jw) = T₁ T₂ (jw)³ + (T₁ + T₂ )(jw)² + jw + k.

Откуда

Re D(jw) = X(w) = k - (T₁ + T₂ )w²;

Im D(jw) = Y(w) = w - T₁ T₂ w³.

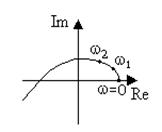
Для того, чтобы система 3-го порядка была устойчива, кривая Михайлова должна последовательно проходить три квадранта (рис.5.9).

Рис. 5.9. Кривая Михайлова

Найдем условие устойчивости из требования чередования корней

0=w₁<w₂<w₃.

Корень w₂ находится из уравнения X(w)=0, откуда

.

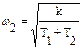Отсюда первое условие устойчивости: k>0.

Корень w₃ находится из уравнения Y(w)=0, откуда

.

Подставляя эти значения в требуемое условие w₂<w₃, получаем второе условие устойчивости системы

k < ( + ),

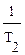которое, конечно, совпадает с полученным ранее условием устойчивости по критерию Гурвица.