
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Однофакторный дисперсионный анализ
Имеется количественная переменная у, определяемая качественной переменной, иначе фактором, принимающим р дискретных значений (уровней). Так, фактором может быть «поставщик», уровнями – определенные фирмы-поставщики, переменной у – срок службы поставляемого товара. В качестве исходных данных выступает выборка, содержащая ряд наблюдений на каждом из уровней (по нескольку экземпляров определенного товара от каждого поставщика). Необходимо ответить на вопрос – различаются ли по сроку службы объекты от разных поставщиков.
Модель однофакторного анализа:  , (5.1)
, (5.1)
где  – наблюденные значения, Ni – объем выборки для i -го уровня фактора. Параметр m обозначает некоторую точку отсчета, ai – эффект (вклад) i -го уровня фактора, uij – независимые, нормально распределенные случайные возмущения, удовлетворяющие предпосылке 5 классической регрессии.
– наблюденные значения, Ni – объем выборки для i -го уровня фактора. Параметр m обозначает некоторую точку отсчета, ai – эффект (вклад) i -го уровня фактора, uij – независимые, нормально распределенные случайные возмущения, удовлетворяющие предпосылке 5 классической регрессии.
Модель (5.1) не позволяет однозначно оценить параметры, поскольку можно добавить к m и вычесть из ai произвольную константу. Неоднозначность снимается условием репараметризации N 1 a 1+ N 2 a 2+…+ Npap= 0. (5.2)
Оценивание параметров производится по методу наименьших квадратов (МНК). Для минимизации остаточной суммы квадратов  найдем первые производные:
найдем первые производные:
 ;
;
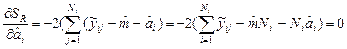 .
.
Обозначим 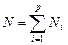 . Из выражений для производных с учетом (5.2) получаем:
. Из выражений для производных с учетом (5.2) получаем:
 . (5.3)
. (5.3)
(Точка на месте индекса означает усреднение по этому индексу.)
Результаты измерений принято представлять в виде табл.11.
Таблица 11
| Уровни фактора | Наблюдения | Сумма внутри уровня | Среднее по уровню | ||

| 
| 
| 
|  1× 1×
| |

| 
| 
| 
| 
| 
|
| р | 
| 
| 
| 
|  p. p.
|
- Проверка гипотез в однофакторном ДА.
В ДА основной интерес представляет не столько сами оценки, сколько их сравнение и, в первую очередь, проверка гипотезы Н 0: а 1= а 2=…= ар= 0, означающей одинаковость, неразличимость, воздействий всех р уровней. Со статистической точки зрения задачу ДА можно сформулировать так: для каждой из р генеральных совокупностей получено по выборке объемом Ni и необходимо сопоставить р значений выборочных средних.
ДА базируется на разложении общей суммы квадратов S 0 отклонений наблюдений  от общего среднего
от общего среднего  на составляющие, связанные с рассеянием между уровнями S му и рассеянием внутри отдельных уровней S ву:
на составляющие, связанные с рассеянием между уровнями S му и рассеянием внутри отдельных уровней S ву:
 , S му=
, S му=  , S ву=
, S ву=  .
.
Подобное разложение получается следующим образом. Обе части тождества 
возводят в квадрат и суммируют по i и j:
 (5.4)
(5.4)
Последнее слагаемое в правой части формулы (5.4) обращается в нуль в силу выполнения следующей очевидной цепочки равенств:

 .
.
Соотношение (5.4) приобретает вид S 0= S му+ S ву. Суммы S 0 ,Sму ,Sву имеют N- 1, p -1, N - p степеней свободы соответственно. Если имеет место проверяемая гипотеза Н 0, то каждое из отношений:

может служить оценкой дисперсии s2 случайных возмущений. В силу нормальности возмущений отношение  имеет F -распределение. Полученные значения представляют в виде табл.12.
имеет F -распределение. Полученные значения представляют в виде табл.12.
Таблица 12
| Источник изменчивости | Сумма квадратов | ЧСС | Среднее | F- отношение |
| Между уровнями | S му | p -1 | 
| Fр = 
|
| Внутри уровней | S ву | N-p | 
| |
| S 0 | N -1 |
Гипотеза Н 0: а 1= а 2=…= ар= 0 отвергается при выбранном уровне надежности (обычно, 95%), если F р >F Т, где F Т – табличное значение F -распределения при ЧСС числителя и знаменателя p -1 и
N-p соответственно. При F р £F Т делается вывод, что результаты наблюдений не противоречат гипотезе Н 0.
- Схема двухфакторного анализа.
Исследуемая переменная у определяется теперь двумя факторами A и В с p и q уровнями соответственно. На каждой из pq комбинаций уровней доступно по одному наблюдению. Для N=pq выборок единичного объема постулируется модель  ,
,
где m, ai, bj – параметры, uij – случайная компонента с теми же свойствами, что и в однофакторном ДА. Условий репараметризации здесь два:  .
.
Применяя МНК, находят оценки параметров:  ,
,  ,
,
 .
.
Основная задача двухфакторного ДА – проверка равенства нулю параметров ai и bj, т.е. проверка гипотез: НА: а 1=а2=…= ар =0 и НВ: b 1= b 2=…= bq= 0.
Как и в однофакторном ДА, общую сумму квадратов S 0 отклонений от общего среднего можно разложить на составляющие – теперь уже три: SA =  , S B =
, S B =  , обусловленные изменчивостью между уровнями факторов А и В соответственно, плюс слагаемое
, обусловленные изменчивостью между уровнями факторов А и В соответственно, плюс слагаемое  , связанное со случайной составляющей (экспериментальная ошибка).
, связанное со случайной составляющей (экспериментальная ошибка).
Схема вывода соотношения S 0 =SA+SB+SR (5.5) та же, что и в однофакторном ДА.
За основу положено тождество:  .
.
Исходные данные и результаты двухфакторного ДА принято представлять в виде табл.13 и 14.
Таблица13
| Уровни фактора А | Уровни фактора В | Среднее по строкам |
| 1 2 … q | ||
 p
p
|   … … 
  … … 
  
  … … 
| 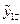



|
| Среднее по столбцам |   … … 
| 
|
Таблица 14
| Источник изменчивости | Сумма квадратов | ЧСС | Среднее квадратов | F -отношение |
| Фактор А | SA | p -1 | 
| 
|
| Фактор В | SB | q -1 | 
| 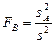
|
| Ошибка | SR | (p -1)´(q -1) | 
| |
| S 0 | pq -1 |
Гипотеза НА (НВ) считается приемлемой, если FA £ F Т А (FВ £ F Т В), где F Т А, F Т В – табличные значения F -распределения с ЧСС числителя и знаменателя в соответствии с табл.14.
- Экспериментальные критерии планирования эксперимента.
Все многообразие критериев планирования эксперимента можно разбить на две большие группы
Вторую группу составляют критерии, зародившиеся в практике планирования эксперимента и ориентированные на удобство расчетов и организации проведения экспериментов (критерии ортогональности и композиционности).
Смысл перечисленных критериев можно пояснить, используя понятие эллипсоида рассеяния случайного вектора. Для случайного вектора а размерности 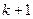 , ковариационная матрица которого есть cov a, эллипсоид рассеяния задается выражением
, ковариационная матрица которого есть cov a, эллипсоид рассеяния задается выражением  ,
,
описывающим эллипсоид в  -мерном пространстве с центром в точке Ма. Эта геометрическая фигура имеет такие размеры, что ковариационная матрица случайного вектора, равномерно распределенного в пределах эллипсоида, совпадает с матрицей cov a. Следовательно, чем больше рассеяние вектора относительно его математического ожидания, тем большие размеры имеет эллипсоид рассеяния.
-мерном пространстве с центром в точке Ма. Эта геометрическая фигура имеет такие размеры, что ковариационная матрица случайного вектора, равномерно распределенного в пределах эллипсоида, совпадает с матрицей cov a. Следовательно, чем больше рассеяние вектора относительно его математического ожидания, тем большие размеры имеет эллипсоид рассеяния.
Критерий ортогональности Критерий ортогональности требует выбора плана  , обеспечивающего диагональность информационной матрицы. Использование этого критерия имеет целью упростить вычисления и обеспечить независимость оценок коэффициентов регрессии.
, обеспечивающего диагональность информационной матрицы. Использование этого критерия имеет целью упростить вычисления и обеспечить независимость оценок коэффициентов регрессии.
Критерий композиционности Критерий композиционности требует выбора плана, который включал бы в себя точки оптимального плана моделей более низкого порядка. Это обеспечивает сокращение числа опытов при поэтапном усложнении модели.
На практике желательно использовать планы, удовлетворяющие одновременно нескольким критериям. В общем случае такого сочетания свойств не наблюдается. В теории планирования эксперимента доказано, что непрерывный D -оптимальный план является также G -оптимальным. Условие D -оптимальности дискретного плана  имеет следующий вид:
имеет следующий вид:  . (6.2)
. (6.2)
Если для дискретного D -оптимального плана имеет место  , то этот план является также A -оптимальным.
, то этот план является также A -оптимальным.
Построение D -оптимальных планов является сложной вычислительной задачей. Аналитический путь здесь оказывается возможным в некоторых простейших случаях (полиномиальная модель от одной переменной, квадратичная регрессия от  переменных для стандартной области (гиперкуб)). В общем случае для построения D -оптимальных планов используются численные методы, связанные с минимизацией определителя матрицы С либо максимизацией определителя информационной матрицы F’F, что несомненно проще в вычислительном отношении.
переменных для стандартной области (гиперкуб)). В общем случае для построения D -оптимальных планов используются численные методы, связанные с минимизацией определителя матрицы С либо максимизацией определителя информационной матрицы F’F, что несомненно проще в вычислительном отношении.
- Теоретические критерии планирования эксперимента.
Все многообразие критериев планирования эксперимента можно разбить на две большие группы. Первую составляют критерии, непосредственно учитывающие точностные свойства получаемых оценок. Среди них можно выделить критерии, связанные с точностью нахождения коэффициентов регрессии (критерии A - и D -оптимальности), и критерии, требующие максимальной точности оценки выходной переменной (критерий G -оптимальности).
Смысл перечисленных критериев можно пояснить, используя понятие эллипсоида рассеяния случайного вектора. Для случайного вектора а размерности 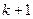 , ковариационная матрица которого есть cov a, эллипсоид рассеяния задается выражением
, ковариационная матрица которого есть cov a, эллипсоид рассеяния задается выражением  ,
,
описывающим эллипсоид в  -мерном пространстве с центром в точке Ма. Эта геометрическая фигура имеет такие размеры, что ковариационная матрица случайного вектора, равномерно распределенного в пределах эллипсоида, совпадает с матрицей cov a. Следовательно, чем больше рассеяние вектора относительно его математического ожидания, тем большие размеры имеет эллипсоид рассеяния.
-мерном пространстве с центром в точке Ма. Эта геометрическая фигура имеет такие размеры, что ковариационная матрица случайного вектора, равномерно распределенного в пределах эллипсоида, совпадает с матрицей cov a. Следовательно, чем больше рассеяние вектора относительно его математического ожидания, тем большие размеры имеет эллипсоид рассеяния.
Критерий А-оптимальности Поскольку точностной характеристикой вектора коэффициентов регрессии является ковариационная матрица, а критерии планирования желательно иметь в скалярной форме, то необходима некоторая свертка ковариационной матрицы. Критерий A-оптимальности в качестве такой свертки использует след матрицы  . Поскольку диагональные элементы матрицы С пропорциональны дисперсии оценок коэффициентов регрессии, то при минимизации следа матрицы С минимизируется, по сути дела, суммарная либо средняя дисперсия оценок коэффициентов модели:
. Поскольку диагональные элементы матрицы С пропорциональны дисперсии оценок коэффициентов регрессии, то при минимизации следа матрицы С минимизируется, по сути дела, суммарная либо средняя дисперсия оценок коэффициентов модели:  .
.
Известно, что сумма диагональных элементов матрицы равняется сумме её собственных значений. Поскольку квадраты длины осей эллипсоида рассеяния пропорциональны собственным значениям ковариационной матрицы, то критерий A-оптимальности требует минимизации диагонали параллелепипеда, описанного у эллипсоида рассеяния.
Критерий D-оптимальности Критерий D -оптимальности требует такого расположения точек в области планирования  , при котором определитель матрицы
, при котором определитель матрицы  имеет минимальную величину. Иными словами, план
имеет минимальную величину. Иными словами, план  D -оптимален, если
D -оптимален, если  .
.
Известно, что объем 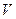 эллипсоида рассеяния пропорционален корню из величины определителя ковариационной матрицы, т.е.
эллипсоида рассеяния пропорционален корню из величины определителя ковариационной матрицы, т.е.  . С учетом (3.8) V ~
. С учетом (3.8) V ~  .
.
Чем меньше величина определителя, тем меньше, как правило, разброс оценок коэффициентов относительно их математических ожиданий. Исключением является случай, когда эллипсоид рассеяния имеет сильно вытянутую форму.
Критерий G-оптимальности План  G-оптимален, если он обеспечивает наименьшую величину максимальной дисперсии оценки зависимой переменной:
G-оптимален, если он обеспечивает наименьшую величину максимальной дисперсии оценки зависимой переменной:  .
.
- Регрессионный анализ факторного эксперимента.
Этапы факторного анализа Вычислительный аспект факторного анализа связан с определением факторного отображения В, дисперсий характерных факторов и оценкой значений общих факторов. Оценка этих параметров производится на основании экспериментальных данных, полученных в ходе наблюдений над N объектами (индивидами). Результаты наблюдений представляются в виде матрицы исходных данных, аналогичной (11.1). По матрице Х вычисляется корреляционная матрица R. Затем начинаются этапы собственно факторного анализа. Первый этап – оценка общностей. Если общности оценены, то по формуле (11.5) можно оценить характерности, а следовательно, и матрицу W, которая является диагональной согласно предпосылкам факторного анализа. Заменяя диагональные элементы матрицы R на оценки общностей, получают матрицу  , которая является информационной основой второго этапа выделения факторов. На этом этапе решают тем или иным способом матричное уравнение
, которая является информационной основой второго этапа выделения факторов. На этом этапе решают тем или иным способом матричное уравнение  , получая в итоге ортогональную матрицу A. Возможно большое число матриц A, которые одинаково хорошо будут воспроизводить матрицу
, получая в итоге ортогональную матрицу A. Возможно большое число матриц A, которые одинаково хорошо будут воспроизводить матрицу  . Из них должна быть выбрана одна, что составляет содержание третьего этапа – вращения факторов. И, наконец, на последнем, четвертом, этапе оцениваются значения факторов для каждого объекта (индивида). На практике, однако, из-за большого объема вычислений часто ограничиваются первыми тремя этапами, причем первый и второй выполняются одновременно.
. Из них должна быть выбрана одна, что составляет содержание третьего этапа – вращения факторов. И, наконец, на последнем, четвертом, этапе оцениваются значения факторов для каждого объекта (индивида). На практике, однако, из-за большого объема вычислений часто ограничиваются первыми тремя этапами, причем первый и второй выполняются одновременно.
Выделение факторов. Выделение факторов предполагает установление числа и направления осей координат, соответствующих общим факторам, необходимым для отображения корреляции исходных переменных. С алгебраической точки зрения проблема факторов означает определение ранга матрицы А и оценивание ее элементов. Для решения задачи выделения факторов разработано достаточно много методов, однако основными в настоящее время следует признать два: метод главных факторов, наиболее широко употребляемый на практике, и метод максимального правдоподобия, имеющий прочный математико-статистический фундамент.
Метод главных факторов. Как следует из фундаментальной теоремы факторного анализа (11.3),  . Приравняем вначале W нулевой матрице. Получим матричное уравнение
. Приравняем вначале W нулевой матрице. Получим матричное уравнение  (11.6)
(11.6)
Матричное уравнение (11.6) имеет множество решений: любое ортогональное преобразование Т, переводящее матрицу В в G, т.е. G = ВТ, удовлетворяет (11.6). Действительно, в силу ортогональности Т имеет место  и, значит,
и, значит,  . Подставляя выражение для В в (11.6), получаем
. Подставляя выражение для В в (11.6), получаем
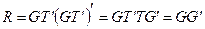 , поскольку T′T=I.
, поскольку T′T=I.
Как известно из линейной алгебры, ортогональное преобразование системы координат означает поворот системы как целого на некоторый угол вокруг начала координат. Выделяя некоторое предпочтительное направление и фиксируя тем самым угол поворота системы координат, можно обойти проблему неоднозначности решения системы (11.6).
Вернемся на время к методу главных компонент. Выбор осей координат здесь подчинен определенному требованию: каждая следующая ось ориентирована по направлению максимальной дисперсии в пространстве, ортогональном предыдущим главным компонентам. Матрица весовых коэффициентов А при этом составлена из собственных векторов ковариационной (корреляционной R) матрицы. Следовательно,
 , (11.7)
, (11.7)
где  – диагональная матрицa с элементами, равными собственным значениям корреляционной матрицы. Умножая (11.7) на
– диагональная матрицa с элементами, равными собственным значениям корреляционной матрицы. Умножая (11.7) на  справа и учитывая ортогональность A, а значит
справа и учитывая ортогональность A, а значит  , получаем:
, получаем:  .
.
Обозначим через  матрицу порядка
матрицу порядка 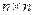 , элементы которой равняются квадратному корню из соответствующих элементов матрицы Λ. Перейдем от A к
, элементы которой равняются квадратному корню из соответствующих элементов матрицы Λ. Перейдем от A к  . Выражение для R примет вид:
. Выражение для R примет вид:
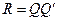 . (11.8)
. (11.8)
Сравнивая (11.6) и (11.8), получаем, что в качестве оценки матрицы В можно взять матрицу  .
.
Таким образом, матрица факторных нагрузок получается из матрицы, составленной из собственных векторов корреляционной матрицы исходных признаков, с последующим умножением элементов собственного вектора, отвечающего i -му собственному значению 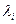 на
на 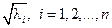 .
.
Матрицы B и Q имеют разный порядок:  у В и
у В и 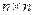 у Q, поэтому правильнее говорить, что оценкой будут первые m столбцов матрицы Q.
у Q, поэтому правильнее говорить, что оценкой будут первые m столбцов матрицы Q.
Посчитав матрицу W равной нулю, мы для оценки матрицы B воспользовались моделью главных компонент. Строго говоря, под методом главных факторов понимают способ расчета, принятый в методе главных компонент, но примененный к матрице  (оценка общностей рассматривается ниже).
(оценка общностей рассматривается ниже).
0ценка числа общих факторов.
…….
Метод максимального правдоподобия. В этом методе по выборочной корреляционной матрице  исходных признаков ищутся состоятельные и эффективные оценки неизвестных параметров − элементов матриц В и W для генеральной совокупности. При построении функции максимального правдоподобия существенно используются предпосылки факторного анализа. Максимизация функции правдоподобия приводит к множественности результатов. Неоднозначность обходится требованием, чтобы матрица
исходных признаков ищутся состоятельные и эффективные оценки неизвестных параметров − элементов матриц В и W для генеральной совокупности. При построении функции максимального правдоподобия существенно используются предпосылки факторного анализа. Максимизация функции правдоподобия приводит к множественности результатов. Неоднозначность обходится требованием, чтобы матрица
 (11.9)
(11.9)
имела диагональный вид. Это условие соответствует требованию метода главных факторов о взаимной ортогональности факторов и их ориентации по направлению максимума дисперсии.
Система (11.9) может быть приведена к виду, удобному для вычислений итерационным путем:
 . (11.10)
. (11.10)
Скорость сходимости итерационной процедуры является весьма медленной и зависит от начального приближения B и W.
В методе максимального правдоподобия проблема определения числа факторов также существует. Пусть расчеты по (11.10) проведены для m общих факторов. Для проверки гипотезы о существовании m общих факторов можно воспользоваться критерием 
c  степенями свободы.
степенями свободы.
В этой формуле  – определитель матрицы корреляций, воспроизведенных с помощью m общих факторов. Если вычисленное значение критерия превышает табличное значение
– определитель матрицы корреляций, воспроизведенных с помощью m общих факторов. Если вычисленное значение критерия превышает табличное значение  при выбранном уровне значимости, то необходимо выделить факторов больше, чем m, по крайней мере, m+ 1.
при выбранном уровне значимости, то необходимо выделить факторов больше, чем m, по крайней мере, m+ 1.
- Совместность оценок дробного факторного эксперимента.
Дробный факторный эксперимент (ДФЭ) Из-за показательного роста числа экспериментов с увеличением размерности пространства  ПФП оказываются практически неприемлемыми при больших
ПФП оказываются практически неприемлемыми при больших  . Однако из матрицы ПФП
. Однако из матрицы ПФП  может быть отобрана некоторая часть, называемая дробным факторным планом (ДФП), которая сохраняет свойство ортогональности. Правило построения ДФП состоит в следующем. Задается порядок дробности
может быть отобрана некоторая часть, называемая дробным факторным планом (ДФП), которая сохраняет свойство ортогональности. Правило построения ДФП состоит в следующем. Задается порядок дробности  . Из
. Из  входных переменных отбирают n - p переменных (их называют основными), и для них строят полный факторный план
входных переменных отбирают n - p переменных (их называют основными), и для них строят полный факторный план  . Этот план затем дополняют
. Этот план затем дополняют  столбцами, соответствующими оставшимся переменным. Для определения способа образования этих столбцов вводится понятие генератора (генерирующего соотношения) плана. Генератор представляет собой произведение граничных значений (
столбцами, соответствующими оставшимся переменным. Для определения способа образования этих столбцов вводится понятие генератора (генерирующего соотношения) плана. Генератор представляет собой произведение граничных значений ( ) основных переменных, определяющее граничные значения элементов каждого из дополнительных
) основных переменных, определяющее граничные значения элементов каждого из дополнительных  столбцов матрицы плана. Так, для построения линейной модели от трех переменных
столбцов матрицы плана. Так, для построения линейной модели от трех переменных  можно воспользоваться ДФП типа
можно воспользоваться ДФП типа  с генератором
с генератором  :
:

Чем выше размерность пространства  , тем большее число генераторов плана можно предложить. Целесообразно выбирать такие из них, которые соответствуют незначимым взаимодействиям. Действительно, в состав базисных функций входят и левая и правая части генератора и, поскольку от эксперимента к эксперименту они меняются одинаковым образом, различить эффекты, соответствующие частям генератора, не представляется возможным. Так, если в качестве генератора выбрано соотношение
, тем большее число генераторов плана можно предложить. Целесообразно выбирать такие из них, которые соответствуют незначимым взаимодействиям. Действительно, в состав базисных функций входят и левая и правая части генератора и, поскольку от эксперимента к эксперименту они меняются одинаковым образом, различить эффекты, соответствующие частям генератора, не представляется возможным. Так, если в качестве генератора выбрано соотношение 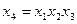 , то получить раздельные оценки для
, то получить раздельные оценки для  и
и  нельзя. Соответствующий ДФП позволяет оценить лишь суммарное воздействие линейного фактора
нельзя. Соответствующий ДФП позволяет оценить лишь суммарное воздействие линейного фактора 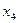 и тройного взаимодействия
и тройного взаимодействия  . Подобные оценки называют смешанными. Однако, если взаимодействие незначимо, т.е.
. Подобные оценки называют смешанными. Однако, если взаимодействие незначимо, т.е.  , то
, то  будет практически несмешанной оценкой. Для определения порядка смешивания вводят понятие контраста плана. Контраст – это генерирующее соотношение, задающее элементы столбца свободного члена матрицы
будет практически несмешанной оценкой. Для определения порядка смешивания вводят понятие контраста плана. Контраст – это генерирующее соотношение, задающее элементы столбца свободного члена матрицы 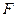 . (Со свободным членом уравнения регрессии связывается фиктивная переменная
. (Со свободным членом уравнения регрессии связывается фиктивная переменная  , тождественно равная единице.) Контраст получают из генерирующего соотношения умножением на переменную, стоящую слева от знака равенства. Для ДФП с генератором
, тождественно равная единице.) Контраст получают из генерирующего соотношения умножением на переменную, стоящую слева от знака равенства. Для ДФП с генератором 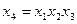 контраст есть
контраст есть 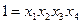 , так как
, так как 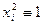 . Чтобы определить, с какими переменными или взаимодействиями смешана оценка некоторой данной переменной, необходимо умножить обе части контраста на эту переменную. При этом получают порядок смешивания оценок коэффициентов при использовании данного плана.
. Чтобы определить, с какими переменными или взаимодействиями смешана оценка некоторой данной переменной, необходимо умножить обе части контраста на эту переменную. При этом получают порядок смешивания оценок коэффициентов при использовании данного плана.
Пусть, к примеру, исследуется объект из трех переменных  полная модель которого есть
полная модель которого есть
 (В выражении (6.3) и далее случайное возмущение опускается.) В ходе исследования было решено ограничиться линейным (по переменным) описанием
(В выражении (6.3) и далее случайное возмущение опускается.) В ходе исследования было решено ограничиться линейным (по переменным) описанием
 , (6.4)
, (6.4)
что дало основание воспользоваться ДФЭ  с генератором
с генератором  с определяющим контрастом
с определяющим контрастом  . Порядок смешивания для переменных
. Порядок смешивания для переменных  следующий:
следующий:  ,
,  ,
,  . (6.5)
. (6.5)
С учетом (6.5) сгруппируем подобные члены в модели (6.3):  . (6.6)
. (6.6)
Сравнивая (6.6) и (6.4), видим, что при оценивании линейной модели (6.4) получаются не чистые оценки свободного члена  и линейных эффектов
и линейных эффектов  а оценки комбинаций, включающих двойные и тройные (для свободного члена) эффекты:
а оценки комбинаций, включающих двойные и тройные (для свободного члена) эффекты:  .
.
Таким образом, платой за сокращение числа экспериментов стала совместность оценок. Если же поставить дополнительно четыре эксперимента с генератором  , то получим оценки
, то получим оценки
 .
.
Восемь оценок  дают возможность получить раздельные оценки эффектов. Так,
дают возможность получить раздельные оценки эффектов. Так,  есть оценка
есть оценка  , а
, а  – оценка
– оценка  и так далее. Это и понятно, поскольку две серии экспериментов с генераторами
и так далее. Это и понятно, поскольку две серии экспериментов с генераторами  и
и  дают вкупе полный факторный эксперимент, который обеспечивает раздельное оценивание коэффициентов.
дают вкупе полный факторный эксперимент, который обеспечивает раздельное оценивание коэффициентов.
В отсутствии априорной информации о значимости взаимодействий предпочтение отдается генераторам, отвечающим взаимодействиям высокого порядка, поскольку коэффициенты регрессии при них по абсолютной величине, как правило, меньше.
К достоинствам факторных планов следует отнести их хорошие точностные свойства. Легко доказать, что они являются D-, G-, A - оптимальными. К примеру, у ПФП  , используемого для оценки коэффициентов модели вида
, используемого для оценки коэффициентов модели вида  , матрица плана X и матрица значений базисных функций F имеют вид:
, матрица плана X и матрица значений базисных функций F имеют вид:
 ,
,  .
.
Отсюда  , а
, а  . Левая часть выражения (6.2) примет вид
. Левая часть выражения (6.2) примет вид  , поскольку
, поскольку  . Максимум этой формы достигается в вершинах квадрата:
. Максимум этой формы достигается в вершинах квадрата:  ,
,  и равняется четырем. Число оцениваемых коэффициентов (k +1) также четыре. Следовательно, условие (6.2) выполняется.
и равняется четырем. Число оцениваемых коэффициентов (k +1) также четыре. Следовательно, условие (6.2) выполняется.
- D-оптимальные планы на отрезке.
- Связь D- и G-Оптимального планирования.
Критерий D-оптимальности Критерий D -оптимальности требует такого расположения точек в области планирования  , при котором определитель матрицы
, при котором определитель матрицы  имеет минимальную величину. Иными словами, план
имеет минимальную величину. Иными словами, план  D -оптимален, если
D -оптимален, если  .
.
Известно, что объем 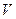 эллипсоида рассеяния пропорционален корню из величины определителя ковариационной матрицы, т.е.
эллипсоида рассеяния пропорционален корню из величины определителя ковариационной матрицы, т.е.  . С учетом (3.8) V ~
. С учетом (3.8) V ~  .
.
Чем меньше величина определителя, тем меньше, как правило, разброс оценок коэффициентов относительно их математических ожиданий. Исключением является случай, когда эллипсоид рассеяния имеет сильно вытянутую форму.
Критерий G-оптимальности План  G-оптимален, если он обеспечивает наименьшую величину максимальной дисперсии оценки зависимой переменной:
G-оптимален, если он обеспечивает наименьшую величину максимальной дисперсии оценки зависимой переменной:  .
.
На практике желательно использовать планы, удовлетворяющие одновременно нескольким критериям. В общем случае такого сочетания свойств не наблюдается. В теории планирования эксперимента доказано, что непрерывный D -оптимальный план является также G -оптимальным. Условие D -оптимальности дискретного плана  имеет следующий вид:
имеет следующий вид:  . (6.2)
. (6.2)
Если для дискретного D -оптимального плана имеет место  , то этот план является также A -оптимальным. Построение D -оптимальных планов является сложной вычислительной задачей. Аналитический путь здесь оказывается возможным в некоторых простейших случаях (полиномиальная модель от одной переменной, квадратичная регрессия от
, то этот план является также A -оптимальным. Построение D -оптимальных планов является сложной вычислительной задачей. Аналитический путь здесь оказывается возможным в некоторых простейших случаях (полиномиальная модель от одной переменной, квадратичная регрессия от  переменных для стандартной области (гиперкуб)). В общем случае для построения D -оптимальных планов используются численные методы, связанные с минимизацией определителя матрицы С либо максимизацией определителя информационной матрицы F’F, что несомненно проще в вычислительном отношении.
переменных для стандартной области (гиперкуб)). В общем случае для построения D -оптимальных планов используются численные методы, связанные с минимизацией определителя матрицы С либо максимизацией определителя информационной матрицы F’F, что несомненно проще в вычислительном отношении.
- Экспериментальные методы одномерного поиска.
Рассматривается функция одной переменной y=f (x). Предпола-гается, что функция имеет только один экстремум (унимодальна); интервал поиска ограничен:  ; значения выходной переменной неслучайны. Поиск осуществляется последовательно путем сравнения значений целевой функции в двух точках, выбираемых определенным образом. Эффективность E поиска характеризуется степенью локализации области экстремума после N экспериментов и выражается отношением длины начального интервала к остаточному
; значения выходной переменной неслучайны. Поиск осуществляется последовательно путем сравнения значений целевой функции в двух точках, выбираемых определенным образом. Эффективность E поиска характеризуется степенью локализации области экстремума после N экспериментов и выражается отношением длины начального интервала к остаточному  , внутри которого находится экстремум целевой функции:
, внутри которого находится экстремум целевой функции:  .
.
Далее для определенности будем полагать, что ищется максимум функции.
Эквидистантные планы Начальный отрезок делится на (N -1) равных частей, опыты проводятся при значениях:
 . Поиск прекращается как только
. Поиск прекращается как только 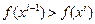 .
.
В зависимости от вида функции поиск прекращается при различных i, так что средняя эффективность составит E =(N –1)/2.
Метод деления отрезка пополам (метод последовательной дихотомии)
Эксперименты ставят парами в точках, отстоящих по обе стороны от середины отрезка. Координаты первой пары:
 где e – малая величина.
где e – малая величина.
Если 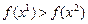 , то максимальное значение надо ожидать на отрезке
, то максимальное значение надо ожидать на отрезке  ; при
; при 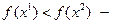 на отрезке
на отрезке  . Этот новый отрезок объявляется исходным, и далее процесс повторяется. Мера эффективности равна
. Этот новый отрезок объявляется исходным, и далее процесс повторяется. Мера эффективности равна  .
.
Заметим, что при наличии случайного компонента значение e не должно быть малым, что иллюстрируется рис.3.





 |




 x
x
Рис. 3. Метод деления отрезка пополам
Если в точке х 1 случайная компонента окажется отрицательной, а в точке х 2 положительной, и значительной по величине в обеих точках, результаты сравнения значений отклика в этих точках направят поиск в противоположную сторону, Вот почему применение метода деления отрезка пополам в этих условиях становится проблематичным.
Поиск с использованием чисел Фибоначчи Числа Фибоначчи задаются по следующим правилам:
 ,
, 

На первом шаге ставятся два эксперимента в точках x 1= a+ (b-a) q и x 2= b- (b-a) q при q=FN- 2 /FN, (6.10)
где N выбирается заранее.
При 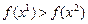 максимальное значение следует искать на отрезке
максимальное значение следует искать на отрезке  , при
, при 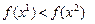 – на отрезке
– на отрезке  . На последующих шагах ставят по одному эксперименту, меняя q по закону
. На последующих шагах ставят по одному эксперименту, меняя q по закону  , где j – номер шага (j =2,3,…).
, где j – номер шага (j =2,3,…).
Легко показать, опираясь на определение чисел Фибоначчи, что одна из координат, подсчитанная по формулам, аналогичным (6.10), будет совпадать с одной из предыдущих точек. Далее происходит сравнение значений функций в этих двух точках и процесс повторяется. Мера эффективности метода составляет  .
.
Так, при N =10  =144, а значит с помощью 11 экспериментов можно локализовать экстремум в области, не превышающей 1% размера начальной области поиска. Этот метод существенно эффективнее предыдущего. К его недостатку можно отнести необходимость заранее задавать число экспериментов.
=144, а значит с помощью 11 экспериментов можно локализовать экстремум в области, не превышающей 1% размера начальной области поиска. Этот метод существенно эффективнее предыдущего. К его недостатку можно отнести необходимость заранее задавать число экспериментов.
Метод золотого сечения Этот метод базируется на методе Фибоначчи и не требует предварительного задания числа экспериментов. В методе золотого сечения вместо величины  на каждом шаге используется ее предельное значение при
на каждом шаге используется ее предельное значение при 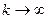 :
:  .
.
Мера эффективности метода 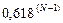 .
.
Date: 2016-06-07; view: 605; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |