
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретические сведения. На практике иногда встречаются интегралы, которые не выражаются через элементарные функции или подынтегральная функция задаётся таблицей или графиком
На практике иногда встречаются интегралы, которые не выражаются через элементарные функции или подынтегральная функция задаётся таблицей или графиком. В этих случаях интегралы находятся приближенными методами вычислений. Большинство методов приближенного вычисления интегралов предполагает, что подынтегральная функция на отрезке [a,b] задана табличными значениями:
yi = f(xi); где a <= x0 < x1 <... < xn <= b.
При этом разность xi - xi+1 = Dx называется элементарным отрезком.
Значение интеграла на отрезке [a,b] заменяется пределом суммы элементарных отрезков, умноженных на значение функции в одной из точек каждого элементарного отрезка:
Значение интеграла на отрезке [a,b] заменяется пределом суммы элементарных отрезков, умноженных на значение функции в одной из точек каждого элементарного отрезка:

где ki – некоторая точка на отрезке Dxi.
Геометрически каждый фрагмент суммы может быть представлен следующим рисунком.

Рисунок 1.1 – Геометрическое изображение фрагмента суммы интеграла
Точность вычисления интеграла зависит от формы представления «верхней» части этого фрагмента. Можно его представить прямоугольником по значению функции в точке xi, xi+1 или в средней точке (xi + xi+1)/2; либо трапецией – соединив прямой линией точки xi и xi+1; либо «верхнюю» часть заменяют известной зависимостью, например, параболой и т.д.
В зависимости от способа представления «верхней» части элементарного фрагмента существуют различные численные методы вычисления интеграла. Рассмотрим некоторые из них.
1.3.1 Вычисление интеграла с помощью прямоугольников
Известны три формулы вычисления прямоугольников [2 стр. 479]:
– левых прямоугольников;
– правых прямоугольников;
– средних прямоугольников.
Формула вычисления интегралов с помощью левых прямоугольников представлена записью 1.2.

Графическое представление вычисления интегралов с помощью левых прямоугольников представлено на рисунке 1.2.

Рисунок 1.2 – Геометрическое изображение интеграла в виде суммы
«левых» прямоугольников
Формула вычисления интегралов с помощью правых прямоугольников представлена записью 1.3.

Графическое представление вычисления интегралов с помощью правых прямоугольников представлено на рисунке 1.3.

Рисунок 1.3 – Геометрическое изображение интеграла в виде суммы «правых» прямоугольников
Формула вычисления интегралов с помощью средних прямоугольников представлена записью 1.4.

Графическое представление вычисления интегралов с помощью средних прямоугольников представлено на рисунке 1.4.

Рисунок 1.4 – Геометрическое изображение интеграла в виде суммы «средних» прямоугольников
Три формулы вычисления интегралов с помощью прямоугольников можно заменить одной:

где если b = a, то это формула левых прямоугольников;
если b = a + h, то это формула правых прямоугольников;
если b = a + h/2, то это формула средних прямоугольников;
где h – шаг, равный (a + b)/2; n – количество прямоугольников.
1.3.2 Формула трапеций
«Верхняя» часть элементарного фрагмента суммы интеграла заменяется прямой линией – получаемая геометрическая фигура является трапецией. Формула вычисления интегралов в виде сумм трапеций представлена записью 1.6.

Графическое представление вычисления интегралов с помощью сумм трапеций представлено на рисунке 1.5.
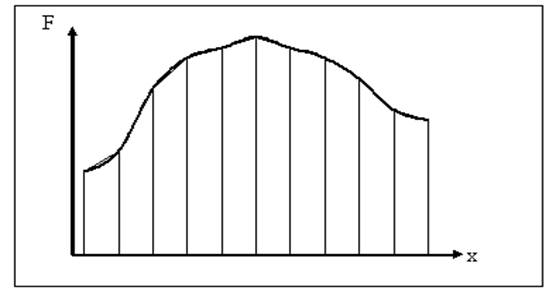
Рисунок 1.5 – Геометрическое изображение интеграла в виде сумм трапеций
1.3.3 Формула Симпсона (параболических трапеций)
«Верхняя» часть элементарного фрагмента суммы интеграла заменяется отрезком параболы. Формула вычисления интегралов в виде сумм парабол трапеций представлена записью 1.7.

где h – шаг, равный (b - a)/2; n – четное число.
Графическое представление вычисления интегралов с помощью сумм парабол трапеций представлено на рисунке 1.6.

Рисунок 1.6 – Геометрическое изображение интеграла в виде сумм
парабол трапеций
Варианты индивидуальных заданий
Интегральная функция и численный метод вычисления интеграла выбираются из нижеследующей таблицы 1.1.
Таблица 1.1 – Варианты заданий
| Метод \ Функция | S1 | S2 | S3 | S4 |
| Правых прямоугольников | 1 вар. | 2 вар. | 3 вар. | 4 вар. |
| Левых прямоугольников | 5 вар. | 6 вар. | 7 вар. | 8 вар. |
| Средних прямоугольников | 9 вар. | 10 вар. | 11 вар. | 12 вар. |
| Трапеций | 13 вар. | 14 вар. | 15 вар. | 16 вар. |
| Симпсона | 17 вар. | 18 вар. | 19 вар. | 20 вар. |
где:

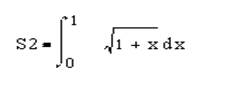


Тема 2 ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ НА РАЗРАБОТКУ WINDOWS-ПРИЛОЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ ТЕОРИИ ГРАФОВ.
Date: 2016-06-06; view: 712; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |