Основные определения. Нечеткие системы управления (НСУ) относятся к классу интеллек­туаль­ных систем управления

НЕЧЕТКИЕ МНОЖЕСТВА

Нечеткие системы управления (НСУ) относятся к классу интеллек­туаль­ных систем управления. Теория нечетких систем управления - единствен­ная, которая математически оперирует со смысловым содер­жанием слов че­ловека, дает возможность наилучшим образом структу­рировать все то, что разделено не очень точными границами (например, мысль, язык, восприятие чего-либо людьми), позволяет создать аппарат, способ­ный моделировать рассуждения человека, объяснять приемы принятия решений в ходе рассмотрения различ­ных прикладных задач.

НСУ применяются, чтобы повысить эффективность функциони­рования регуляторов в условиях:

1) неопределенности информации о динамическом поведении слож­ных объектов управления;

2) неопределенности информации о внешней среде;

3) неопределенности целей управления (необходимость учитывать раз­личные цели).

Впервые НСУ применены в 80-х гг. в Дании на цементном за­воде для мо­делирования поведения человека-опера­тора; в 1987 г. введена НСУ движе­нием поездов метрополитена в Японии; бортовая НСУ использована в кос­мическом летательном аппарате типа "Шаттл". К настоящему времени НСУ заняли ведущую роль в разработке экс­пертных систем, в компьютерных сис­темах искусственного интеллекта: для распо­знавания изображений и речи; в меди­цине при диагностике; для прогнозиро­вания по­годы, предсказания зем­летрясений; в экономике для прогнозирова­ния и принятия решений; в промыш­ленности - в робототехнике, при управ­лении технологическими процессами, диагностике неисправностей, анализе надежности; в ком­пьютерной технике применяются нечеткие процессоры, так называе­мые нечеткие компьютеры [1]-[5]. Построение НСУ основано на теории нечетких множеств (НМ) (fuzzy sets), разработанной в 1965 г. профессором Кали­форнийского университета Л. А. Заде [6].

Основные определения

Отличие НМ от четких (обычных) в том, что в НМ степень принад­леж­но­сти элемента множеству может быть любым числом единичного интер­вала , а не только одним из двух значений , как в случае четкого множе­ства, т. е. учитывается возможность постепенного пере­хода от при­надлежно­сти к непринадлежности элемента множеству [1]-[3], [6]-[9]. Основные определе­ния четких множеств приведены в прил. 1.

Вводится специальная характеристическая функция (см. прил. 1) - так на­зывае­мая функция принадлежности (ФП) , определяющая нечет­кое под­множество А в универсальном множестве U. ФП представляет собой отобра­жение, для кото­рого U - область определения, а интервал [0, 1] есть область значений ® .

Примерами нечетких множеств могут служить следующие.

· Нижняя граница "горячо" температуры в водяном котле находится около 80° С. Теория четких множеств относит любую температуру, равную или большую 80°, к множеству "горячо" - А (четкому множеству), но не включает в него темпера­туры ниже 80°. Поэтому вода с температурой 80.001° считается горячей, а 79.999° - нет (рис. 1.1, t Î U).

Такой способ различения температур не

совпадает с опытом и мышлением человека.

В соответствии с теорией нечетких множеств

температуру 79.999° можно, например, отнести

к множеству "горячо" - А (НМ) на 99%,

температуру 70° - на 80% и т. д.

· В заданном множестве людей может быть подмножество высоких лю­дей.

· В множестве цветов выделяется подмножество темно-зеленых цветов.

· Пусть а - действительное число, u - небольшое положительное при­раще­ние а, тогда а + u образуют нечеткое подмножество в множестве действи­тельных чисел.

НМ определяется математически как совокупность упорядочен­ных пар, составленных из элементов u универсального множества U и соответ­ствую­щих степеней принадлежности . НМ яв­ляется подмноже­ством универсального множества U, т. е. .

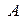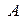Функция принадлежности ставит в соответствие каждому элементу число из интервала [0, 1], характеризующее степень при­надлежности элемента нечеткому множеству . Величина оз­начает субъективную оценку степени принадлежности мно­же­ству (например, (, рис. 1.1) означает, что на 80% принад­лежит множе­ству ).

Поскольку ФП является исчерпывающей характери­стикой НМ, часто ото­ждествляют НМ и его функцию принадлежности [8].

Замечание. Два значения характеристической функции четкого множества (см. прил. 1) принадлежат замкну­тому интервалу , следова­тельно, четкое множество является частным случаем НМ.

Нечетким синглтоном называется одноточечное НМ , Î (0, 1].

Варианты записи НМ:

;

A =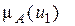

.

Здесь знак "+" обозначает объединение, а не арифметическое суммирова­ние [6], и поэтому данную запись можно рассматривать как представление НМ А в виде объединения составляющих его одноточечных множеств нечетких синглтонов.

Пример 1.1: , и т. д.;

u 1 u 2 u 3 u 4

А =

0.2

0.6

0.8

.

Представление НМ с помощью

графика ФП показано на рис.1.1.

Графическая иллюстрация НМ

с помощью концентрических линий

дана на диаграмме Венна-Эйлера

(рис. 1.2).

Четкое множество А, ближайшее к нечеткому А (т. е. расположенное на наименьшем линейном или евклидовом расстоянии (см. прил. 1) от данного нечеткого множества), характеризуется ФП

(1.1)

Примем

u ₁ u ₂ u ₃ u ₄ u ₅ u ₆ u ₇ u ₈

u ₁ u ₂ u ₃ u ₄ u ₅ u ₆ u ₇ u ₈

Объединение всех НМ универсального множества U обозначим R (U). Пусть L - множество значений ФП, Ì 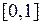. Пусть кардинальные числа 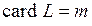. Тогда карди­нальное число степенного (четкого) множе­ства (см. прил. 1) а кардинальное число объе­динения НМ

. (1.2)

Пример 1.3:

НМ называется нормальным, если верхняя граница ФП равна 1: ; в противном случае НМ называется субнормальным. Не­пус­тое субнормальное множество можно привести (нор­ма­лизо­вать) к нормальному по формуле

. (1.3)